Практичні завдання

1) Визначення ринкової вартості купонної облігації

. (1)

де С – щорічна сума відсотка за облігацією (опорна виплата, купонні виплати);

N – сума, яку отримує власник облігації при її погашенні (як правило, дорівнює номінальній вартості облігації);

n – кількість років (періодів) до погашення;

i – порядковий номер періодів;

k₀ – ставка дисконтування, що дорівнює існуючій ставці за подібними зобов’язаннями та відображає дохідність при погашенні цієї облігації.

Формулу (1) використовують для оцінювання ринкової вартості облігації у разі, коли останні купонні виплати щойно відбулися, а на­ступні будуть здійснені в кінці періоду (якщо виплати проводять щороку, наступні виплати мають відбутися через рік).

Якщо з моменту останніх купонних виплат минуло t₁ днів, до на­ступних виплат залишилося t днів, період становить Т днів (як пра­вило, Т = 365), вартість облігації з фіксованим купоном С з достатнім ступенем точності може бути обчислена за формулою

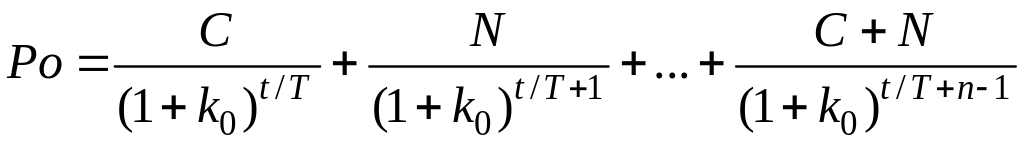. (2)

або

. (3)

При цьому ціна, яку повинен сплатити інвестор власнику облігації при її купівлі, має бути більшою від Р₀ на величину накопиченого процента I, що утворився за період з останньої виплати процентів до даного моменту, тобто за період t₁ = Т – t :

. (4)

Накопичений процент I розраховують за формулою

. (5)

Приклад 1. Облігація з фіксованим купоном 11%, що сплачується раз на рік, буде погашена 01.12.06 р. за номінальною вартістю 1000 гр. од. Оцінити ринкову вартість облігації після сплати за нею про­центів 01.12.02 р., якщо дохідність к₀ подібних облігацій, що перебу­вають в обігу в даний момент на ринку, становить 9%. Наступні ку­понні виплати за облігаціями будуть здійснені через рік.

Очікувані грошові потоки за цією облігації складаються з чоти­рикратних купонних виплат у розмірі 110 гр. од. та суми 1000 гр. од., яку отримає власник облігації 01.12.06 р. при її погашенні.

110 гр. од. 110 гр. од. 110 гр. од. 1110 гр. од.

І--------I--------I---------------------I--------------------I---------------------I

01.12.02 05.05.03 01.12.03 01.12.04 01.12.05 01.12.06

Для оцінювання ринкової вартості облігації потрібно дисконту­вати грошові потоки на дату 01.12.02 р. за ставкою k₀ = 9%, яка ви­значає дохідність подібних облігацій, тобто:

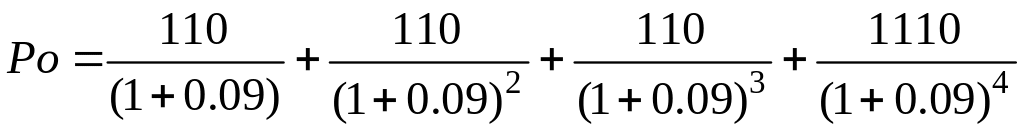= 1064,79 гр. од.

При k₀ = 9% ринкова вартість облігації становить 1064,79 гр. од.

Приклад 2. Облігація з фіксованим купоном 11%, що сплачується раз на рік, буде погашена 01.12.06 р. за номінальною вартістю 1000 гр. од. Яку суму повинен сплатити інвестор власнику облігації при купівлі її 05.05.03 р., якщо останні купонні виплати відбулися 01.12.02 р., ринкова дохідність подібних облігацій, що перебувають в обігу в цей момент на ринку, становить 12%?

Для того щоб визначити ціну продажу облігації на ринку 05.05.03 р., коли з моменту останніх купонних виплат минуло 155 днів, а до наступних виплат залишилося 210 днів, треба розрахувати теперішню вартість очікуваних грошових потоків за облігаціями за формулою (3) та обчислити накопичений власником облігації за 155 днів процент І:

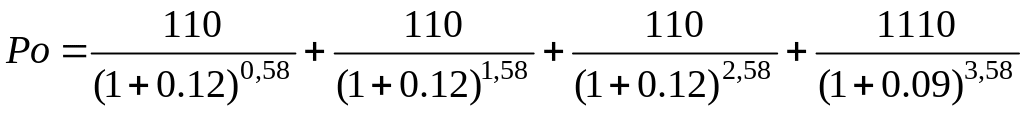
Р₀= 970,74 гр. од.;

За формулою (5)

І = 110 • 155 : 365 = 46,71 гр. од.

Придбати таку облігацію на ринку можна згідно з (4) за ціною

Р^*₀ = 970,74 + 46,71 = 1017,45 гр. од., що компенсує її попередньому власнику втрати від володіння облігацією протягом 155 днів без можливості отримати наступні купонні виплати.

Приклад 3. Облігація з фіксованим купоном 11%, що сплачується раз на рік, буде погашена 01.12.06 р. за номінальною вартістю 1000 гр. од. Яку дохідність забезпечить облігація інвестору, якщо вона при­дбана 01.12.02 р. після сплати за нею процентів за ринковою ціною 980 гр. од.?

Для визначення очікуваної дохідності облігації при відомій її ринковій вартості слід розв'язати рівняння 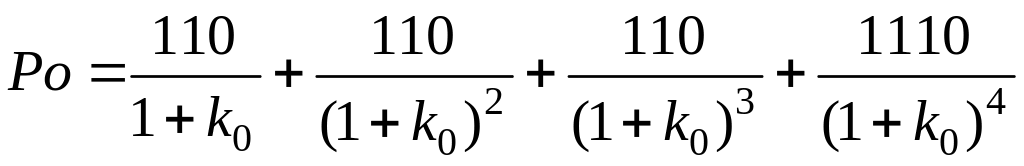відносно k₀, тобто

Рівняння такого типу мають аналітичний розв'язок лише в окре­мих випадках. Наведене рівняння розв'язується за допомогою фінан­сового калькулятора або комп'ютера. Розв'язком рівняння є процент­на ставка k₀ = 0,1165, або k₀=11,65%. Якщо інвестор придбає обліга­цію 01.12.02 р. після сплати по ній процентів за ціною 980 гр. од., вона забезпечить йому дохідність на рівні 11,65%, що на 0,65% вище від купонної ставки.

Приклад 4. Облігація з фіксованим купоном 11%, що сплачується раз на рік, буде погашена 01.12.06 р. за номінальною вартістю 1000 гр. од. Чи забезпечить ця облігація інвестору дохідність на рівні 11,5%, якщо придбати її за ринковою ціною 990 гр. од. 01.12.02 р. після сплати за нею процентів?

Для того щоб визначити, чи забезпечить ця облігація інвестору дохідність на рівні 11,5%, якщо придбати її за ринковою вартістю 990 гр. од. 01.12.02 р. після сплати за нею процентів, необхідно роз­в'язати відносно k₀ рівняння:

Розв'язком рівняння є k₀ = 11,32%. Це означає, що придбання облігації 01.12.02 р. після сплати за нею процентів за ціною 990 гр. од. забезпечить власнику при погашенні облігації 01.12.06 р. дохідність у розмірі 11,32%, що на 0,18% менше від необхідної ставки доходу 11,5%. Підставляючи k₀ = 11,5%, можна визначити, що рин­кова вартість, яка становить Р₀= 984,65 гр. од., забезпечить необ­хідну ставку доходу в розмірі 11,5%.