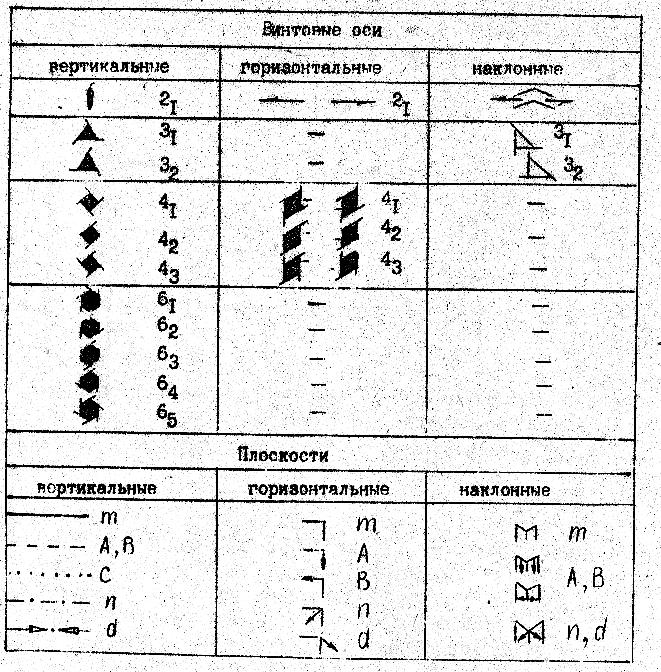
Международные обозначения винтовых осей и плоскостей скользящего отражения.

3.10. Координационное число. Координационный многогранник

Координационным числом (к.ч.) данного атома (иона) называется число ближайших соседних атомов (ионов). Если центры этих ближайших атомов или ионов мысленно соединить друг с другом прямыми линиями, то в общем случае получается координационный многогранник (рис.43).

Рис. 43. Координационные многогранники: а - гантель, к.ч. = 2; б - треугольник, к.ч. = 3; в - тетраэдрр, к.ч. = 4; г - октаэдр, к.ч. = 6; д - куб, к.ч. = 8; е - кубооктаэдр, к.ч. = 12

Ионы могут быть отрицательно заряженными (анион) и положительно заряженными (катион).

При изучении структуры кристалла обращают внимание на расстояние между структурными единицами (ионами, атомами). В связи с этим важно установить те минимально допустимые расстояния, на которые могут приблизиться друг к другу две такие структурные единицы. С этой целью мысленно каждому атому или иону присваивают некоторую сферу действия, внутрь которой никакие другие атомы или ионы проникать не могут. Такая сфера действия называется атомной или ионной, а ее радиус – атомным или ионным эффективным радиусом (не смешивать эффективный радиус с расстоянием наружной электронной оболочки атома (или иона) от ядра).

Теоретически рассчитаны для каждого координационного многогранника те отношения радиуса центрального атома (иона) к радиусу оркужающих атомов (ионов), в пределах которых структура должна еще обладать устойчивостью (если структура не устойчива, то происходит ее перестройка до более устойчивой с иным координационным числом).

Ниже приводятся пределы отношений r_а/r_х (r_а- радиус катиона, r_х- радиус аниона), при которых будут устойчивы структуры с известным координационным число. Примерно, ¾ металлов кристаллизуются в трех почти одинаково часто встречающихся решетках: Г.П.У., Г.Ц.К., О.Ц.К. (гексагональная плотноупакованная, гранецентрированная кубическая, объемоцентрированная кубическая). Остальные обладают решетками примерно 12 различных типов.

Для металлов характерна к.ч.=12 (Г.П.У. и Г.Ц.К. решетки) и к.ч.=8 (О.Ц.К.решетка).

Таблица 6

Координационное число для некоторых структур

Координационное число	координационные многогранники	Примеры структур	ra/rx
			От	до
2	гантель		0	0,115
3	треугольник		0,115	0,225
4	тетраэдр	ZnS,алмаз	0,225	0,414
6	октаэдр	NaCL	0,414	0,732
8	куб (гексаэдр)	W,Mo,Nb,Ta	0,732	1,000
12	кубооктаэдр	медь и многие металлы	1,00

Вопросы для самопроверки:

1. Дайте определение центра инверсии.

2. Дайте определение оси симметрии.

3. Дайте определение плоскости симметрии.

4. Объясните, что такое инверсионная ось симметрии.

5. Дайте определение понятия элементарного угла поворота.

6. Дайте понятие порядка оси симметрии.

7. Укажите, каких порядков бывают оси симметрии, и каким углам поворота

они соответствуют.

8. Объясните, почему не существует осей симметрии 5-го порядка и выше шестого.

9. Укажите возможное число существующих осей симметрии в конечной

фигуре.

10. Объясните, какую фигуру называют конечной.

11. Укажите, каким элементам симметрии равносильны инверсионные оси

порядков 1, 2, 3, 4, 6.

12. Зарисуйте, как обозначают элементы симметрии конечных фигур на плоскости стереографической проекции.

13. Объясните, что такое теоремы сложения и для чего их применяют.

14. Укажите, какое направление называют единичными.

15. Дайте определение симметрично-равного направления.

16. Объясните что такое категория кристаллов.

17. Объясните, что такое сингония.

18. Укажите, какие различают сингонии.

19. Укажите, на какие категории делятся кристаллы.

20. Объясните, что такое кристаллографическая формула.

21. Укажите, как записывают кристаллографическую формулу по элементам

симметрии.

22. Объясните, что такое класс симметрии кристаллов.

23. Укажите, что такое простая форма кристаллов.

24. Зарисуйте примеры открытых и закрытых форм кристаллов.

25. Дайте определение кристаллической решетки.

26. Дайте определение ячейки (решетки) Бравэ.

27. Укажите, какими параметрами характеризуется решетка Бравэ.

28. Объясните, что такое сингония.

29. Запишите правила выбора ячейки Бравэ.

30. Укажите, на какие типы подразделяются ячейки Бравэ.

31. Дайте определение базиса кристаллической ячейки и правила его записи.

32. Зарисуйте базоцентрированную ячейку Бравэ и укажите ее базис.

33. Зарисуйте ячейку ГЦК и запишите ее базис.

34. Зарисуйте ячейку ОЦК и запишите ее базис.

35. Укажите отличия в элементах симметрии конечных фигур и бесконечных.

36. Дайте определение бесконечной фигуры.

37. Укажите, чем отличаются плоскости скользящего отражения от зеркаль

ной плоскости симметрии.

38. Укажите, чем отличаются плоскости типов “А”, “В”, “С”.

39. Объясните, чем отличаются плоскости типов “n” и “d”.

40. Запишите, для каких типов решетки характерны плоскости скользящего

отражения типов “n” и “d”.

41. Объясните чем отличается винтовая ось симметрии от поворотной.

42. Объясните чем отличается инверсионная ось симметрии от поворотной.

43. Укажите отличия правой и левой винтовых осей симметрии.

44. Запишите обозначения винтовых осей симметрии.

45. Дайте определение “хода”, (“шага”, “элементарной трансляции”) винто

вой оси симметрии.

46. Запишите обозначения винтовых осей, плоскостей симметрии в Между

народной системе.

47. Дайте понятие пространственной группы симметрии.

48. Дайте понятие точечной группы симметрии.

49. Запишите обозначение символов пространственных групп симметрии в

Международной системе.

50. Дайте определение координационного числа, координационного много-

гранника.

51. Зарисуйте простые координационные многогранники.

52. Дайте определение атомного (ионного) эффективного радиуса.

53. Дайте определение стехиометрической формулы вещества.

54. Укажите, какая часть атома приходится на долю элементарной ячейки, если он находится в вершине ячейки.