3.5.Категории и сингонии
Полное сочетание элементов симметрии кристаллического многогранника называется его классом симметрии или точечной группой симметрии. Существует 32 класса симметрии кристаллов. Учитывая особенности сочетаний элементов симметрии, 32 класса симметрии делятся на три категории. В кристаллических многогранниках встречаются единичные или симметрично – равные направления.
Единичным направлением называется единственное, не повторяющееся в кристаллическом многограннике направление. Таковым является, например, направление, совпадающее с осью L6 в шестигранной пирамиде.
Симметрично-равное направление, которое можно получить с помощью элементов симметрии, и которому есть равное в кристаллическом многограннике.
В кубе нет единичных направлений, здесь для любого направления можно найти симметрично-равное.
По симметрии и по числу единичных направлений кристаллы делятся на три категории: низшую, среднюю, высшую.
К низшей категории относятся кристаллы, у которых нет осей симметрии выше второго порядка и есть несколько единичных направлений. Это кристаллы наименее симметричные, с ярко выраженной анизотропией свойств.
К средней категории относятся кристаллы, у которых имеется главная ось (главной осью симметрии называется простая ось симметрии, или инверсионная ось, совпадающая с единственным единичным направлением) порядка выше второго (и она одна) и есть одно единичное направление, совпадающее с главной осью. В кристаллах средней категории заметно различие свойств вдоль и поперек оси симметрии. Характерные формы кристаллов, относящихся к средней категории-призмы, пирамиды и др.
Кристаллы вышей категории имеют несколько осей симметрии порядка выше второго, и единичных направлений в них нет; все направления являются симметрично-равными, поэтому анизотропия свойств в кристаллах высшей категории выражена слабее всего. Примерами кристаллов, относящихся к высшей категории, являются куб, октаэдр, тетраэдр.
Все 32 класса симметрии кристаллов разделяются по трем категориям, которые в свою очередь, разделяются на 7 сингоний.
Таблица 3
Характеристика категорий и сингоний
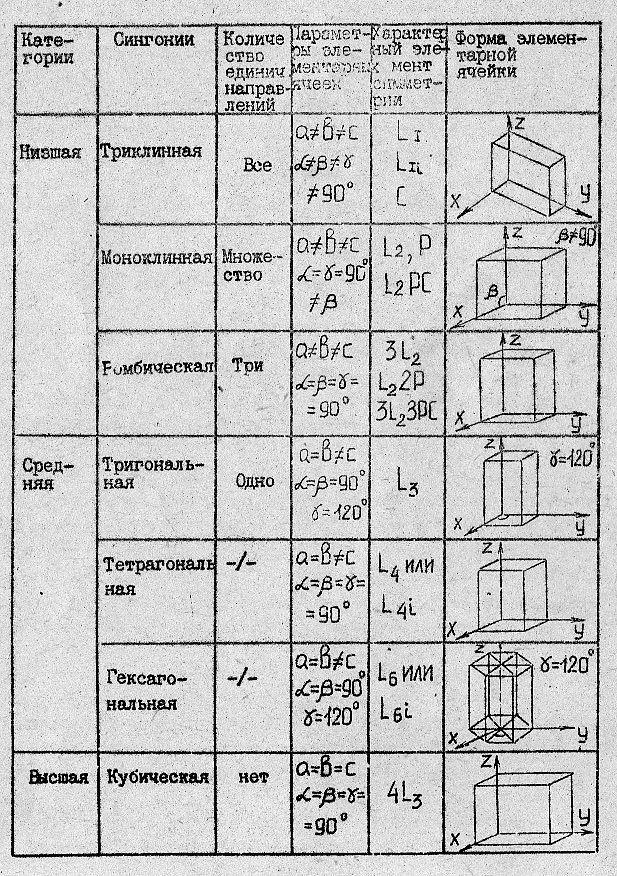
(понятие, введенное французским ученым Ш. Сорэ в 1893 г.) В сингонии объединяются те кристаллы, для которых одинакова симметрия элементарных ячеек их структур и одинакова система осей координат. Кристаллам, принадлежащим к классам одной сингонии, свойственна совокупность характерных углов. Отсюда и название «сингония», буквально означающее «сходноугольность» (в переводе с греческого).
Классификация кристаллов по сингониям определяется выбором кристаллографической системы координат, или элементарной ячейки кристалла. Характеристика категорий и сингоний кристаллов дана в табл.3.
Для того, чтобы разные исследователи могли описывать кристаллы одинаковыми символами, введены правила кристаллографической установки – условный порядок расположения осей координат. Правила установки кристаллов показаны в табл.3.