3. Проецирование точки

3.1. Проецирование точки на две и три плоскости проекций

Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций П₁ и П₂, опустить из нее перпендикуляры на эти плоскости, получают проекции точки А - А₁ и А₂, которые являются ортогональными проекциями относительно плоскостей про­екций П₁, и П₂. Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы. Так, для точки А:

[A A₁]=[A₂A_x]=z_A;

[AA₂]=[A₁ A_x]=y_A.

Плоскость прямоугольника А₁АА₂А_x, перпендикулярна к: оси x, а линии пересечений плоскостей П₁П₂ и плоскости А₁АА₂А_x являются прямыми А₁А_x и А₂А_x, перпендикулярными к оси х. Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.

Чтобы получить плоский чертёж, поворачивают плоскость П₁, вокруг оси х и совмещают её с плоскостью П₂ (рис. 3.1), получая таким образом. комплексный чертеж (эпюр Монжа)

Рис. 3.1	Рис. 3.2

Проекции а₁ и А₂ оказываются на одной линии, которая называется линией проекционной связи. Она перпендикулярна к оси х (рис. 3.2).

При проецировании точки А на три плоскости проекций от плоскости П₃ она отстоит на расстоянии АА₃ (рис. 3.3). При этом, аналогично вышесказанному:

[АА₃]=[0А_х]=x_А;

[A₃A_z]=[AA₂]=[0A_Y]=y_A;

[A₃A_y]=[AA₁]=0A_Z]= z_a.

Для получения плоского чертежа в этом случае уже две плоскости П₁ и П₃ совмещаются с плоскостью П₂ путём поворота их соответственно вокруг осей х и z. При этом ось у как бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показано на рис. 3.3. Профильная проекция А₃ точки А находится на пересечении линий связи A₂A_ZA₃ и A₁AуA₃ (расстояние 0Ау=0Ау). Перенос точки Ау в точку (Aу) - понятен из чертежа, а сам отрезок есть не что иное, как координата y_a.

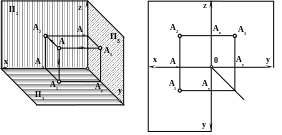
Рис. 3.3

На плоском трёхмерном чертеже положительное направление оси х совпадает с отрицательным направлением оси у, а отрицательное направление оси y - с положительным направлением оси z.

z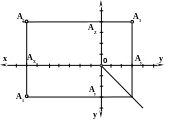

Pис. 3.4

Это не означает, что модули этих величин обязательно равны между собой, т.е. (в частном случае это равенство может быть). Те же рассуждения будут справедливы и в отношении направлений осей z и y (рис. 3.4).

Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.

2. Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства

Точка, например А, принадлежит:

• I или V октанту, если её проекция А₁(лежит под осью х, а А₂ - над осью х;

• II или VI октанту, если и А₁ и А₂ лежат над осью х;

• III или VII октанту, если A₁ лежит над осью х, а А₂ - под осью х;

• IV или VIII октанту, если и А₁ и А₂ лежат под осью х.