
- •1.Классификация дифференциальных уравнений с частными производными
- •1.1 Основные дифференциальные уравнения математической физики
- •2.Классификация уравнений с частными производными второго порядка
- •2.1.Дифференциальное уравнение с двумя неизвестными переменными
- •2.2.Приведение уравнений к каноническому виду Приведение к каноническому виду уравнения гиперболического типа
- •Приведение к каноническому виду уравнения параболического типа
- •Приведение к каноническому виду уравнения эллиптического типа
- •2.3.Канонические формы линейных уравнений с постоянными коэффициентами
- •Уравнение для продольных колебаний струны.
- •Энергия колебаний струны
- •Малые поперечные колебания мембраны
- •3.2.Уравнение для напряженности электрического и магнитного полей в вакууме
- •Уравнение для скалярного статического поля
- •Граничные и начальные условия
- •Поперечные колебания струны закрепленной на концах
- •4.Метод разделения переменных (метод Фурье)
- •4.1.Интерпретация решения
- •4.2.Неоднородные уравнения колебаний
- •4.3.Общая первая краевая задача
- •4.4.Общая схема метода разделения переменных
4.3.Общая первая краевая задача
Постановка общей первой краевой задачи для уравнений колебания ставится следующем образом. Найдем решение уравнения (1):
где ,
С дополнительными условиями:
, ,
![]() ,
,
![]() ,
,
![]() (2)
(2)
Сведем исходную
задачу к более простой. Будем искать
решение
![]() в виде
в виде
![]() (3)
(3)
Тогда уравнение примет вид
![]()
Где
![]()
С дополнительными условиями
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
Последнее два
выражения дают связь между граничными
значениями функций
![]() и
и
![]() .
Если выбрать функцию
таки
образом, чтобы
.
Если выбрать функцию
таки
образом, чтобы
![]() и
и
![]() ,
то задача для нахождения функции
сведется к уже решенной в предыдущем
пункте задаче для неоднородного уравнения
с нулевыми граничными условиями. Легко
видеть, что для выполнения
и
достаточно положить
,
то задача для нахождения функции
сведется к уже решенной в предыдущем
пункте задаче для неоднородного уравнения
с нулевыми граничными условиями. Легко
видеть, что для выполнения
и
достаточно положить
![]()
![]()
![]()
![]()
![]() ,
,
![]()
4.4.Общая схема метода разделения переменных
Данная схема применяется не только к колебаниям однородной струны, но и к колебаниям неоднородным колебаниям струны.
![]() (1)
(1)
Где ,
, , (2)
,
,
,
![]() ,
,
![]() ,
,
![]() (3)
(3)
Для отыскания решения обратимся к вспомогательной задачи. Найдем нетривиальное решение уравнения (1) удовлетворяющее граничным условиям (2) и представимое в виде
(4)
Подставляем (4) в (1), получаем
![]()
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Если воспользоваться решением уравнения (4), то получим
![]()
Это есть дополнительные условия.
Найдем те значения параметра , при которых существует нетривиальное решение задачи (7). Такие значения параметра называются собственными значениями, а соответственно им нетривиальное решение – собственными функциями.
Основные свойства:
1.Существует бесконечное множество собственных значения, которые соответствуют нетривиальному решению.
2.Все собственные значения вещественные, а при они положительные.
3.Собственные
значения
![]() принимают
соотношения различных значений
принимают
соотношения различных значений
![]() ортогональные
между собой с весом
ортогональные
между собой с весом
![]() на
отрезке
.
на
отрезке
.
![]() (8)
(8)
4.Теорема разложения Стеклова
Пусть дана функция
F(x)
дважды непрерывная дифференцируемая
и удовлетворяющая нулевым граничным
условиям ![]() .
Данная функция разлагается в равномерный
и абсолютно сходящийся ряд.
.
Данная функция разлагается в равномерный
и абсолютно сходящийся ряд.
![]() (9)
(9)
![]()
![]()
![]()
Свойства (1) и (4)
основаны на теории интегральных
уравнений. Остановимся на доказательстве
свойств (2) и (3). Для этого выберем формулу
Грина. Пусть есть
![]() и
и
![]() произвольные и дважды дифференцируемые
на отрезке
произвольные и дважды дифференцируемые
на отрезке![]() .
.
![]()
![]()
![]() (10)
(10)
Докажем (3) свойство.
Пусть
![]() и
и
![]() две собственных
функций собственных значений
две собственных
функций собственных значений
![]() и
и
![]() .
.
![]()
![]()
Учитывая граничные условия
![]() ,
,
![]()
![]()
Воспользуемся соотношением
![]()
Получим:
![]()
За счет граничных условий правая часть в формуле Грина обратится в ноль. Таким образом доказали формулу (8), т.е. получили:
![]()
![]() (11)
(11)
Это доказательство
того что каждому собственному значению
соответствует только одна собственная
функция. Функции, которые отличаются
друг от друга на множитель, мы различать
не будем. В силу линейности и однородности
уравнения (7) и граничными условиями
ясно следующее, если
является собственной функцией отвечающей
собственных значений
,
то и функция
![]() ,
где
,
где
![]() -
произвольная константа. Чтобы избежать
неопределенности в выборе множителя
подчиним условию нормировки:
-
произвольная константа. Чтобы избежать
неопределенности в выборе множителя
подчиним условию нормировки:
![]()
Если
![]() не
удовлетворяет условию нормировке, тогда
домножаем ее на число
и
уже требуем выполнения условия
не
удовлетворяет условию нормировке, тогда
домножаем ее на число
и
уже требуем выполнения условия
![]()
![]()
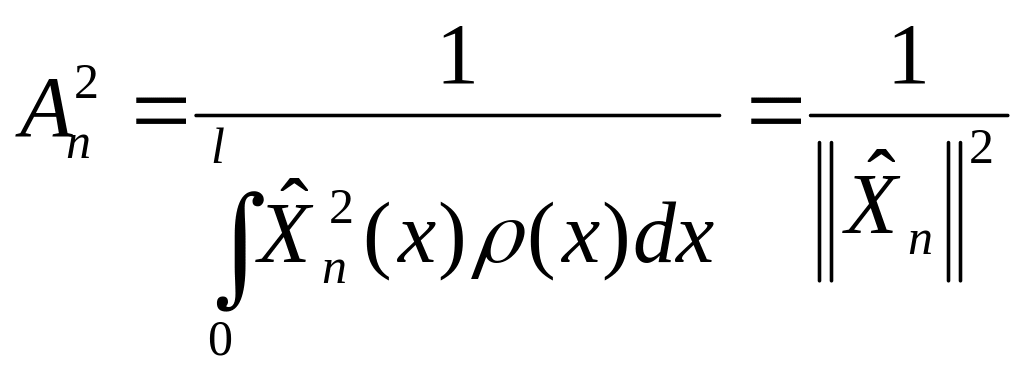
![]()
Если подчинить задачу (7) условию нормировки, то тогда общее соотношение будет записано в виде:
![]()
Это условие ортогональности.
Докажем свойство (2).
Пусть собственные
значения
являются комплексными:
![]() ,
,
![]() ему будет
соответствовать
ему будет
соответствовать
![]() следовательно, функция является
комплексной. Из граничных условий
следовательно, функция является
комплексной. Из граничных условий
![]() следует, что
следует, что
![]() ,
,
![]() .
Подставим собственные значения и
собственную функцию в (7), получим:
.
Подставим собственные значения и
собственную функцию в (7), получим:
![]()
Возьмем комплексное сопряжение
![]()
![]()
![]()
![]()
Собственные значения разные, следовательно, функции разные. Это значит, что интеграл равен нулю.
![]()
Пусть
![]()
![]()
![]()
![]()
Числа
![]()
Запишем
разложение
![]() в ряд
в ряд
![]()
![]()
Все что мы делали,
касалось функции
![]() .
Теперь рассмотрим для Функции
.
.
Теперь рассмотрим для Функции
.
![]() и
и
![]() неизвестны.
неизвестны.
Вспомогательная задача имеет решение в виде:
![]()
Просуммируем и получим общее решение
![]()
![]()
![]()
![]()
![]()
Не следует считать, что общая схема применяется для первой и второй краевой задачи. Общую схему можно применить и для третий краевой задачи, которая является обобщением первой и второй краевых задач.
Третья краевая задача.
Найдем решение уравнения
![]() ,
,
![]() (1)
(1)
![]() - функции непрерывны
на промежутке
- функции непрерывны
на промежутке
![]()
Начальные условия:
![]() ,
,
![]() (2)
(2)
Граничные условия:
![]() (3)
(3)
![]()
Соотношения между ними
![]()
Зададим решение методом разделения переменных. Следовательно, будем искать решение в виде произведений, и данное решение подставим в уравнение (1).
![]()
![]() (4)
(4)
Из уравнения (4),
если
![]() ,
мы получим первую краевую задачу. При
,
мы получим первую краевую задачу. При
![]() получим вторую краевую задачу, треть
краевая задача является линейной
комбинацией.
получим вторую краевую задачу, треть
краевая задача является линейной
комбинацией.
Используя значение функций и собственные значения можно преступить к решению неоднородного уравнения в случае однородных граничных условий третий краевой задачи.
