14.Определение оптимального расстояния между вершинами ациклического графа.
Направленный ациклический граф — случай направленного графа, в котором отсутствуют направленные циклы, то есть пути, начинающиеся и кончающиеся в одной и той же вершине. Направленный ациклический граф является обобщением дерева (точнее, их объединения — леса).
Оптимизация
DAWG (англ. directed acyclic word graph) — компактная форма хранения префиксного дерева, списка слов, оптимизированная для выяснения, входит ли некое слово в данный список или нет. Сам список получить несложно рекурсивным обходом дерева. С точки зрения программы, осуществляющей обход или поиск, DAWG ничем не отличается от дерева, просто одинаковые поддеревья хранятся в единственном экземпляре.
Сам способ преобразования очевиден: поиск одинаковых поддеревьев и переподключение ссылок на единственный экземпляр. На самом деле помимо буквы в вершинах хранится флажок, указывающий, является ли данная буква последней. Так что для списков неповторяющихся слов преобразование в DAWG и обратно происходит без потерь
19.Метод составления по заданному чертежу графа матрицы инциденций,смежности,фундаментальных циклов,фундаментальных разрезов..
Матрица инциденций – это матрица размера n m, где n – число вершин, а m – число ребер графа, при этом ее элементы kij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.
20.Составления списка хорд и ветвей графа по заданной матрице инциденций.
17.Метод расстановки пометок для решения задачи о максимальном потоке.Алгоритм Фалкерсона.
Аппроксимация функций и ее использование в компьютерном проектировании
Аппроксимация - заданное представление некоторой неизвестной функции в виде разложения по известным функциям.
В понятие аппроксимации входит решение как прямой, так и обратной задачи.
Конечная цель решения задачи аппроксимации - нахождения коэффициент аппроксимации, которые представляет собой численную модель неизвестной функции, в какой-то системе компьютерных моделей.
Пример: В примере OPAL* коэффициенты аберрации представляет собой численную модель волновой аберрации (основой волновой аберрационной функции является эйконал*) в системе моделей оптической системы.
Численная модель требуется для получения значения функции в любой точке. Это используется, когда непосредственно получить очень долго, либо невозможно.
Пример: Производится измерения волновой аберрации ОС* Установка позволяет производить измерения в каких-то определенных точках, с помощью же аппроксимации получает значение в любой точке.
Сами коэффициенты аппроксимации является иллюстрацией свойств функций, необходимых для исследователя.
Существую две проблемы аппроксимации.
1Выбор базисных функций для аппроксимации.
2Выбор узлов аппроксимации.
Цель:
1.Понизить обусловленность задачи.
2.Обеспечить адекватность написания функции.
Мы должны описать функцию так, чтобы характеризуемый ее под процесс был описан правильно. (Направления, волнового процесс нельзя разложить по алгоритму значение аргумента функции. Процесс, имеющий частые колебания, нельзя разложить по колебаниям значение аргумента функции)
3.Простота и минимум вычислений.
4.Линейность.
Нужно стремиться, чтобы между вектором значение аргумента функции и вектором коэффициентов коэффициентa аппроксимации, была зависимость как можно близкая к линейной. Небольшие изменения в векторе значение аргумента функции должно приводить к большим изменениям коэффициентов коэффициентa аппроксимации.
Требования линейности автоматически соблюдается при правильном выборе базиса аппроксимации.
Вычисления и приближение данных в MATLAB
Решение систем линейных алгебраических уравнений и спектральных задач
Решение систем линейных алгебраических уравнений является одной из основных вычислительных задач, поскольку к ней сводятся огромное количество задач, возникающих в самых различных прикладных областях. Численные методы, применяемые для приближенного решения задач механики, для расчета течений жидкостей и газов, других физических процессов в сплошных средах, методы расчета электрических цепей, методы приближения данных приводят к необходимости решения систем линейных алгебраических уравнений (и это далеко не полный перечень источников возникновения линейных алгебраических систем). Спектральные задачи возникают, например, при частотном анализе конструкций, при изучении устойчивости процессов в электрических схемах и системах управления и во многих других прикладных областях.
Обзор возможностей MATLAB для решения систем линейных алгебраических уравнений
Среда MATLAB изначально разрабатывалась для работы с матрицами (MATLAB является сокращением от Matrix Laboratory), поэтому арсенал средств MATLAB для решения систем линейных алгебраических уравнений достаточно богат и включает в себя:
решение систем с квадратными и прямоугольными матрицами;
решение систем прямыми и итерационными (в том числе с возможностью предобусловливания) методами;
матричные разложения;
хранение больших разреженных матриц в компактной форме и специальные алгоритмы для решения систем с такими матрицами.
Решение систем при помощи знака обратной косой черты
Простейшим способом решения систем является применение знака обратной косой черты. Предположим, что требуется решить систему
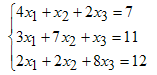
Для этого заполняем матрицу и вектор-столбец правой части (правая часть должна быть именно столбцом, иначе выведется ошибка о несовпадении размерностей)
A = [4 1 2
3 7 1
2 2 8];
f = [7; 11; 12];
и используем знак обратной косой черты
x = A\f
x =
1
1
1
Вместо знака обратной косой черты можно было вызвать функцию mldivide
x = mldivide(A, f)
Результат будет тем же самым
Вычисляя невязку, убеждаемся в том, что решение найдено верно (вообще говоря, не всегда малые значения компонент невязки свидетельствуют о верно найденном решении)
f - A*x
ans =
0
0
0
Очень важно не перепутать местами A и f, т.к. при выполнении операции
x = f\A
никакой ошибки не будет, а выведется
x =
0.2707 0.3439 0.3854
что не имеет ничего общего с решением рассматриваемой системы. Разберем, почему так происходит, записав систему с «матрицей» f и «правой частью» A. Неизвестная при этом будет только одна, т.к. f размера 3 на 1:
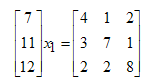
Если в правой части стоит матрица, то решатся столько систем, сколько столбцов у матрицы, при этом каждый столбец является вектором правой части соответствующей системы (т.е. оператор обратной косой черты позволяет решить сразу несколько систем). Итак, решаются системы
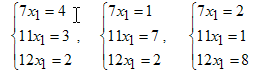
Строго говоря, решения ни у одной из этих систем нет. Однако, если матрица системы прямоугольная и число ее строк больше числа столбцов (т.е. число уравнений больше числа неизвестных), то такая система называется переопределенной (оverdetermined systems) и ее приближенное решение ищется минимизацией евклидовой нормы невязки. Так для первой системы решением будет x , доставляющий минимум следующему выражению
(4-7x1)2+(3-11x1)2+(2-12x1)2
Несложно убедиться, что минимум доставляет
как раз
Воспользуемся, например, средствами
Symbolic Math Toolbox
syms x
R = (7*x-4)^2 + (11*x-3)^2 + (12*x-2)^2
dRdx = diff(R)
x = solve(dRdx)
x =
85/314
double(x)
ans =
0.2707
Итак, полученный при записи x = f\A вектор [0.2707 0.3439 0.3854] содержит решение трех переопределенных систем, правая часть каждой из которых является соответствующим столбцом матрицы A.
Разумеется, матрица переопределенной
системы не обязательно содержит только
один столбец. В качестве примера
рассмотрим задачу о подборе параметров
a и b линейной модели
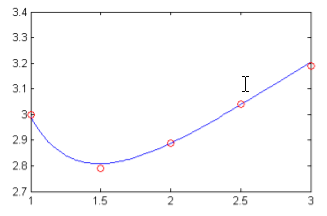
по заданным табличным данным
k 1 2 3 4 5
xk 1.0 1.5 2.0 2.5 3.0
yk 2.99 2.81 2.89 3.03 3.21
Эта задача сводится к переопределенной системе относительно a и b, если мы потребуем равенства y(xk)=yk для k=1,2,...,5:
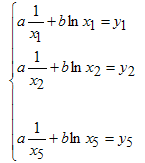
Составляем матрицу системы и вектор правой части
x = (1:0.5:3)'
A = [1./x log(x)];
f = [2.99; 2.81; 2.89; 3.03; 3.21];
и решаем ее
c = A\f
получаем
c =
2.9903
2.0100
т.е. и . График данных и приближения подтверждает правильность полученных результатов
figure
fun = @(x)c(1)/x + c(2)*log(x);
fplot(fun, [1 3])
hold on
plot(x, y, 'or')
Если в системе больше уравнений, чем неизвестных, то такая система называется недоопределенной (underdetermined system) и решается в MATLAB так же при помощи знака обратной косой черты. У нее будет бесконечно много решений и находится решение, содержащее как можно больше нулевых значений. Рассмотрим такой пример
A = [1 2 3 4
5 5 7 8
9 8 7 6];
f = [10; 25; 30];
x = A\f
x =
1.3333
1.0000
0
1.6667
Кроме знака обратной косой черты используется и знак обычной косой черты. Они связаны следующим правилом
B/A эквивалентно (A'\B')'
где апостроф означает транспонирование. Вместо знака обычной косой черты можно использовать также функцию mrdivide.
Пока мы не будем углубляться в алгоритмы решения систем, заложенные в операции обратной косой черты. Этому посвящен раздел Алгоритм решения системы линейных уравнений при помощи знака обратной косой черты. В частности, для решения систем с квадратной матрицей общего вида используется LU-разложение. Кроме того, проверяется обусловленность матрицы. Классическим примером плохо обусловленной матрицы является матрица Гильберта, элементы которой определяются по формуле
Для создания матрицы Гильберта заданного размера в MATLAB служит функция hilb. Решим, например, систему 13-го порядка, правая часть которой такова, что ее решением должны быть все единицы (k-ый элемент правой части есть сумма элементов k-ой строки матрицы).
A = hilb(13);
f = sum(A, 2);
x = A\f
В результате получаем сообщение о плохой обусловленности
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 2.339949e-018.
(RCOND есть оценка для величины, обратной числу обусловленности) и неверное решение
x =
1.0000
1.0000
1.0004
0.9929
1.0636
0.6552
2.2023
-1.7860
5.3352
-3.4773
3.9431
-0.1145
1.1851
Про опасности, порождаемые плохой обусловленностью матрицы, написано в разделе Влияние обусловленности матрицы на точность решения системы с ней. Сейчас мы обратимся к обзору имеющихся в MATLAB матричных разложений.