Функция linsolve для решения систем линейных уравнений

Вместо решения системы (или систем с несколькими правыми частями, заданными в матрице) линейных алгебраических уравнений при помощи знака обратной косой черты можно использовать функцию linsolve, которая не делает всех проверок матрицы, заложенных в алгоритме операции \ (см. предыдущий раздел Алгоритм решения системы линейных уравнений при помощи знака обратной косой черты).

Функция linsolve, вызванная в самом простом варианте с двумя входными аргументами и одним выходным аргументом

x = linsolve(A, b)

решает систему Ax = b одним из способов, в зависимости от того, квадратная матрица, или нет.

Если A — квадратная матрица, то предварительно вычисляется ее LU-разложение и затем решаются две системы с треугольными матрицами L и U.

Если A — прямоугольная матрица, то предварительно вычисляется ее QR-разложение и затем решается система с треугольными матрицами.

(Более подробно про действия с полученными множителями разложения написано в разделе Алгоритм решения системы линейных уравнений при помощи знака обратной косой черты). При этом, если матрица A плохообусловлена или A — матрица неполного ранга, то выводится соответствующее предупреждение, например:

A = [1 2 3

2 4 6];

b = [6; 12];

x = linsolve(A,b)

Warning: Rank deficient, rank = 1, tol = 4.4686e-015.

x =

0

0

2.0000

Для подавления вывода данного сообщения в командное окно следует вызывать функцию linsolve с двумя выходными аргументами

[x, r] = linsolve(A, b)

тогда в x запишется полученное решение, а в r — или ранг матрицы (если A является прямоугольной матрицей), или обратная величина к оценке для ее числа обусловленности (см. раздел Влияние обусловленности матрицы на точность решения системы с ней), например

A = [1 2 3

4 5 6

7 8 9+1e-10];

b = [1;1;1] ;

[x, r] = linsolve(A,b)

x =

-1.0000e+000

9.9999e-001

3.3307e-006

r =

6.9444e-013

Основные преимущества функции linsolve над операцией \ проявляются при указании типа матрицы системы уравнений. Для этого перед вызовом функции linsolve надо заполнить структуру с информацией о матрице со следующими полями

SYM — симметричная;

LT — нижняя треугольная;

UT — верхняя треугольная;

UHESS — хессенбергова;

POSDEF — симметричная, положительно определенная;

RECT — прямоугольная;

TRANSA — надо ли решать систему с матрицей, транспонированной к заданной.

Каждое поле может принимать значение либо true, либо false. Разумеется, не все комбинации значений полей допустимы, например матрица не может быть треугольной и в то же самое время симметричной и положительно определенной. Верные комбинации значений полей собраны в следующей

LT UT UHESS SYM POSDEF RECT TRANSA

true false false false false true/false true/false

false true false false false true/false true/false

false false true false false false true/false

false false false true true false true/false

false false false false false true/false true/false

Если матрица системы положительно определена, то это обязательно учесть при решении, поскольку для положительно определенных матриц решение основано на разложении Холецкого, которое требует меньше операций, чем LU-разложение, используемое при решении систем с квадратными матрицами общего вида. В этом несложно убедиться при помощи следующего примера, в котором создается симметричная положительно определенная матрица (матрица из случайных чисел складывается с транспонированной к ней и на диагональ добавляются большие числа) и система уравнений с этой матрицей сначала решается как система с матрицей общего вида (opts.SYM = false и opts.POSDEF = false), а затем — как с симметричной и положительно определенной матрицей (opts.SYM = true и opts.POSDEF = true).

% задаем все поля структуры ops, кроме SYM и POSDEF

opts.TRANSA = false; opts.UHESS = false; opts.RECT = false;

opts.UT = false; opts.LT = false;

% создаем вектор размеров матриц

N = 2.^(8:12);

% создаем пустые массивы для записи времен решения

TimeGeneral = []; TimePosSym = [];

% в цикле создаем матрицы и сравниваем времена решения

for n = N

% создаем симметричную и положительно определенную матрицу

% и вектор правой части

A = rand(n); A = A + A' + 2*n*eye(n); b = sum(A, 2);

% решаем систему как систему с матрицей общего вида

opts.SYM = false; opts.POSDEF = false;

Tstart = cputime;

x = linsolve(A,b, opts);

Tend = cputime; TimeGeneral = [TimeGeneral Tend-Tstart];

% решаем систему как систему с симметр и полож. опред матрицей

opts.SYM = true; opts.POSDEF = true;

Tstart = cputime;

x = linsolve(A,b, opts);

Tend = cputime; TimePosSym = [TimePosSym Tend-Tstart];

end

% выводим графики временных затрат

figure

loglog(N, TimeGeneral, N, TimePosSym)

legend('TimeGeneral', 'TimePosSym')

Получающиеся вычислительные затраты этих способов решения системы приведены на графике ниже

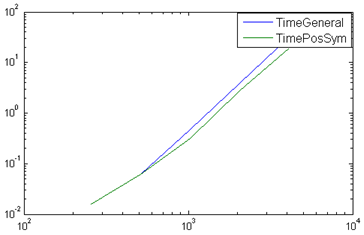
Разумеется, если матрица треугольная, то очень важно это указать, поскольку решение системы с треугольной матрицей выполняется за O(n2) операций, а если к системе с треугольной матрицей применить алгоритм решения, предназначенный для матрицы общего вида, то понадобится порядка O(n3) операций.

Функция linsolve не проверяет, удовлетворяет ли матрица указанным свойствам, что может привести к ошибке. Например, если при решении системы со следующей матрицей и правой частью

A = [1 2 3

2 4 5

3 5 6];

b = [6; 9; 6];

задать true для поля UT (а все остальные установить в false)

opts.UT = true;

opts.TRANSA = false;

opts.LT = false;

opts.UHESS = false;

opts.SYM = false;

opts.POSDEF = false;

opts.RECT = false;

то при решении системы функция linsolve будет рассматривать матрицу как верхнюю треугольную и выберет нужные ей элементы из верхнего треугольника A

x = linsolve(A,b, opts)

При этом получится решение

x =

1

1

1

соответствующее матрице

A = [1 2 3

0 4 5

0 0 6];