
- •5. Визначити екстраполюючу функцію за допомогою регресійного аналізу. Для розрахунків використовуйте систему нормальних рівнянь Гауса. В якості екстрополюючої функції візьміть:
- •6. Провести кореляційний аналіз для оцінки тісноти та значимості зв’язку змінних в регресійній моделі.
- •7.2 Довести, що розподіл випадкової компоненти відповідає нормальному закону.
- •2.8 Визначити довірчий інтервал прогнозу.
Лабораторна робота 2
Складання прогнозу діяльності фірми на основі динамічних рядів
Варіант 6
Мета роботи: ознайомитись з методиками прогнозування, що застосовуються в управлінні фінансами фірми; придбати навички складання прогнозу з використанням електронних таблиць Microsoft Excel.
Теоретичні відомості
Для оцінки майбутніх доходів та інших показників діяльності фірми на основі даних минулих періодів широко використовують екстраполяційні методи. В їх основі лежить припущення, що в силу інерційності економічних процесів тенденція, що складається в минулому, буде незмінна в певних межах. Значення прогнозуючого показника можна представити у вигляді двох компонентів: тренда (тенденції) та випадкової складової (залишків).
Найбільш
простою є методика плинного середнього.
Існує ряд варіантів методу. Найбільш
простий, коли прогнозом на майбутній
період є середня арифметична за кілька
попередніх періодів, число яких називають
інтервалом зглажування із значенням
k.
Іншим підходом, більш складним, є
виділення на динамічному ряді з n
значеннями інтервалів (бажано, щоб
значення інтервалу було непарним) із
зміщенням на один період і розрахунку
середнього арифметичного по кожному
і-тому інтервалу. Таким чином ми отримаємо
точку
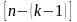 .
При цьому відбувається зглажування
відхилень тим більше, чим більше k.
Отримані при цьому точки є координатами
тренду (тенденції), по якій можна робити
прогноз.
.
При цьому відбувається зглажування
відхилень тим більше, чим більше k.
Отримані при цьому точки є координатами
тренду (тенденції), по якій можна робити
прогноз.
Більш складним та більш точнішим є метод експоненціального зглажування. При цьому методі останнє значення динамічного ряду має більшу вагу. Найбільш поширеним є рекурентний підхід, коли наступне значення визначається на основі попереднього:
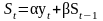 (2.1)
(2.1)
де St – значення експоненціальної середньої у момент t;
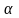 -
параметр зглажування (0<
<1,
-
параметр зглажування (0<
<1,
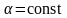 );
);
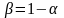 ,
,
або
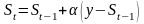 (2.2)
(2.2)
Перше
значення S1
звичайно
приймають S1=y
або
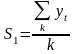
Принципово іншим підходом є описання тренда за допомогою однієї з математичних функцій, вважаючи відхилення динамічного ряду в даних точках випадковими. Найбільше поширення в економіці мають:
Визначенням подібних залежностей займається регресійний аналіз. Найбільш часто при цьому невідомі постійні коефіцієнти ai визначаються з використанням методу найменших квадратів, в основі якого лежить функція Лежандра:
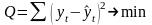 (2.3)
(2.3)
Мінімум функції можна знайти, якщо прирівняти до 0 її першу похідну по невідомим параметрам.
При використанні в якості функції поліному р-тої степені виходить система нормальних рівнянь Гауса:
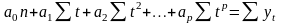
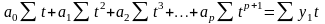
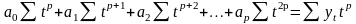
Розв’язавши
цю систему можна визначити невідомі
a0,
a1,
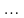 ,
ap.
,
ap.
Після вибору виду функції та знаходження її параметрів необхідно провести кореляційний аналіз для оцінки тісноти та значимості зв’язку в регресійній моделі.
Коефіцієнт детермінації показує, якою мірою варіація залежної змінної визначається варіацією незалежної змінної. Він визначається:
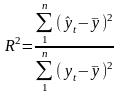 (2.4)
(2.4)
Оцінити значимість зв’язку можна за допомогою критерію Фішера:
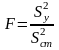 (2.5)
(2.5)
де
 -
факторна дисперсія;
-
факторна дисперсія;
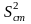 -
дисперсія залишків.
-
дисперсія залишків.
Для коректного використання МНК необхідно довести, що випадкова компонента має наступні властивості:
а) значення залишків є випадковими числами;
б) розподіл випадкової компоненти відповідає нормальному закону;
в) математичне очікування випадкової компоненти дорівнює нулю;
г) рівні випадкової компоненти не повинні авто корелювати.
Для перевірки випадковості значень залишків використовують ряд непараметричних критеріїв, таких як критерій серій і критерій поворотних точок.
Перевірка
відповідності нормальному закону
виконується за допомогою показників
асиметрії
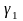 і ексцесу
і ексцесу
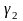 .
.
Для оцінки відповідності нормальному закону використовують також RS- критерій, який чисельно рівний відношенню розмаху варіації випадкової величини R до стандартного відхилення S.
Оцінка математичного очікування випадкової компоненти ведеться з використанням t- критерію Ст’юдента.
Перевірка на відсутність автокореляції виконується на основі d-критерію Дарбіна-Уотсона.
Довірчий інтервал прогнозу для прямолінійного тренду:
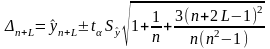 (2.6)
(2.6)
Для поліному 2-го і 3-го порядку:
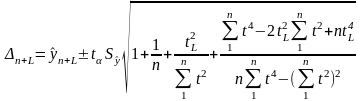 (2.7)
(2.7)
Виконання лабораторної роботи
Використовуючи електронну таблицю Excel ми визначали прогноз у вихідних даних динамічного ряду на чотири періоди вперед.
1. Визначити прогноз на один період вперед використовуючи метод плинного середнього з інтервалом зглажування k=3. Для цього створити таблицю з вихідними даними. Ввести колонку для середніх значень при k=3. Для останніх k значень знайти прогноз на один перід майбутнього. Побудувати графік вихідного динамічного ряду та значення середніх, порівняти та зробити висновки.
2. Використайте для перевірки розрахунків “Пакет аналізу”.
3. Проведіть зглажування методом експоненціального зглажування. Спочатку виконайте зглажування, використовуючи формулу:
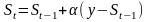
Необхідно виконати розрахунки при =0,4.
Прогноз зробити на один період вперед. Порівняти з плинним середнім і зробити висновки.
Таблиця 2.1 – Вихідні дані
|
Рік |
Видобуток золота у США, т |
t |
Лінійна функція |
Квадратична функція |
|
1960 |
52,8 |
1 |
55,05 |
48,98 |
|
1961 |
48,7 |
2 |
53,84 |
49,69 |
|
1962 |
48,4 |
3 |
52,63 |
50,18 |
|
1963 |
45,7 |
4 |
51,42 |
50,47 |
|
1964 |
45,7 |
5 |
50,21 |
50,53 |
|
1965 |
52,1 |
6 |
49,01 |
50,39 |
|
1966 |
56,1 |
7 |
47,80 |
50,03 |
|
1967 |
47,5 |
8 |
46,59 |
49,46 |
|
1968 |
46,0 |
9 |
45,38 |
48,68 |
|
1969 |
53,9 |
10 |
44,17 |
47,68 |
|
1970 |
54,2 |
11 |
42,97 |
46,48 |
|
1971 |
46,4 |
12 |
41,76 |
45,06 |
|
1972 |
45,1 |
13 |
40,55 |
43,42 |
|
1973 |
36,2 |
14 |
39,34 |
41,58 |
|
1974 |
35,1 |
15 |
38,13 |
39,52 |
|
1975 |
32,4 |
16 |
36,93 |
37,24 |
|
1976 |
32,2 |
17 |
35,72 |
34,76 |
|
1977 |
32,0 |
18 |
34,51 |
32,06 |
|
1978 |
31,1 |
19 |
33,30 |
29,15 |
|
1979 |
29,8 |
20 |
32,09 |
26,03 |
|
1980 |
- |
21 |
30,88 |
22,69 |
|
1981 |
- |
22 |
29,68 |
19,15 |
|
1982 |
- |
23 |
28,47 |
15,39 |
|
1983 |
- |
24 |
27,26 |
11,41 |
|
|
|
|
|
|
Введемо в таблицю вихідні дані, побудуємо колонку для середніх значень при k=3, для цього використаємо функцію СРЗНАЧ. Наприклад, для розрахунку значення плинного середнього для 1962 року знайдемо середній індекс цін за 1960, 1961 та 1962 роки. Для останніх трьох значень знайдемо прогноз на один період майбутнього.
Для здійснення аналізу в меню Сервіс виберемо команду Аналіз даних, в діалоговому вікні якого вибираємо Плинне середнє. Здійснення аналізу показало, що розрахунки в попередньому завданні здійснені вірно.
Виконаємо експоненціальне зглажування, використовуючи формулу 2.2. Наприклад, розрахунок видобутку срібла для 1961 року методом експоненціального зглажування:
0,4*263+0,6*(263-263)=263
Зробимо прогноз на один період вперед. Прогнозне значення видобутку срібла на 1980 рік за даним методом становить 577,35.
Метод експоненціального зглажування є більш складним і більш точним ніж метод плинного середнього. При його використанні останнє значення динамічного ряду має найбільшу вагу.
Для здійснення аналізу в меню Сервіс виберемо команду Аналіз даних, в діалоговому вікні якого вибрати Експоненціальне зглажування. Здійснення аналізу показало, що розрахунки в попередньому завданні здійснені вірно.
Результати розрахунків відображено в таблиці 2.1.
Побудуємо графік вихідного ряду та значення середніх (рисунок 2.1). Ми бачимо, що метод плинного середнього є дуже простим. Він дозволяє здійснити зглажування коливань динамічного ряду. Отримані точки є координатами тренду, за яким можна зробити прогноз. Згідно з нашими даними прогнозний видобуток срібла у США становить 30,88т. Даний метод надто простий для надійного прогнозу.
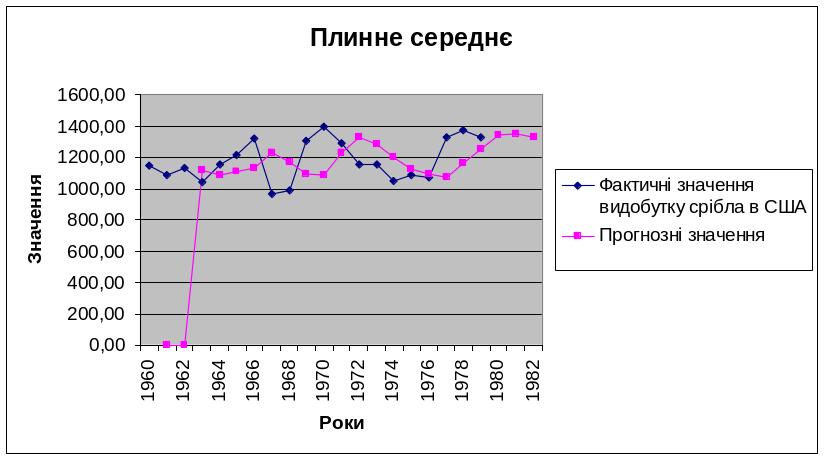
Рисунок 2.1 – Графік вхідного динамічного ряду та значення середніх
5. Визначити екстраполюючу функцію за допомогою регресійного аналізу. Для розрахунків використовуйте систему нормальних рівнянь Гауса. В якості екстрополюючої функції візьміть:
а) лінійну функцію;
б) квадратичну функцію.
Відкриємо у робочій книзі наступний лист і сформуємо в ньому таблицю 2.2.
Таблиця 2.2 – Регресійний аналіз
|
|
|
|
|
|
|
|
|||||
|
Рік |
Видобуток золота у США, т |
t |
Лінійна функція |
Квадратична функція |
|||||||
|
1960 |
52,8 |
1 |
55,05 |
48,98 |
|||||||
|
1961 |
48,7 |
2 |
53,84 |
49,69 |
|||||||
|
1962 |
48,4 |
3 |
52,63 |
50,18 |
|||||||
|
1963 |
45,7 |
4 |
51,42 |
50,47 |
|||||||
|
1964 |
45,7 |
5 |
50,21 |
50,53 |
|||||||
|
1965 |
52,1 |
6 |
49,01 |
50,39 |
|||||||
|
1966 |
56,1 |
7 |
47,80 |
50,03 |
|||||||
|
1967 |
47,5 |
8 |
46,59 |
49,46 |
|||||||
|
1968 |
46,0 |
9 |
45,38 |
48,68 |
|||||||
|
1969 |
53,9 |
10 |
44,17 |
47,68 |
|||||||
|
1970 |
54,2 |
11 |
42,97 |
46,48 |
|||||||
|
1971 |
46,4 |
12 |
41,76 |
45,06 |
|||||||
|
1972 |
45,1 |
13 |
40,55 |
43,42 |
|||||||
|
1973 |
36,2 |
14 |
39,34 |
41,58 |
|||||||
|
1974 |
35,1 |
15 |
38,13 |
39,52 |
|||||||
|
1975 |
32,4 |
16 |
36,93 |
37,24 |
|||||||
|
1976 |
32,2 |
17 |
35,72 |
34,76 |
|||||||
|
1977 |
32,0 |
18 |
34,51 |
32,06 |
|||||||
|
1978 |
31,1 |
19 |
33,30 |
29,15 |
|||||||
|
1979 |
29,8 |
20 |
32,09 |
26,03 |
|||||||
|
|
|
|
|
|
|||||||
На основі таблиці 2.2 заповнимо таблиці коефіцієнтів нормальних рівнянь Гауса. Знайдемо визначники для знаходження параметрів лінійної функції (таблиця 2.3).
Таблиця 2.3 – Визначники для знаходження параметрів лінійної та квадратичної функцій
|
Лінійна функція |
Квадратична функція |
|||||
|
Детермінант (Δ) |
||||||
|
20 |
210 |
13300 |
20 |
210 |
2870 |
233494800 |
|
210 |
2870 |
210 |
2870 |
44100 |
||
|
|
|
|
2870 |
44100 |
722666 |
|
|
Визначник (Δ0) |
||||||
|
871,4 |
210 |
748195 |
871,4 |
210 |
2870 |
11222907080 |
|
8346,3 |
2870 |
8346,3 |
2870 |
44100 |
||
|
|
|
|
106307,1 |
44100 |
722666 |
|
|
Визначник (Δ1) |
||||||
|
20 |
871,4 |
-16068 |
20 |
871,4 |
2870 |
239475012 |
|
210 |
8346,3 |
210 |
8346,3 |
44100 |
||
|
|
|
|
2870 |
106307,1 |
722666 |
|
|
Визначник (Δ2) |
||||||
|
|
20 |
210 |
871,4 |
-24836420 |
||
|
210 |
2870 |
8346,3 |
||||
|
2870 |
44100 |
106307,1 |
||||
|
Коефіцієнт а0 |
||||||
|
56,2553 |
48,0649 |
|||||
|
Коефіцієнт а1 |
||||||
|
-1,2081 |
1,0256 |
|||||
|
Коефіцієнт а2 |
||||||
|
|
-0,1064 |
|||||
|
Рівняння |
||||||
|
у=56,2553-1,2081х |
у=48,0649+1,0256х-0,1064х2 |
|||||
Значення регресійних функцій записані в таблиці 2.4
Таблиця 2.4– Регресійні функції
|
Рік |
Видобуток золота у США, т |
t |
Лінійна функція |
Квадратична функція |
|
1960 |
52,8 |
1 |
55,05 |
48,98 |
|
1961 |
48,7 |
2 |
53,84 |
49,69 |
|
1962 |
48,4 |
3 |
52,63 |
50,18 |
|
1963 |
45,7 |
4 |
51,42 |
50,47 |
|
1964 |
45,7 |
5 |
50,21 |
50,53 |
|
1965 |
52,1 |
6 |
49,01 |
50,39 |
|
1966 |
56,1 |
7 |
47,80 |
50,03 |
|
1967 |
47,5 |
8 |
46,59 |
49,46 |
|
1968 |
46,0 |
9 |
45,38 |
48,68 |
|
1969 |
53,9 |
10 |
44,17 |
47,68 |
|
1970 |
54,2 |
11 |
42,97 |
46,48 |
|
1971 |
46,4 |
12 |
41,76 |
45,06 |
|
1972 |
45,1 |
13 |
40,55 |
43,42 |
|
1973 |
36,2 |
14 |
39,34 |
41,58 |
|
1974 |
35,1 |
15 |
38,13 |
39,52 |
|
1975 |
32,4 |
16 |
36,93 |
37,24 |
|
1976 |
32,2 |
17 |
35,72 |
34,76 |
|
1977 |
32,0 |
18 |
34,51 |
32,06 |
|
1978 |
31,1 |
19 |
33,30 |
29,15 |
|
1979 |
29,8 |
20 |
32,09 |
26,03 |
|
1980 |
- |
21 |
30,88 |
22,69 |
|
1981 |
- |
22 |
29,68 |
19,15 |
|
1982 |
- |
23 |
28,47 |
15,39 |
|
1983 |
- |
24 |
27,26 |
11,41 |
Функція ЛИНЕЙН повертає значення параметра а1 лінійної функції. Результати перевірки за допомогою команди Регресія занесено в таблицю 2.5
