
- •Линейная алгебра Основные определения
- •Операция умножения матриц
- •Свойства операции умножения матриц
- •Определители (детерминанты)
- •Алгебраические дополнения
- •Обратная матрица
- •Базисный минор матрицы Ранг матрицы
- •Матричный метод решения систем линейных уравнений
- •Метод Крамера
- •Элементарные преобразования систем
- •Теорема Кронекера – Капелли
- •Метод Гаусса
- •Элементы векторной алгебры
- •Свойства векторов
- •Линейная зависимость векторов
- •Система координат
- •Декартова система координат
- •Линейные операции над векторами в координатах Пусть заданы векторы в прямоугольной системе координат
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Свойства смешанного произведения:
- •Уравнение поверхности в пространстве
- •Общее уравнение плоскости
- •Пусть заданы точки м1(x1, y1, z1), m2(x2, y2, z2) и вектор .
- •Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки м(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.
- •Полярная система координат
- •Линейное (векторное) пространство
- •Линейные преобразования
- •Матрицы линейных преобразований
- •Собственные значения и собственные векторы линейного преобразования
- •Введение в математический анализ Предел функции в точке
- •Предел функции при стремлении аргумента к бесконечности
- •Основные теоремы о пределах
- •Некоторые замечательные пределы
- •Комплексные числа
- •Тригонометрическая форма числа
- •Действия с комплексными числами
- •Дифференциальное исчисление функции одной переменной Производная функции, ее геометрический и физический смысл
- •Основные правила дифференцирования
- •Производные основных элементарных функций
- •Производная сложной функции
- •Логарифмическое дифференцирование
- •Производная показательно- степенной функции
- •Производная обратных функций
- •Точки экстремума
- •Асимптоты
- •Вертикальные асимптоты
- •Наклонные асимптоты
- •Векторная функция скалярного аргумента
- •Параметрическое задание функции
- •Производная функции, заданной параметрически
- •Функции нескольких переменных
- •Производные и дифференциалы функций нескольких переменных
- •Полное приращение и полный дифференциал
- •Геометрический смысл полного дифференциала Касательная плоскость и нормаль к поверхности
- •Приближенные вычисления с помощью полного дифференциала
- •Частные производные высших порядков
- •Экстремум функции нескольких переменных
- •Условный экстремум
- •Производная по направлению
- •Градиент
- •Связь градиента с производной по направлению
Линейные операции над векторами в координатах Пусть заданы векторы в прямоугольной системе координат
![]() тогда
линейные операции над ними в координатах
имеют вид:
тогда
линейные операции над ними в координатах
имеют вид:
![]()
Скалярное произведение векторов
Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.
= cos
Свойства скалярного произведения:
= 2;
= 0, если или = 0 или = 0.
= ;
( +
 )
=
+
;
)
=
+
;(m ) = (m ) = m( ); m=const
Если
рассматривать векторы
![]() в
декартовой прямоугольной системе
координат, то
в
декартовой прямоугольной системе
координат, то
= xa xb + ya yb + za zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
![]() .
.
Пример.
Найти (5
+ 3
)(2
-
),
если
![]()
10
-
5
+
6
-
3
= 10![]() ,
,
т.к.
![]() .
.
Пример.
Найти угол между векторами
и
,
если
![]()
![]() .
.
Т.е. = (1, 2, 3), = (6, 4, -2)
= 6 + 8 – 6 = 8:
![]() .
.
cos
=
![]()
Пример.
Найти скалярное произведение (3
- 2
)(5
- 6
),
если
![]()
15
-
18
-
10
+
12
= 15![]()
+ 1236 = 240 – 336 + 432 = 672 – 336 = 336.
Пример.
Найти угол между векторами
и
,
если
![]()
![]() .
.
Т.е. = (3, 4, 5), = (4, 5, -3)
= 12 + 20 - 15 =17 :
![]() .
.
cos
=
![]()
Пример.
При каком m
векторы
![]() и
и
![]() перпендикулярны.
перпендикулярны.
= (m, 1, 0); = (3, -3, -4)
![]() .
.
Пример.
Найти скалярное произведение векторов
![]() и
и
![]() ,
если
,
если
![]()
(
)(
)
=
![]()
![]()
![]() =
10 +
=
10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
Векторное произведение векторов
Определение. Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:
1)
![]() ,
где
- угол между векторами
и
,
,
где
- угол между векторами
и
,
![]()
2) вектор ортогонален векторам и
3) , и образуют правую тройку векторов.
Обозначается:
![]() или
или![]() .
.

Свойства векторного произведения векторов:
1)
![]() ;
;
2)
![]() ,
если
или
=
0 или
=
0;
,
если
или
=
0 или
=
0;
3) (m ) = (m ) = m( );
4) ( + ) = + ;
5)
Если заданы векторы
(xa,
ya,
za)
и
(xb,
yb,
zb)
в декартовой прямоугольной системе
координат с единичными векторами
![]() ,
то
,
то
=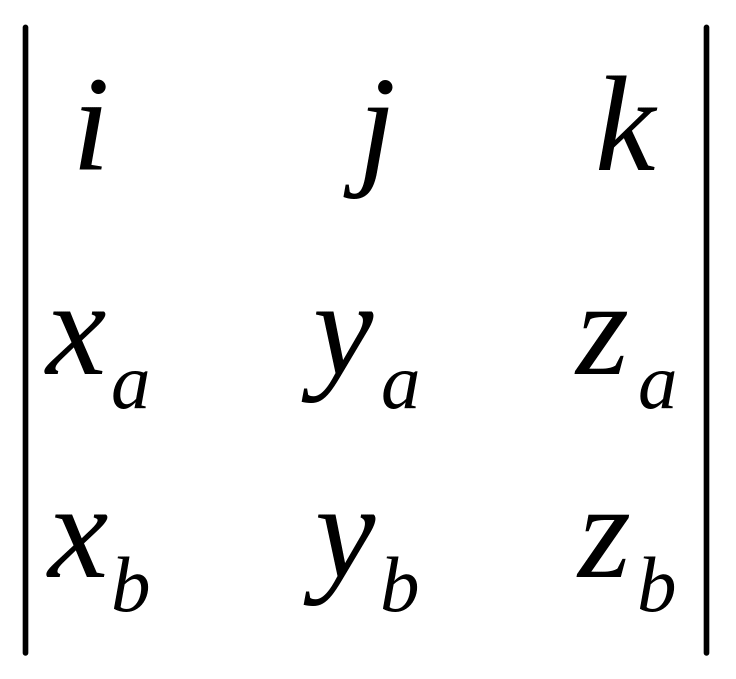
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .
Пример.
Найти векторное произведение векторов
![]() и
и
![]() .
.
= (2, 5, 1); = (1, 2, -3)
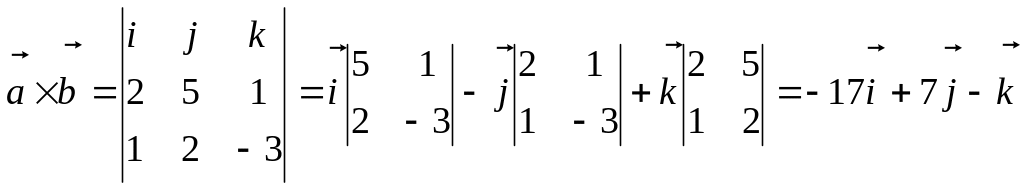 .
.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),С(0, 1, 0).
![]()

![]()
![]() (ед2).
(ед2).
Пример.
Доказать, что векторы
![]() ,
,
![]() и
и
![]() компланарны.
компланарны.
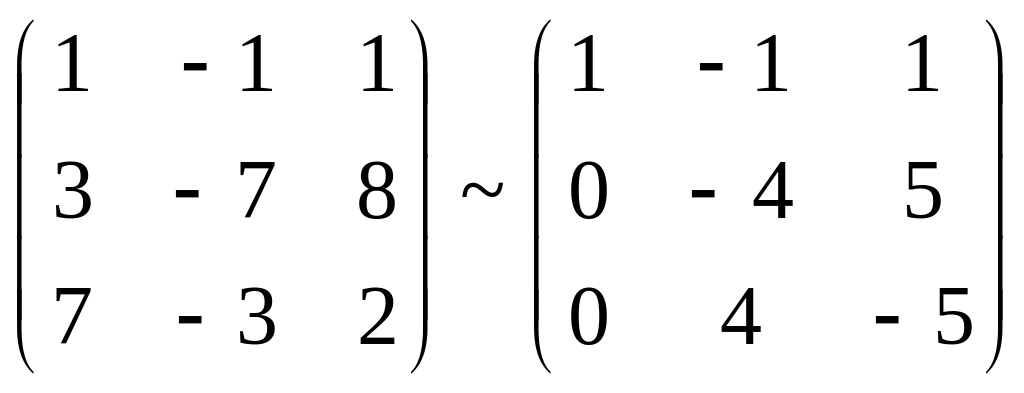 ,
т.к. векторы линейно зависимы, то они
компланарны.
,
т.к. векторы линейно зависимы, то они
компланарны.
Пример.
Найти площадь параллелограмма,
построенного на векторах
![]() ,
если
,
если
![]()
![]()
![]() (ед2).
(ед2).
Смешанное произведение векторов
Определение. Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и .
Обозначается
![]() или
(
,
,
).
или
(
,
,
).
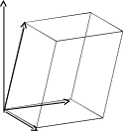
Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .
![]()
