Нониусы

Нониусом называется специальная шкала, дополняющая масштаб обычной шкалы и позволяющая повысить точность измерений в 10-20 раз.

Нониусы бывают линейные (например, штангенциркуль) и круговые (например, микрометр). Ниже рассмотрим принцип построения линейного нониуса, который представляет собой небольшую линейку, скользящую вдоль основной шкалы. Интервал b одного деления нониуса меньше k интервалов деления a основной шкалы на величину δ=k·a−b. Если принять δ=, где N - целое, то длина N делений нониуса равна длине N·k-1 делений основной шкалы, т.е. N·b=(N·k-1)·a. 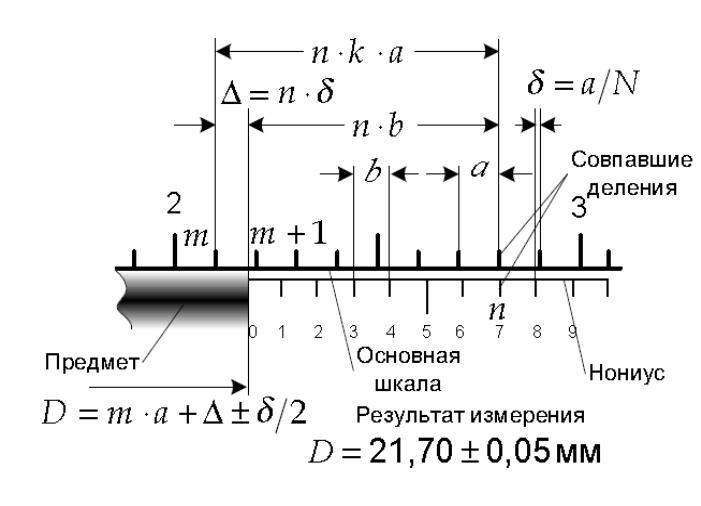Пусть длина D измеряемого предмета такая, что m·a<D<(m+1)·a. (см. рисунок). Если n-ое деление нониуса совпадает с некоторым делением основной шкалы, то длина предмета . Следовательно, минимальное отличие длины предмета от целого числа делений основной шкалы, которое можно измерить по нониусу, равно δ и составляет N-ю долю цены деления основной шкалы. Значение δ указывается как цена деления на измерительном приборе.

Литература

1. Брянский Л.Н., Дойников А.С. Краткий справочник метролога. - М.: Издательство стандартов, 1991.

2. Кушнир Ф.В., Савенко В.Г. Электрорадиоизмерения. - Л.: Энергия, 1975.

3. Тейлор Дж. Введение в теорию ошибок. - М.: Мир, 1985.

4. Сквайрс Дж. Практическая физика. - М.: Мир, 1971.

5. Худсон Д. Статистика для физиков. - М.: Мир, 1970.

6. Кунце Х.-И. Методы физических измерений. - М.: Мир, 1989.

7. Тойберт П. Оценка точности результатов измерений. - М.: Энергоатомиздат, 1988.

8. Каленко С.Г., Соломахо Г.И. Практикум по физике. Механика. - М.:Высш. шк., 1990

9. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. - М.: Высш. шк., 1965.