ЛАБОРАТОРНАЯ РАБОТА 1-2

ЛАБОРАТОРНАЯ РАБОТА 1-2

ИССЛЕДОВАНИЕ СЛОЖЕНИЯ ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ С ПОМОЩЬЮ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА

1. ЦЕЛЬ РАБОТЫ: ознакомление с работой электронного осциллографа, градуировка звукового генератора.

2. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: осциллограф, звуковой генератор.

3. МЕТОД ИЗМЕРЕНИЙ: с помощью осциллографа изучается сложение двух взаимно-перпендикулярных колебаний электронного луча.

4. ВВЕДЕНИЕ.

СЛОЖЕНИЕ ДВУХ ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ.

Рассмотрим сложение двух взаимно-перпендикулярных колебаний на примере колебаний луча электронного осциллографа (ЭО). Электронный луч в электронно-лучевой трубке (рис.1) перед попаданием на экран проходит между двумя парами управляющих пластин 1-2 и 3-4. Если на пластины 1-2 подать переменное напряжение, то, совершая колебания, след электронного луча прочерчивает на экране вертикальную линию по оси Y. При том же напряжении, поданном на пластины 3-4, электронный луч прочерчивает линию по оси X. Если переменное напряжение одинаковой частоты  подать на пластины 1-2 и на пластины 3-4, то электронный луч будет одновременно участвовать в двух взаимно-перпендикулярных колебаниях:

(1.2.1.)

(1.2.2.)

Рис. 1

где A и B – амплитуда колебаний;  - разность фаз колебаний;  - циклическая частота, связанная с частотой  соотношением:

 = 2

Найдем уравнение траектории результирующего колебания. Запишем уравнения складываемых колебаний в виде:

(1.2.3.)

(1.2.4.)

В уравнении (1.2.4.) выразим cos t через , а

sin t = через , тогда получим :

sin (1.2.5.)

После возведения в квадрат обеих частей уравнения (1.2.5.) и несложных преобразований получаем:

(1.2.6.)

Это уравнение эллипса, вписанного в прямоугольник со сторонами 2A и 2B, ориентировка осей которого зависит от разности фаз .

Рассмотрим некоторые частные случаи (см. рис.2):

1. При  = 0 (рис.2a), эллипс вырождается в прямую, уравнение которой

(1.2.7.)

2. При (рис.2б), след электронного луча движется по часовой стрелке по эллипсу, уравнение которого имеет вид:

(1.2.8.)

3. При эллипс будет таким же, как и на рис.2б, только вращение луча будет происходить против часовой стрелки.

4. При  =  (рис.2в) колебания луча происходят по прямой, уравнение которой

Y = - (1.2.9.)

5. При  = 2 траектория будет такой же, как и при  = 0.

Уравнения (1.2.7.), (1.2.8.) и (1.2.9.) получите сами, используя уравнение (1.2.6.).

Рис. 2

Рассмотрим сложение двух взаимно-перпендикулярных колебаний с различными частотами _x и _y, уравнения которых имеют вид:

X = A cos 2_xt (1.2.10.)

Y = B cos 2_y t (1.2.11.)

где _x – частота колебаний вдоль оси X;

_y – частота колебаний вдоль оси Y.

Пусть _x немного больше _y. Разность фаз этих колебаний 2(_x - _y)t с течением времени растет, последовательно проходя значения 0, /2, , 3/2, 2 и т.д. При этом эллипс на экране последовательно принимает формы, изображенные на рисунке 2а, 2б, 2в и т.д. Конфигурация эллипса повторяется через промежуток времени T (период колебания), за который разность фаз увеличивается на 2.

Отсюда следует: 2(_x - _y)T = 2. После сокращения на 2 получаем:

_x - _y=1/T= (1.2.12)

где  - частота повторения конфигурации.

Если отношение частот складываемых колебаний _x : _y равно отношению целых чисел, то материальная точка движется по сложным замкнутым кривым, называемым фигурами Лиссажу. На рис. 3 представлены фигуры Лиссажу для соотношения частот 1:2, 1:3, 2:3, 3:4 (и обратных отношений) и различных разностей фаз:  = 0, /4, /2, 3/4, .

νx: νy=1:1

νx: νy=2:1

νx: νy=3:1

νx: νy=3:2

νx: νy=4:3

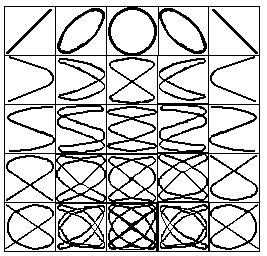
Рис. 3

Рассмотрим одну из фигур, изображенных на рис.3, и мысленно проведем любую прямую параллельно оси X. Она пересечет фигуру Лиссажу n_x раз, а любая прямая параллельная оси Y пересечет ее n_y раз. Оказывается, что частоты колебаний _x и _y связаны с числом пересечения n_x и n_y простым соотношением:

(1.2.13.)

Это легче проверить, пользуясь рисунком 3, на котором слева указаны отношения частот _x/_y, а в верхней строке - значения разности фаз  складываемых колебаний.

5. КРАТКОЕ ОПИСАНИЕ ПРИМЕНЯЕМЫХ ПРИБОРОВ.

5.1. ЭЛЕКТРОННЫЙ ОСЦИЛЛОГРАФ (ЭО)

На рис.4 изображена передняя панель осциллографа С1-1, на которой расположены экран электронно-лучевой трубки и основные ручки управления. С помощью тумблера «Сеть» включается блок питания осциллографа. Электронный луч фокусируется ручкой «Фокус», а его интенсивность задается ручкой «Яркость». Ручки «Ось X» и «Ось Y» смещают луч в соответствующих направлениях.

Исследуемый сигнал, подаваемый на «Y-вход», подводится к левым клеммам «Вход» и «Земля». Амплитуда сигнала регулируется ручками «Усилие» (плавная регулировка) и «Ослабление» (грубая регулировка). Сигнал, подаваемый на «X-вход», подводится к правым клеммам «Вход» и «Земля». Амплитуда регулируется ручкой «Усиление X» (плавная регулировка).

Осциллограф может работать в двух режимах. В первом режиме исследуемое напряжение (внешний сигнал) подается на «Y-вход» (рис. 4), а на «X-вход» подается пилообразное напряжение (рис. 5), вырабатываемое специальным генератором, находящимся внутри осциллографа. Это напряжение периодически вызывает равномерное движение светящегося пятна на экране в горизонтальном направлении.

При подаче переменного напряжения на «Y-вход» и пилообразного напряжения на «X-вход» пятно на экране осциллографа вычерчивает кривую, изображающую зависимость исследуемого напряжения от времени. Если, например, период синусоидального напряжения T, подаваемого на «Y-вход» равен периоду пилообразного напряжения Т₀, то на экране получается отрезок синусоиды за один период. Если T₀ в два раза больше T, на экране будет виден отрезок синусоиды за два периода и т.д.

При работе в первом режиме ручку «Диапазон частот» ставят в одно из положений «2», «7», «30», …

Во втором режиме на «X-вход» и «Y-вход» подаются два различных внешних сигнала. При работе в этом режиме ручку «Диапазоны частот» ставят в положение «выключено». В данной работе в этом режиме исследуется сложение взаимно перпендикулярных колебаний.

Рис. 4

Рис. 5

5.2. ЗВУКОВОЙ ГЕНЕРАТОР (ГЗ).

Обычно звуковые генераторы применяются для получения синусоидального напряжения с частотой 20-20000 Гц. На рис. 6 изображена лицевая панель звукового генератора, применяемого в данной работе. Грубое изменение частоты производится переключателем диапазонов (рис. 6). Плавная регулировка частоты производится поворотом диска со шкалой. Когда рукоятка переключателя диапазонов находится в положении «х1», на выходные клеммы генератора подается напряжение с частотой от 20 до 200 Гц. Как раз в таком положении должен находиться переключатель диапазонов при проведении данной работы. Напряжение снимается с пары клемм «Земля-5 Ом» или «Земля-600 Ом».

На диске генератора находится шкала, в середине которой нанесена жирная черная метка. Когда эта метка располагается против указателя шкалы (рис. 6), на выходные клеммы генератора подается напряжение с частотой

50 Гц.

Рис. 6

6. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

6.1. Изучение режимов работы ЭО.

6.1.1. Перед включением ЭО установите ручки регуляторов: «Яркость» в крайнее правое положение, «Фокус» - среднее, «Усиление» - нулевое положение, «Усиление Х» - среднее положение, «Диапазоны частот» - в положение «2», «7» или «30». Вилку шнура питания включите в сеть и установите тумблер «Сеть» в верхнее положение, на панели должна загореться контрольная лампочка, а на экране должна появиться светящаяся линия, параллельная оси Х. Затем поворотом ручек «Яркость» и «Фокус» уменьшают яркость и фокусируют луч.

6.1.2. Поставьте рукоятку «Диапазон частот» в положение «2», рукоятку «Частота» плавно поверните против часовой стрелки до упора и наблюдайте периодическое движение светящегося пятна вдоль оси Х.

6.1.3. Рукоятку «Синхронизация» установите в положение «от сети». Соедините проводником клемму «Контрольный сигнал» (частота сигнала

50 Гц) с клеммой «Y-вход», переключатель «Ослабление» в положение «1:1», переключатель «Диапазон частот» в положение «7». Вращением ручек «частота плавно» и «Амплитуда синхронизации» получите устойчивую осциллограмму. Регуляторами «Усиление Х» и «Усиление Y» установите желаемые размеры осциллограммы.

6.1.4. Изменяя частоту развертки поворотом рукояток «Частота плавно», получите на экране отрезки синусоиды, соответствующие 5, 4, 3, 2, 1 периодам колебаний. Зарисуйте одну из полученных осциллограмм.

6.2. Изучение взаимно перпендикулярных колебаний.

6.2.1. Клемму «общ» ГЗ соедините с клеммой «Земля» ЭО, а клемму «5 Ом» ГЗ соедините с клеммой «X-вход» ЭО. Рукоятку «Диапазон частоты» ЭО поставьте в положение «Выключено». Рукоятку «Синхронизация» поставьте в положение «Внеш». «Диапазоны частот» ГЗ поставьте в положение «х1». Поворотом диска ГЗ метку шкалы «50 Гц» установите против указателя шкалы. Включите в сеть ГЗ. Вращением ручек «Регулятор напряжения» ГЗ, «Усиление Х» ЭО получите светящийся след электронного луча длиной 4-6 см. Наблюдайте возникающий на экране эллипс, конфигурация которого постепенно изменяется. Очень медленно поворачивая диск ГЗ, добейтесь устойчивого положения эллипса на экране. Зарисуйте его. В этом случае эллипс возникает в результате сложения взаимно перпендикулярных колебаний луча с одинаковыми частотами колебаний

_x = _y = 50 Гц.

6.2.2. Плавно изменяя частоту _x поворотом диска ГЗ, получайте устойчивые фигуры Лиссажу, соответствующие соотношению частот _x/_y= 1:3, 1:2, 2:3, 1:1, 4:3, 3:2, 2:1, 3:1 (см. формулу (1.2.13) и рис.3).

6.2.3. Для каждого из указанных отношений _x/_y замечают угол поворота диска в делениях шкалы m. Значения m и _x заносят в таблицу 1.

Таблица 1

x/y	1:3	1:2	2:3	1:1	4:3	3:2	2:1	3:1
m
x

6.2.4. По формуле подсчитывают частоту _x переменного напряжения, подаваемого от ГЗ на «X-вход» осциллографа.

6.2.5. По данным таблицы строят график градуировки шкалы звукового генератора. При построении графика по оси абсцисс откладывают деления шкалы m (в угловых градусах), по оси ординат частоту _x (Гц).

7. КОНТРОЛЬНЫЕ ВОПРОСЫ.

7.1. Поясните устройство электронно-лучевой трубки и принцип ее работы.

7.2. Объясните метод получения развертки исследуемого сигнала в осциллографе.

7.3. Как по виду фигуры Лиссажу можно определить отношение частот складываемых колебаний?

8. ЛИТЕРАТУРА.

8.1. Трофимова Т.И., Курс физики, М.: 1990, 478 с., §§ 144, 145.

8.2. Савельев И.В., Курс общей физики, Т.1, Механика и молекулярная физика, М.: Наука. 1982, 432 с., § 57.

8.3. Савельев И.В., Курс общей физики, Т.2, Электричество и магнетизм. Волны. Оптика. М.: Наука. 1982, 496 с., § 73.