
Лекции по физике
.pdf
КИНЕМАТИКА
1.Системы координат.
1.Декартова система координат. Все ниже рассматриваемые системы являются ортогональными (все оси координат взаимно перпендикулярны). Все системы приведены для трехмерного пространства. В декартовой системе оси обозначаются X, Y, Z и нумеруются 1, 2, 3 соответственно (так называемая правовинтовая система). Бесконечно малое перемещение по осям dx , dy , dz . Бесконечно малое расстояние между двумя
точками и бесконечно малое перемещение соответственно равны:
|
|
|
ds = dx2 + dy2 + dz2 |
dr = exdx + ey dy + ez dz |
|
Скалярные произведения ортов равны: |
|
|
exex =1 eyey =1 ezez =1
остальные произведения равны нулю. Векторные произведения ортов равны:
[exey ] = ez [eyez ] = ex [ezex ] = ey
остальные произведения равны нулю. Напомню, что при изменении порядка сомножителей, меняется знак произведения. Поэтому, чтобы избежать в дальнейшем ошибок (особенно в третьем семестре), следует всегда пользоваться правовинтовой системой. Именно для нее написаны три последних равенства.
2. Цилиндрическая система координат. Вертикальная ось Z совпадает по направлению с аналогичной осью декартовой системы. Вторую координату-расстояние точки от оси Z всегда будем обозначать R. В отличие от постоянного орта ez , направление остальных
двух ортов переменное. Орт eR направлен от вертикальной оси по направлению радиуса R. Третья координата угол поворота этого радиуса φ (орт eϕ ), если смотреть сверху, против часовой стрелке (от оси X). Перемещения по осям: eRdR , eϕ Rdϕ , ez dz , перемещение
бесконечно малое между двумя точками
dr = eRdR + eϕ Rdϕ + ez dz
Расстояние между ними
ds = 
 dR2 + R2dϕ2 + dz2
dR2 + R2dϕ2 + dz2
Для скалярного произведения правила аналогичные. Произведение одинаковых ортов всегда равно единице, разных-нулю. Векторные произведения ортов:
[eReϕ ] = ez |
[eϕ ez ] = eR |
[ezeR ] = eϕ |
Связь декартовых координат с цилиндрическими: |
|
|
x = R cosϕ y |
y = R sinϕ |
z = z |
Обратные преобразования практически нам будут не нужны.
3. Сферическая система координат. Вертикальная ось Z совпадает по направлению с аналогичной осью декартовой системы. Первая координата расстояние точки от начала координат принято во всем мире обозначать r . Теперь представьте себе глобус (или, кто его не видел, арбуз). Вторая координата задается углом θ, который отсчитывается от положительного направления оси Z по меридиану (или по направлению движения ножа, когда режете арбуз). Третья координата такая же, как и в цилиндрической системе координат. Орт er направлен от начала координат по направлению радиуса r. Второй орт
eθ направлен по касательно к дуге в сторон направления угла θ. Третий орт eϕ направлен
по углу φ (совпадает с цилиндрической системой). Остальные формулы выпишу без пояснений, так как смысл ясен из выше написанного.
dr = er dr + eθ rdθ + eϕ r sinθdϕ
ds = |
dr2 + r2dϕ2 + r2 sin2 θdϕ2 |
|
|
[er eθ ] = eϕ |
[eθ eϕ ] = er |
[eϕer ] = eθ |
|
x = r sinθ cosϕ |
y = R sinθ sinϕ |
z = r cosθ |
|
PDF created with pdfFactory Pro trial version www.pdffactory.com

2. Скорость и ускорение в цилиндрической системе координат.
Дифференцирование вектора по времени. В общем случае вектор (являющийся функцией времени) за малое время dt может, как изменить свою длину, так и изменить ориентацию в пространстве. С точки зрения математики, далее приведенные рисунки некорректны, так как нарисовать бесконечно малый вектор нельзя. Надо было бы сначала везде писать не dt , а t , и только в окончательных формулах от
малых конечных разностей переходить к пределу бесконечно малых. Физики не придерживаются такой скрупулезности. На
первом рисунке из одной точки проведены два вектора некоторой физической величины в момент времени t и в момент времени t + dt . Может возникнуть вопрос: почему два вектора в разное время можно рисовать из одной точки?. Если
это вектор скорости, то он приложен к телу (или, проще, к материальной точке), а оно за время dt переместилось? Ответ простой. Мы хотим найти изменение вектора по времени, а не как он изменился относительно системы координат в пространстве. Из рисунка видно, вектор dA можно представить как сумму двух векторов параллельного и перпендикулярного перемещение конца вектора A . Первый равен отрезку, на которой изменился модуль вектора (в данном случае величина вектор увеличилась), в пределе он будет направлен по орту eA ,
величина второго в педеле будет равна Adϕ . И его направление перпендикулярно вектору A . Если ввести вектор бесконечно малого поворота dϕ , направленного перпендикулярно
плоскости рисунка на нас, то второй вектор можно записать в виде векторного произведения [dϕ, A] . Чтобы получить производную по времени вектора A , надо оба слагаемых поделить
dt :
A& = ddtA = eAA& +[ddtϕ , A]+ = eAA& +[ω, A]
Еще раз подобное будет показано при дифференцировании переменных ортов цилиндрической системы координат. Тогда все поймете окончательно.
Правило дифференцирования ортов. На рисунке в плоскости
перпендикулярной оси Z показаны орт eR в начальный момент
времени и положение этого орта через бесконечно малый интервал времени dt . Он обозначен как eR/ . Как видно из рисунка за время dt орт eR повернется на угол dφ. Приращение этого
орта будет равно
deR = eR/ - eR = eϕ ×1×dϕ
А производная eR по времени будет равна:
e&R = ddteR = eϕ ddtϕ = eϕϕ/&
Совершенно аналогично выводится производная по времени от орта eϕ . Она будет равна:
e&ϕ = ddteϕ = -eR ddtϕ = -eRϕ/&
На втором рисунке вектор R с разрывом, чтобы уменьшить размер рисунка.
Скорость. Теперь можно приступить непосредственно к вычислению скорости. Используя выше приведенную формулу, получим:
v = dR = |
d(eR R) |
= |
deR |
R + e |
R |
dR = e |
R |
R& + e Rϕ& |
|
|
|||||||
dt |
dt |
|
dt |
dt |
ϕ / |
|||
|
|
|
|
|||||
PDF created with pdfFactory Pro trial version www.pdffactory.com
Модуль скорости будет равна:
v = 
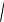 R&2 + R2ϕ/&2
R&2 + R2ϕ/&2
Ускорение. Чтобы найти ускорение надо полученное выражение еще раз
продифференцировать по времени: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dv d(e |
|
|
& |
|
|
d(e Rϕ&) |
|
de |
|
|
|
& |
|
|
de |
|
|
|
|
dR |
|
dϕ& |
||||||||
|
R |
R) |
|
|
|
ϕ |
|
/ |
|
R |
& |
dR |
|
|
|
ϕ |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
||||||
a = |
|
= |
|
|
|
|
|
+ |
|
|
|
|
|
= |
|
|
|
|
R + e |
R dt |
+ |
|
|
Rϕ& |
+ e ϕ& |
|
+ e R |
|
|||
dt |
dt |
|
|
|
|
|
dt |
|
|
|
dt |
|
dt |
|
dt |
||||||||||||||||
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
|
|
|
/ |
ϕ / dt |
ϕ |
||||||||||||
|
|
|
& |
|
|
|
− e |
|
Rϕ& |
2 |
+ e |
|
& |
|
+ e Rϕ&& = e |
|
|
&& |
− Rϕ& |
2 |
|
|
|
& |
|||||||
a = e ϕ&R + e |
R |
R |
R |
|
ϕ&R |
R |
(R |
|
) + e (Rϕ&&+ 2ϕ&R) |
||||||||||||||||||||||
|
|
ϕ / |
|
|
|
|
|
|
/ |
|
|
ϕ |
/ |
|
|
|
ϕ |
|
|
|
|
/ |
|
|
ϕ |
|
/ |
|
|||
До сих пор рассматривалось плоское движение (в плоскости перпендикулярной оси Z). Если движение происходит в трех измерениях, то к полученным формулам надо добавить скорость и ускорение по оси Z.
Выпишем для удобства использования окончательные формулы:
|
|
v = e |
R |
R& + e Rϕ& + e |
z& |
(1) |
|||||
|
|
&& |
|
|
ϕ |
/ |
z |
|
& |
|
|
a = e |
|
− Rϕ& |
2 |
|
|
|
|
&&z (2) |
|||
R |
(R |
|
) + e (Rϕ&&+ 2ϕ&R) + e |
||||||||
|
|
/ |
|
ϕ |
|
|
/ |
z |
|
||
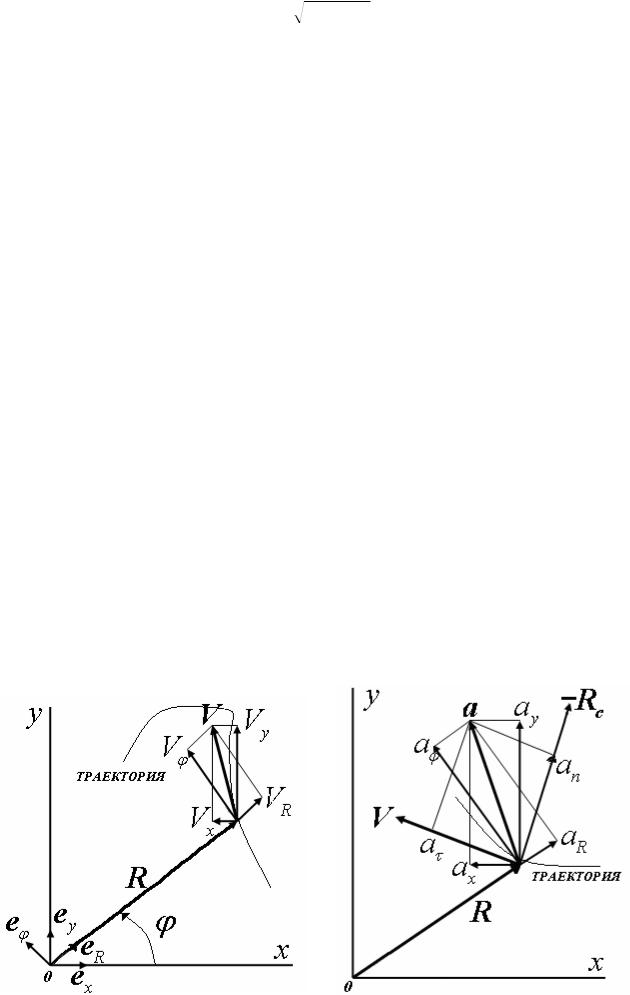
На ниже приведенных рисунках показаны разложение векторов скорости и ускорения. Под ними дано краткое пояснение.
Рассматривается плоское (в данном случае в плоскости X, Y) движение частицы (материальной точки). На первом рисунке показаны все орты по соответствующим осям в декартовой и полярной системах координат, на вторам они такие же, но опущены для экономии времени на изготовления рисунка, можете вставить.
На первом рисунке поикано разложение скорости в обеих системах координат. Скорость всегда направлена по касательной к траектории по направлению движения частицы. Проекция VR направлена по направлению вектора R, проекция Vφ перпендикулярна ему. На данном рисунке обе проекции положительны. Проекция Vx отрицательна.
На втором рисунке показано разложение ускорения. Кроме аналогичного разложения на проекции по координатным осям, показано его разложение на нормальное и тангенциальное компоненты. Первое направлено по направлению радиуса кривизны траектории, второе перпендикулярно ему. На рисунке скорость и тангенциальное ускорение совпадают по направлению. Следовательно, скорость увеличивается. Никогда не путайте радиус кривизны Rc с радиус-вектором R. Хорошо видно, что это совершенно разные вектора. Первый
начинается в центре кривизны траектории в данной точке и заканчивается в точке нахождения частицы, второй начинается в начале координат и заканчивается в точке нахождения частицы. Обратите внимание, на рисунке показан отрезок вектора Rc (знак минус поставлен, чтобы подчеркнуть, что радиус кривизны имеет противоположное направление стрелки, показанной на рисунке). Орт n направлен к центу кривизны, то есть его направление противоположно Rc. Орт τ всегда по направлению совпадает с V.
PDF created with pdfFactory Pro trial version www.pdffactory.com

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
1. Примеры решения задач на законы Ньютона.
1.Наклонная плоскость.
Определить, как будут двигаться тела, показанные на рисунке. Шнур невесом и нерастяжим. Трение между шнуром и закругленной частью клина отсутствует. Считать
величины m1 , m2 , k - коэффициент трения между телом и поверхностью клина, α . При t=0
тела покоились.
Решение.
1. Делаем рисунок (он показан). Выбираем оси координат. Для этой
задачи удобней выбрать две системы. Ось x удобней направить вверх, если ось y′ направлена
вниз, чтобы оба тела двигались в положительном (либо в отрицательном) направлениях.
2. Расставляем на рисунке все силы.
3. Для каждого тела пишем уравнение
движения в векторном виде:
m1a1 = m1 g +T1 + N + Fтр
m2a = m2 g +T2
4. Расписываем уравнения в проекциях на координатные оси (для каждого тела): m1ax1 = T1 − m1g sinα − Fтр
m1ay1 |
= N − m1g cosα |
(3) |
m2ay′2 = m2 g −T2 |
|
|
Пишем дополнительные уравнения, столько, чтобы полное число линейно независимых уравнений равнялось числу неизвестных величин.
Так как ay1 =0, то N = m1g cosα . Выражаем |
силу |
трения: Fтр = kN = km1gcosα . Из |
невесомости шнура следует равенство: T1 = T2 |
= T . |
Из нерастяжимости шнура следует |
соотношение: ax1 = ay′2 . Переписываем уравнения (3) с учетом полученных соотношений:
m1ax1 = T − km1g cosα − m1g sinα |
(4) |
m2ay′2 = m2 g −T , ( ax1 = ay′2 ) |
|
Два уравнения с двумя неизвестными: ax1 (или ay′2 ) и T . Вот теперь их можно решать. Складывая их, находим ускорения тел:
= = m − m (sinα + k cosα)
ax1 ay′2 2 1 m1 + m2 g (5)
Это решение имеет смысл, если числитель дроби положителен. Если он отрицателен, то надо решать практически другую задачу, так как, начиная с рисунка все надо менять.
Проделаем это. Теперь сила трения
направлена вверх по наклонной плоскости. Обратите внимание на то, что я изменил направления осей (так проще, но можно и по Чехову: «забивать гвоздь от противоположной стенки»*). Векторные уравнения движения не изменяться. Так как
дополнительные уравнения не
PDF created with pdfFactory Pro trial version www.pdffactory.com
изменяться, то сразу напишу систему (4) для рассматриваемого случая:
|
m1ax1 = m1g sinα -T - km1g cosα |
||
|
|
m2ay′2 = T - m2 g |
|
Складывая, находим ускорения тел: |
|||
ax1 |
= ay′2 = |
m1 sinα - (m2 + km1 cosα) |
g (6) |
|
|||
|
|
m1 + m2 |
|
Из (5) и (6) следует, что при выполнении неравенств:
sinα - k cosα £ m2 £ sinα + k cosα m1
тела будут покоиться.
Так как все величины, определяющие ускорения тел, постоянны, то движение тел в обоих случаях будет равноускоренным (до того момента пока одно из тел не упрется в выступ). Скорость, например, первого тела находится интегрированием ускорения по времени:
òdvx1 = òax1dt Þ vx1 = ax1t + Const
Постоянная равна нулю, так как в начальный момент тела не двигались. Повторным интегрированием находим перемещение тела:
òdx = òvx1dt = òax1tdt Þ x = |
a |
t2 |
+ Const |
|
x1 |
||
|
|
2 |
|
Величина постоянной зависит от выбора положения начала координат, так как она равна координате тела в начальный момент времени. Перемещение тела не будет зависеть от выбора и будет равно:
Dx = x(t) - x(0) = ax1t2 2
Аналогично находятся скорость и перемещение второго тела.
* Психбольница. Одному психу велели повесить картину. Он взял гвоздь, приставил шляпку к стенке, а по острию стал бить молотком. Подходит санитар и говорит: «Что же ты делаешь, дурак. Этот гвоздь от противоположной стенки».
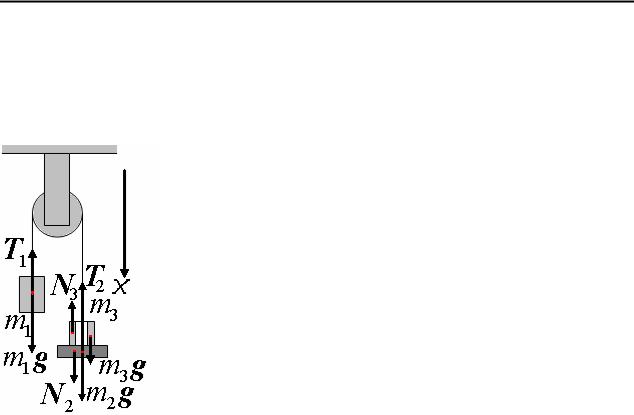
2. Блок. На невесомом шнуре подвешены три тела с известными массами. Суммарная масса справа больше левой (см. рис.). Трение отсутствует. Найти с какой силой давит третье тело на второе во время движения.
Решение.
Рисунок сделан. Силы расставлены. Для наглядности для двух грузов силы разнесены. Правильнее их все надо направить по шнуру, но тогда они сольются. Далее надо написать уравнения движения для каждого тела в векторном виде. Обязательно напишите сами. Затем следует эти уравнения написать в
проекциях на ось x:
m1&&x1 = m1 g -T1
m2&&x2 = m2 g + N2 -T2 m3&&x3 = m3g - N3
Я не стал обозначать ускорения буквой а, чтобы не писать два индекса. Неизвестных семь, уравнений всего три. Надо найти еще четыре уравнения. Первое уравнение следует из третьего закона Ньютона:
N2 = N3 = N
Из невесомости шнура следует равенство:
PDF created with pdfFactory Pro trial version www.pdffactory.com

T1 = T2 = T
Из нерастяжимости шнура следует еще два равенства:
&&x3 = &&x2 = −&&x1
Перепишем систему уравнений движения с учетом полученных соотношений:
m1&&x1 = m1g −T
m2&&x2 = m2 g + N −T m3&&x3 = m3 g − N
Так как нам надо найти силу давления, то ускорения тел и силу натяжения следует исключить из уравнений. Если из второго вычесть первое, то получим:
(m2 + m1)&&x2 = (m2 − m1)g + N
Не поленимся и перепишем два оставшихся уравнения, разрешенных относительно ускорений:
&&x2 = (m2 − m1)g + N
(m2 + m1)
&&x3 = m3gm− N
3
Левые части равны, следовательно, равны правые:
(m2 − m1)g + N = m3g − N m3
Разрешив его относительно N , найдете ответ.
Это решение задачи, так сказать, по общей схеме. Можно решить и короче. Для этого два тела m2 и m3 представить как одно с массой m2 + m3 . Тогда останутся два уравнения
движения:
m1&&x1 = m1g −T1
(m2 + m3 )&&x2 = (m 2 +m3 )g −T2
Используя те же дополнительные уравнения, получим:
−m1&&x2 = m1g −T
(m2 + m3 )&&x2 = (m2 + m3 )g −T
Вычтя из второго первое, находим ускорение, с которым двигается второе тело:
&&x2 = (m2 + m3 ) − m1 g m1 + m2 + m3
Напишем уравнение движения для третьего тела:
m3&&x3 = m3 g − N
Из этого уравнения находим силу, действующую на третье тело со стороны второго (ускорение второго тела равно ускорению второго, которое мы перед этим определили):
N = m3 (1− (m2 + m3 ) − m1 )g m1 + m2 + m3
По третьему закону Ньютона с такой же силой третье тело давит на второе. Следовательно, искомая сила равна:
N = |
|
2m1m3 |
|
g . |
m + m + m |
||||
1 |
2 |
3 |
|
|
На мой взгляд, второе решение проще.
ЗАКОНЫ СОХРАНЕНИЯ
1. Первый интеграл уравнения движения. Кинетическая энергия. Работа.
Хорошо известно, что для определения характера движения тела (если его можно считать материальной точкой) определяется интегрированием Второго закона Ньютона по времени. Из первого интегрирования определяется скорость тела как функция
PDF created with pdfFactory Pro trial version www.pdffactory.com
времени, из второго-его координаты. Для однозначного определения этих величин должны быть известны начальные условия.
Проинтегрируем уравнение Второго закона Ньютона не по времени, а по координатам.
Для этого обе части уравнения движения умножим скалярно на бесконечно малое приращение dr :
m dv dr = F (r)dr |
2 |
2 |
mvdv = F (r)dr mòvdv = òF (r)dr |
||
dt |
1 |
1 |
Под пределами интегрирования надо понимать либо скорости, либо координаты тела в начальном и конечном положениях. Левую часть последнего равенства можно проинтегрировать в общем случае, правую часть не зная зависимость силы от координат нельзя. Таким образом, получаем:
2 |
2 |
|
|
|
|
|
|
v2 |
|
vy2 |
|
v2 |
|
|
v2 |
|
v2 |
|
òvdv = ò(vxdvx + vydvy + vz dvz ) = [ |
x |
+ |
|
+ |
z |
]12 |
= |
2 |
- |
1 |
||||||||
2 |
||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
2 |
||
|
mv2 |
- |
mv2 |
= |
2 |
|
|
|
(7) |
|
|
|
|
|
||||
|
2 |
|
1 |
òF(r)dr |
|
|
|
|
|
|
|
|||||||
Величина |
2 |
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Eк |
= |
mv2 |
|
|
|
(8) |
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По определению называется кинетической энергией, правая часть есть работа. Таким образом, приращение кинетической энергии тела равно работе всех сил, приложенных к этому телу:
Eк2 - Eк1 = A12 |
(9) |
Обратите внимание на расстановку индексов. Следует заметить, что приращение энергии будет отрицательным, если работа отрицательна, например работа сил трения.
Может возникнуть вопросы. А как вычислить работу, если неизвестна траектория движения тела? Если мы ее найдем из интегрирования уравнения движения по времени, то тогда будут известны и скорость тела в любой момент времени. Тогда какой прок от уравнения (2)? Вопросы законные. Действительно в этом случае прока нет. Но в природе есть силы, работа которых не зависит от траектории тела, а определяется только конечным и начальным положением тела. Или, что одно и то же, работа таких сил по любому замкнутому контуру равна нулю. Такие силы называются консервативными. Для консервативных сил уравнение (3) позволяет решать задачи много проще. Прежде, чем двигаться дальше, получим критерий консервативности сил.
2. Критерий консервативности силы.
Пусть в некоторой области пространства имеется поле консервативной силы. Выберем в произвольной точке начало координат и выделим кубик размером x, y, z. Вычислим работу силы, при перемещении по ребрам кубика вокруг грани, расположенной в плоскости XY. Обход будем совершать по часовой стрелке. Если сила консервативная, то работа должна быть равна нулю (замкнутый контур):
DA = Fy (x)Dy + Fx (y + Dy)Dx - Fy (x + Dx)Dy - Fx (y)Dx = 0 |
||||||||||||
Преобразуем это выражение к виду: |
|
Fy (x + Dx) - Fy |
(x) |
|
||||||||
DA = |
F ( y + Dy) - F (y) |
DxDy - |
DxDy = 0 |
|||||||||
x |
|
|
x |
|
|
|
|
|
||||
Dx |
|
|
|
|
Dy |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
В пределе при x и |
y, стремящихся |
к нулю, получим |
|
соотношение для частных |
||||||||
производных: |
|
|
|
|
¶Fy |
|
|
|
¶Fy |
|
|
|
|
δ А = ( |
¶F |
|
|
)DxDy = 0 Þ |
¶F |
|
|
||||
|
x |
- |
|
|
x = |
|
|
. |
|
|||
|
|
¶x |
¶x |
|
|
|||||||
|
|
¶y |
|
|
|
|
¶y |
|
|
|
||
Приведенный вывод следует пояснить, так как изложение необходимого материала по математике для физики почти всегда отстает. Что такое частная производная? Будет понятнее, если рассмотреть хорошо известный пример. При прямолинейном, равноускоренном движении тела (без начальной скорости) путь, пройденный телом равен:
PDF created with pdfFactory Pro trial version www.pdffactory.com

S = at22 .
Если от этого выражение найти производную по времени, получим скорость тела. Однако при этом молчаливо предполагается, что ускорение тела постоянно и путь является только функцией времени. Однако мы можем считать, что путь является функцией двух переменных: времени и ускорения. Мы можем взять производную по ускорению, считая время постоянной величиной, и получить прямую пропорциональность пути ускорению t2/2. От функции нескольких переменных можно взять производную по каждой переменной, считая остальные переменные постоянными. Чтобы подчеркнуть это d пишется закругленным.
Вам известно, что дифференциал (бесконечно малое приращение) функции одной переменной имеет вид:
dF = Fx/ dx = dFdx dx
Дифференциал функции нескольких переменных, например трех, равен:
dF = |
∂F dx + |
∂F dy + |
∂F dz |
(10) |
|
∂x |
∂y |
∂z |
|
Вернемся к основному материалу. Мы рассмотрели работу силы по контуру, лежащим в плоскости XY. Совершенно очевидно, что мы получим аналогичные соотношения для частных производных, если рассмотреть еще два контура в других плоскостях. Выпишем для трехмерного пространства условие консервативности силы:
∂F |
∂Fy |
|
∂Fy |
|
∂F |
∂F |
∂F |
|
x = |
|
|
|
= |
z |
z = |
x |
(11) |
∂x |
|
∂z |
||||||
∂y |
|
|
∂y |
∂x |
∂z |
|
Полученные соотношения являются дифференциальными, то есть они должны выполняться в каждой точке пространства поля консервативной силы. Если, для простоты, ограничиться плоским произвольным контуром, то его можно разбить на элементарные ячейки, Можно все ячейки проходить в одном направлении. Работа по всем ячейкам естественно будет равна нулю, По внутренним сторонам между ячейками мы проходим дважды, навстречу, и так как работа в одном направлении равна такой же работе, но со знаком минус, то сумма их равна нулю. Таким образом, внутренние перемещения можно откинуть. Остается работа по внешнему контуру, причем перемещение происходит в одном направлении, и эта работа равна нулю. Из этого следует интегральное определение консервативности силы, через равенство нулю работы по замкнутому контуру.
3. Оператор набла.
Перейдем к рассмотрению правой части уравнения (1). Силу, стоящую под интегралом надо понимать как сумму всех сил, приложенных к телу. Разобьем это выражение на сумму двух:
2 2 2
òFdr =òFc dr + òF* dr (12)
1 1 1
Второе слагаемое представляет собой работу неконсервативных сил. Первое-работу консервативных сил. Так как величина этого интеграла зависит только от значений координат в начальной и конечной точках, то, следовательно, под интегралом стоит полный дифференциал некоторой функции. В общем случае, эта функция трех координат: x, y, z. Удобнее ввести дифференциал со знаком минус (в дальнейшем это станет ясно). Для удобства сними индекс. Все дальнейшее будет только для консервативных сил. Таким образом:
2 |
2 |
|
òFdr = − òdU |
(13) |
|
11
Влевой части распишем скалярное произведение двух векторов:
2 |
2 |
2 |
2 |
2 |
|
òFdr =ò(Fxdx + Fydy + Fz dz) = òFxdx + òFy dy + òFz dz |
(14) |
||||
1 |
1 |
1 |
1 |
1 |
|
В правой - полный дифференциал (5)
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
2 |
|
2 |
|
2 |
|
|
2 |
|
|
|
-òdU = -ò |
¶U dx - ò ¶U dy - ò ¶U dz : |
||||||||||
|
1 |
|
1 |
¶x |
1 |
¶y |
1 |
¶z |
|||
Из сравнения (13) и (14) следует: |
|
|
¶U |
|
|
|
|
||||
F = - |
¶U |
|
F = - |
|
F = - |
¶U |
|||||
|
|
|
|||||||||
x |
|
¶x |
|
|
y |
¶y |
z |
|
¶z |
||
|
|
|
|
|
|
|
|
||||
(15)
(16)
Умножив эти выражения на соответствующие орты и сложив, получим: |
|
|
|
|||||||||||
e F + e F + e F = -e |
¶U - e |
¶U |
- e |
¶U |
= -(e |
|
¶ |
+ e |
|
¶ |
+ e |
|
¶ |
)U |
y ¶y |
z ¶z |
x ¶x |
y ¶y |
|
||||||||||
x x y y z z |
x ¶x |
|
|
|
|
z ¶z |
||||||||
F = ÑU |
|
|
|
(17) |
|
|
|
|
|
|
|
|
||
В последнем выражении перевернутым треугольником обозначено выражение, стоящее в скобках в строчке выше. Этот символ называется оператором набла, причем здесь он записан в декартовых координатах (ниже покажу, как его надо писать в других системах координат). Что такое оператор? Это просто правило, что надо сделать с функцией, стоящей после него. Обозначения тригонометрических функций (sin, cos т.д.) тоже в какам-то смысле можно считать операторами. Ведь подействовав на некоторую функцию F(x) мы получаем сумму членов бесконечного ряда, которые пишутся по определенному правилу.
Сам оператор без стоящего за ним выражения смысла практически не имеет. Важно понимать, что оператор дифференциальный. Поэтому, если после него стоит константа, то эта комбинация тождественно равна нулю. Если после него стоит скалярная функция, то эта комбинация называется градиентом функции. Кроме того, оператор векторный. Так как вектор можно умножить на другой вектор как скалярно, так и векторно, то мы будем иметь два разных правила «воздействия» оператора на вектор и получим два разных результата. Из-за важности сказанного выпишем это в виде формул:
ÑConst = 0
ÑF(x, y, z) = ex ¶F + ey ¶F + ez ¶F ¶x ¶y ¶z
Если функция зависит только от одной переменной (например, от x), то
ÑF(x) = e |
|
¶F |
= e |
dF |
|
x |
¶x |
x dx |
|||
|
|
Скалярное произведение:
ÑG(x, y, z) = ¶¶Gxx + ¶¶Gyy + ¶¶Gzz
Векторное произведение:
[ÑG(x, y, z)] = (ex ¶¶x + ey ¶¶y + ez ¶¶z)(exGx + eyGy + ezGz )
В последней строчке надо выполнить умножение по правилу перемножения многочленов. Нам сейчас последние выражения не будут нужны, и я доводить вычисления до конца не буду.
Мы будем иметь дело с полями сил, имеющих цилиндрическую или сферическую симметрию. В таком случае надо уметь выразить оператор набла в соответствующих системах координат. Я сейчас покажу прием, как это сделать. Оператор состоит из трех слагаемых по числу ортов ортогональной системы координат. В каждом слагаемом в числители стоит круглое d , а в знаменателе бесконечно малое приращение по соответствующей оси. Теперь по подобию пишем оператор в цилиндрической и сферической системах координат:
Ñ = e |
|
¶ |
+ e |
¶ |
+ e |
|
¶ |
R ¶R |
|
z ¶z |
|||||
|
ϕ R¶ϕ |
|
|||||
¶
r sinθ¶ϕ
Для полей, независящих от углов, то есть обладающих осевой или сферической симметрией (зависящих только от расстояния от оси R или от расстояния от начала координат r) будем в обоих случаях иметь только член, причем полную производную:
PDF created with pdfFactory Pro trial version www.pdffactory.com
ÑF(R) = e |
dF |
ÑF(r) = e |
dF |
(18) |
|
R dR |
r |
dr |
|
4. Потенциальная энергия. Полная энергия. |
||||
Закон сохранения полной энергии. |
|
|||
В предыдущем параграфе получены очень нужные формулы. |
Но до сих пор был просто |
|||
математический формализм. Теперь перейдем к физике. Введенная функция U называется потенциальной энергией. Следует обратить внимание на то, что потенциальная энергия определяется с точностью до произвольной постоянной. Когда поле сил на бесконечности стремиться к нулю (например, гравитационное поле Земли или поле точечного заряда) эту постоянную принято выбирать равной нулю. Из выводов в предыдущем параграфе следует, что убыль (приращение со знаком минус) потенциальной энергии равно работе консервативных сил. Так как всегда определяется разность потенциальной энергии, то величина произвольной постоянной несущественна. Полученные выражения (16) и (17) связывают консервативную силу с потенциальной энергией (локально, в каждой точке).
Уравнение (7) с учетом (12) и (13) принимает вид: |
|
|
||
mv2 |
mv2 |
2 |
2 |
|
2 - |
1 |
= -òdU +òF* (r)dr |
|
|
2 |
2 |
1 |
1 |
|
|
|
2 |
|
|
E2 - E1 = (Eк2 +U2 ) - (Eк1 +U1) = òF* (r)dr |
(19) |
|||
Величина |
|
1 |
|
|
|
|
|
|
|
Е = Eк +U |
|
(20) |
|
|
называется полной механической энергией.
Таким образом, при отсутствии неконсервативных сил полная энергия сохраняется:
Е1 = E2
Последнее выражение называется законом сохранения полной механической энергии.
5. Энергия взаимодействия.
Начнем с простого примера. Точечное тело находится в поле сил тяжести Земли. На него действует сила:
F (z) = -ez mg |
|
|
(21) |
|||
Ось Z направлена от центра земли, Начало координат выберем на поверхности земли. |
||||||
Напишем уравнение (16) для рассматриваемого примера: |
||||||
e |
|
dU |
= e |
mg |
dU |
= mg |
|
z |
dz |
z |
|
dz |
|
Интегрируя, находим потенциальную энергию тела: |
|
|
||||
U = mgz + const |
|
(22) |
||||
Все это верно, если тело находится на высоте |
|
|
||||
H << R |
|
|
|
|
(23) |
|
где R-радиус Земли.
Если снять ограничение (23), то сила притяжения к земле, согласно закону всемирного тяготения Ньютона, равна:
F (r) = -e |
G Mm |
(24) |
z |
r2 |
|
а потенциальная энергия находится интегрированием выражения:
dU |
= G Mm |
(25) |
dr |
r2 |
|
Проинтегрировав по r, находим |
|
|
U = -G Mm + const |
(26) |
|
r
-потенциальную энергию тела в гравитационном поле Земли. Но можно считать и наоборот, что это потенциальная энергия Земли в гравитационном поле тела. Все зависит от того, что мы считаем внешним телом, а что телом нашей системы. Если оба тела являются телами
PDF created with pdfFactory Pro trial version www.pdffactory.com
