3. Кривые второго порядка. Канонические ур-ия эллипса, гиперболы и параболы. Каноническое уравнение эллипса.

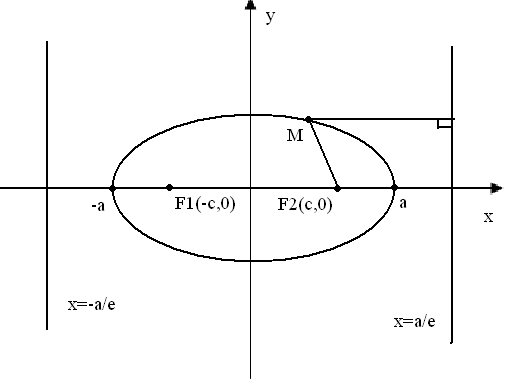
ОПР: Эллипсом называется геометрическое место точек, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2а, большее, чем расстояние между фокусами=2с (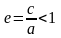 - эксцентриситет эллипса). F₁M+F₂M=2a, где M – любая точка эллипса.

F₁, F₂ – фокусы эллипса; расстояние между F₁, F₂, равное 2с – фокусное расстояние; а – большая полуось; О – середина F₁F₂ – центр эллипса, F₁F₂ – первая (фокальная) ось; прямая, проходящая через О  F₁F₂ – вторая ось.

Теорема: Каноническое уравнение эллипса имеет вид

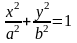
► Из неравенства треугольника:

F₁M+F₂MF₁F₂. При a=c, точка М принадлежит [F₁,F₂], при a>c , точка М не принадлежит [F₁,F₂].

Дан эллипс. Построим его каноническое уравнение. Введем систему координат. Начало возьмем совпадающее с центром эллипса, ось абсцисс направим по фокальной оси, ось ординат направим по второй оси.

F₁=(-с,0), F₂=(с,0), М=(x,y)

F₁M+F₂M=2a ,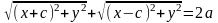

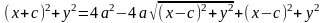
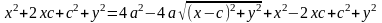
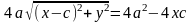
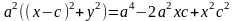
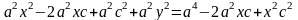
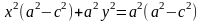, по определению

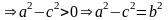
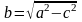, b – малая полуось.

- каноническое уравнение эллипса.

Докажем, что если точка (х, у) удовлетворяет полученному уравнению, то она принадлежит эллипсу, то есть r₁+r₂=2a, где r₁, r₂ – фокальные радиусы. .

Из уравнения получим 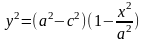, и подставим значение y² в r₁.

Получим .

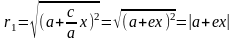Из уравнения 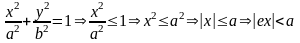(так как 0<e<1).

Тогда a+ex<a+ex.

Аналогично a-ex<a-ex.

Тогда r₁+r₂= a+ex +a-ex =2a. ◄

Каноническое уравнение гиперболы.

ОПР: Гиперболой называется геометрическое место точек, модуль разности расстояний каждой из которых до двух данных точек – есть положительное и постоянное число 2а. F₁M-F₂M=2a, где M – любая точка гиперболы.

F₁, F₂ – фокусы гиперболы; расстояние между F₁, F₂, равное 2с – фокусное расстояние; а – большая полуось; О – середина F₁F₂ – центр гиперболы; F₁F₂ – первая (действительная) ось; прямая, проходящая через О  F₁F₂ – вторая (мнимая) ось.

Эксцентриситет гиперболы

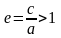
Т еорема: Каноническое уравнение гиперболы имеет вид:

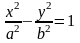
►F₁M-F₂MF₁F₂.

Дана гипербола. Построим ее каноническое уравнение. Введем систему координат. Начало возьмем совпадающее с центром гиперболы, ось абсцисс направим по фокальной оси, ось ординат направим по второй оси.

Тогда F₁=(-с,0), F₂=(с,0), М=(x,y)

 ,

,

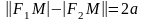
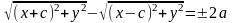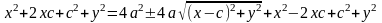
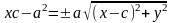
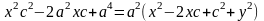
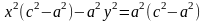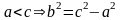
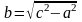, b – малая полуось.

- каноническое уравнение гиперболы.

Докажем, что если точка (х, у) удовлетворяет полученному уравнению, то она принадлежит гиперболе, то есть r₁+r₂=2a, где r₁, r₂ – фокальные радиусы. .

Из уравнения получим 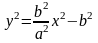, и подставим значение y² в r₁.

Получим .

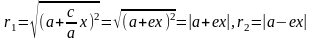Из уравнения .

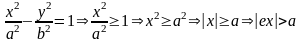1. x0, тогда r₁=а+ех, r₂= -(а-ех), r₁-r₂= 2a.

2. x<0, тогда r₁= -а-ех, r₂= а-ех, r₁-r₂= 2a. ◄

Каноническое уравнение параболы.

ОПР: Параболой называется геометрическое место точек плоскости, отношение расстояний от которых до некоторой точки F (фокуса) и до некоторой прямой d (директриса) постоянно. М – любая точка параболы.

Теорема: Каноническое уравнение параболы имеет вид у²=2рх

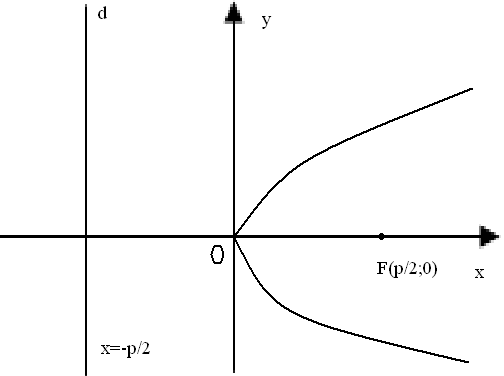
►Дана парабола. Построим ее каноническое уравнение. Введем систему координат. Начало возьмем в середине отрезка DF. D – точка пересечения директрисы d и прямой, перпендикулярной d, проходящей через F. За ось абсцисс примем DF, за ось ординат – прямую, перпендикулярную оси абсцисс, проходящую через О. Обозначим p – расстояние между F и d. Тогда F=(p/2,0). Уравнение директрисы d: x= -p/2.

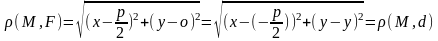
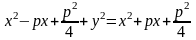
у²=2рх – каноническое уравнение параболы. Заметим, что р>0, значит х0.

Докажем, что если точка М=(х, у) удовлетворяет полученному уравнению, то она принадлежит параболе. Рассмотрим точку F=(р/2, 0) и прямую d: х = -р/2.

(М, d)=х+р/2=х+р/2, .◄
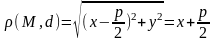