
- •А.В. Даниленков
- •Тема 1. Предмет, метод и задачи статистической науки.
- •Тема 2. Задачи и принципы организации государственной статистики в рф
- •Тема 3. Статистическое наблюдение
- •Тема 4. Сводка и группировка статистических данных
- •Тема 6. Способы наглядного представления статистических данных
- •Тема 7. Абсолютные и относительные величины
- •Тема 8. Средние величины и показатели вариации в статистике
- •Тема 9. Выборочное наблюдение
- •Тема 10. Ряды динамики и их применение в анализе социально-экономических явлений
- •Тема 11. Индексы
- •Статистика опорный конспект лекций по дисциплине для специальностей 080114 «Земельно-имущественные отношения»,
- •080501 «Менеджмент»
- •Составитель а.В. Даниленков
Тема 11. Индексы
Индекс в переводе с латинского означает показатель. Индексом называется относительная величина, характеризующая изменение сложных экономических явлений по времени, в пространстве и в то же время уровень планового задания и степень выполнения плана.
При помощи индексов можно характеризовать изменения самых различных показателей: цен, себестоимости, товарооборота, численности работающих, производительности труда, заработной платы и т.д.
Исчисление общих индексов, позволяющих соотносить между собой показатели по сложным совокупностям, составляет приём исследования именуемый индексным методом. Под сложной совокупностью, понимается такая совокупность, отдельные элементы которой не подлежат непосредственному суммированию.
Индексный метод позволяет определить влияние отдельных факторов на изменение показателя.Индексный анализ применяется для изучения явления во времени, по территориям, а также для определения влияния факторов на изменение обобщающего показателя.
Индексы позволяют решить следующие задачи:
Определить изменение простого явления во времени. Для этого используются индивидуальные индексы, которые равны соотношению уровня явления в отчетном и базисном периодах:
![]() .
.
Определить изменение сложного явления во времени. С этой целью применяют сводные (агрегатные) индексы. В зависимости от базы, на которой фиксируются соизмерители, различают индексы Пааше, Ласпейреса, Фишера, Лоу.
Индекс Пааше (соизмеритель на отчетном уровне):
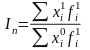
где
![]() - уровень индексированной величины в
отчетном и базисном периодах;
- уровень индексированной величины в
отчетном и базисном периодах;
![]() -
уровень соизмерителя в отчетном периоде.
-
уровень соизмерителя в отчетном периоде.
б) Индекс Ласпейреса (соизмеритель на базисном уровне):
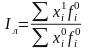
где
![]() - уровень соизмерителя в базисном
периоде.
- уровень соизмерителя в базисном
периоде.
в) Индекс Лоу (соизмеритель - средняя из уровней отчетного и базисного периодов):
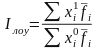
где
![]() .
.
г) Индекс Фишера (равен средней из индексов Пааше и Ласпейреса)
![]()
Определить влияние факторов на динамику сложных явлений. Для этого используется система взаимосвязанных индексов.
-
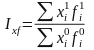 Показывает
общее изменение изучаемого показателя
Показывает
общее изменение изучаемого показателя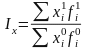 Показывает
изменение изучаемого показателя за
счет изменения качественного признака
Показывает
изменение изучаемого показателя за
счет изменения качественного признака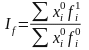 Показывает
изменение изучаемого показателя за
счет количествен-ного признака
Показывает
изменение изучаемого показателя за
счет количествен-ного признака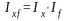 ,
,
где
![]() - значения качественного показателя в
базисном и отчетном периодах;
- значения качественного показателя в
базисном и отчетном периодах;
![]() -
значения количественного показателя
в базисном и отчетном периодах.
-
значения количественного показателя
в базисном и отчетном периодах.
Определить изменение среднего значения признака и рассчитать влияние факторов на его изменение. С этой целью используют систему индексов постоянного, переменного состава и индекс структурных сдвигов.
а) Индекс переменного состава показывает общее изменение среднего значения признака:
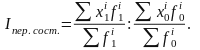
б) Индекс постоянного состава позволяет определить влияние изменения осредняемого признака на общее изменение средней:
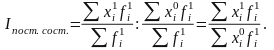
в) Индекс структурных сдвигов отражает изменение средней под воздействием изменения структуры совокупности:
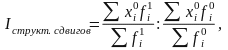
Iпер. состава = Iпост. сост. · Iструкт. сдвигов,
где
![]() - значения осредняемого признака в
базисном периоде;
- значения осредняемого признака в
базисном периоде;
![]() -
значения
осредняемого признака в отчетном
периоде;
-
значения
осредняемого признака в отчетном
периоде;
![]() -
вес осредняемого признака в отчетном
и базисном периодах.
-
вес осредняемого признака в отчетном
и базисном периодах.
Для определения среднего индекса из индивидуальных используют средний арифметический и средний гармонический индексы.
Средний
арифметический индекс применяется в
том случае, если известен уровень
обобщающего явления в базисном периоде
(![]() )
)
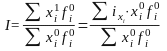 ,
,
так
как из формулы (1)
![]() .
.
Средний гармонический индекс используется тогда, когда известен уровень обобщающего явления в отчетном периоде (x1f1) и получается путем преобразования в средний агрегатного индекса Пааше.
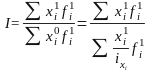 ,
,
где
![]() - индивидуальные индексы;
- индивидуальные индексы;
![]() -
значения обобщающего показателя в
базисном и отчетном периодах.
-
значения обобщающего показателя в
базисном и отчетном периодах.
