
- •Теорія механізмів і машин
- •Передмова
- •Розділ 1. Самостійна робота над теоретичною частиною курсу
- •1.1. Модуль 1. Вступ. Структурний аналіз механізмів
- •1.2. Модуль 2. Кінематичне дослідження важільних механізмів
- •1.3. Модуль 3. Кінематичне дослідження зубчастих механізмів
- •1.4. Модуль 4. Динаміка механізмів і машин Вступ до динамічного дослідження механізмів
- •Силовий аналіз механізмів
- •Аналіз руху механізмів і машин
- •Зрівноважування і віброзахист механізмів
- •1.5. Модуль 5. Синтез механізмів кулачкові механізми
- •Теорія зубчастих зачеплень
- •Розділ 2. Модуль 1. Структурний аналіз і класифікація механізмів
- •2.1. Основні поняття структурного аналізу
- •2.2. Приклади структурного аналізу механізмів
- •2.3. Завдання зі структурного аналізу механізмів
- •Розділ 3. Модуль 2. Кінематичне дослідження важільних механізмів
- •3.1. Приклади визначення швидкостей та прискорень методом планів
- •3.2 Завдання з побудови планів швидкостей та прискорень
- •3.3. Побудова крайніх положень механізмів
- •4.2. Завдання зі знаходження передаточних відношень механізмів з нерухомими та рухомими осями
- •4.3. Завдання для визначення передаточних відношень послідовно з'єднаних передач
- •Розділ 5. Модуль 4. Силовий аналіз механізмів
- •5.1. Приклади силового аналізу
- •5.2. Завдання з силового аналізу
- •Розділ 6. Модуль 5. Синтез планетарних передач
- •6.1. Синтез планетарних механізмів
- •2. Передача, складена з двох однорядних механізмів
- •6.2. Завдання з синтезу планетарних механізмів
- •7.2. Завдання з геометричного синтезу нерівнозміщеного евольвентного зачеплення
- •Розділ 8. Тестовий контроль знань студентів
- •8.1. Тестовий контроль за перше півріччя навчального року
- •8.2. Тестовий контроль за друге півріччя
- •Список Літератури
8.2. Тестовий контроль за друге півріччя
Модуль 3. Кінематичне дослідження механізмів зубчастих передач
Питання 47
100 |
За якою формулою визначається передаточне відношення даного зубчастого механізму? У формулах m – кількість зовнішніх зачеплень; zi – кількість зубів і–того колеса, і = 1, 2, 3,...
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 48
100 |
За якою формулою визначається передаточне відношення цього зубчастого механізму? У формулах m – кількість зовнішніх зачеплень; zi – кількість зубів і–того колеса, і = 1, 2, 3,...
|
1 |
|
2 |
. |
3 |
. |
4 |
|
Питання 49
75 |
Чому дорівнює передаточне відношення кількох послідовно з’єднаних зубчастих передач? |
1 |
Сумі передаточних відношень передач, які входять до складу з’єднання. |
2 |
Сумі чисел зубів коліс, які входять до складу з’єднання. |
3 |
добутку передаточних відношень кожної окремої передачі, які входять до складу з’єднання. |
4 |
добутку чисел зубів коліс передач, які входять до складу з’єднання. |
Питання 50
100 |
Навести формулу для визначення передаточного відношення показаного зубчастого механізму. У формулах m – кількість зовнішніх зачеплень; zi – кількість зубців і–того колеса, і = 1, 2, 3,...
|
1 |
|
2 |
|
3 |
|
4 |
. |
Питання 51
75 |
Чому дорівнює ступінь рухомості планетарних зубчастих механізмів? |
1 |
4 |
2 |
3 |
3 |
2 |
4 |
1 |
Питання 52
100 |
Вибрати формулу для визначення передаточного відношення цієї зубчастої передачі. У формулах m – кількість зовнішніх зачеплень; zi – кількість зубців і–того колеса, і = 1, 2, 3,...
|
1 |
|
2 |
|
3 |
. |
4 |
|
Питання 53
75 |
Чому дорівнює ступінь рухомості диференціальних зубчастих механізмів? |
1 |
2, 3, 4, ... |
2 |
1 |
3 |
числу зубчастих коліс. |
4 |
Числу зовнішніх зачеплень. |
Питання 54
100 |
За якою формулою визначається передаточне відношення даного зубчастого механізму? У формулах m – кількість зовнішніх зачеплень; zi – кількість зубців і–того колеса, і = 1, 2, 3,...
|
|
1 |
. |
|
2 |
. |
|
3 |
. |
|
4 |
. |
|
Питання 55
100 |
За якою формулою визначається передаточне відношення даного зубчастого механізму? У формулах zi – кількість зубів і–того колеса, і = 1, 2, 3,...
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Питання 56
100 |
За якою формулою визначається передаточне відношення даного зубчастого механізму? У формулах zi – кількість зубів і–того колеса, і = 1, 2, 3,...
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
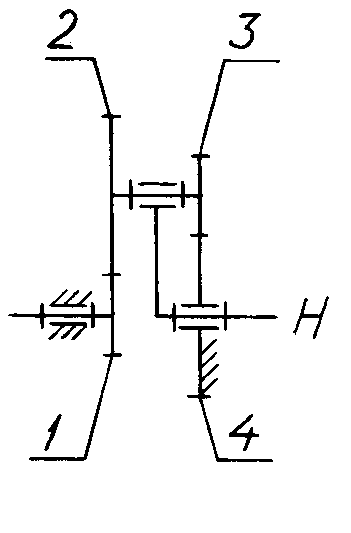
Питання 57
100 |
Навести формулу
вілліса
для диференціалів. колеса
1, n
і водило Н
обертаються з кутовими швидкостями
|
1 |
|
2 |
|
3 |
|
4 |
|
Модуль 4. Динаміка механізмів і машин
Питання 58
75 |
Якою є задача силового аналізу механізмів? |
1 |
Коли відомі сили, які діють на механізм, знаходять рух його ланок. |
2 |
Коли відомі сили, які діють на механізм, знаходять прискорення його ланок. |
3 |
У ній по заданому закону руху початкової ланки визначають зовнішні сили, які забезпечують цей рух. |
4 |
Коли відомі сили, які діють на механізм, знаходять швидкості його ланок. |
Питання 59
75 |
Якою є задача динаміки механізмів і машин? |
1 |
Коли відомий рух механізму, визначають зовнішні сили. |
2 |
У ній по заданому закону руху початкової ланки визначають зовнішні сили. |
3 |
у ній по заданим зовнішнім силам визначається закон руху початкової ланки. |
4 |
Коли відомий рух механізму, визначають прискорення початкової ланки. |
Питання 60
75 |
механічними характеристиками машин називаються залежності: |
1 |
кінематичних параметрів від часу, швидкості, шляху. |
2 |
швидкостей та прискорень від часу та шляху. |
3 |
рушійних сил та сил опору від часу, швидкості, шляху та інших величин. |
4 |
реакцій в кінематичних парах від часу, швидкості, шляху. |
Питання 61
75 |
Навести векторне
рівняння рівноваги показаної на
рисунку групи ланок 4 – 5. До групи
прикладені: зовнішня
сила корисного опору
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 62
50 |
Як виглядає
векторне рівняння рівноваги кривошипа,
до якого прикладені: сила
тяжіння
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 63
75 |
Для чого проводиться силовий аналіз механізмів? |
1 |
Для визначення положень, переміщень, траєкторій, швидкостей та прискорень точок і ланок. |
2 |
Для поділу механізму на структурні групи та визначення класу механізму. |
3 |
для визначення реакцій в кінематичних парах і зрівноважуючого моменту, необхідних для розрахунків на міцність, жорсткість, вібростійкість, зношування, довговічність та інших. |
4 |
Для визначення кінематичних параметрів механізму. |
Питання 64
75 |
У якій послідовності проводиться силовий аналіз механізмів? |
1 |
розглядається механізм І класу, перша приєднана структурна група, друга і т.д. до останньої. |
2 |
розглядається перша приєднана структурна група, друга і т.д. до останньої. |
3 |
визначаються реакції першої приєднаної структурної групи, другої і т.д. до останньої. |
4 |
розглядається остання приєднана структурна група, тоді передостання і т.д. до механізму І класу. |
Питання 65
75 |
За якою формулою
визначається зведений до кривошипа
момент сил?
У формулах
-
кутова швидкість кривошипа;
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 66
50 |
Як спрямувати силу тертя? |
1 |
Проти напряму прискорення. |
2 |
Проти напряму відносної швидкості. |
3 |
Вздовж нормалі до поверхні. |
4 |
Вздовж напрямку прискорення. |
Питання 67
50 |
У яких одиницях вимірюється коефіцієнт тертя ковзання? |
1 |
Безрозмірна величина. |
2 |
В метрах. |
3 |
В градусах. |
4 |
В радіанах. |
Питання 68
100 |
Якою
тригонометричною функцією від кута
тертя
|
1 |
Косинус кута . |
2 |
Синус кута . |
3 |
Тангенс кута . |
4 |
Котангенс кута . |
Питання 69
75 |
В яку сторону по відношенню до напрямку руху відхиляється вектор повної реакції неідеальної шорсткої поверхні? |
1 |
Назад на кут тертя від нормалі до поверхні. |
2 |
Вперед на кут тертя від нормалі. |
3 |
Не відхиляється від нормалі. |
4 |
По дотичній вперед. |
Питання 70
50 |
Сила тертя ковзання дорівнює добутку сили нормального тиску на яку величину? |
1 |
На коефіцієнт тертя ковзання. |
2 |
На синус кута тертя. |
3 |
На косинус кута тертя. |
4 |
На котангенс кута тертя. |
Питання 71
100 |
В яких одиницях вимірюється коефіцієнт тертя кочення? |
1 |
Безрозмірна величина. |
2 |
В лінійних одиницях, метрах. |
3 |
В градусах. |
4 |
В радіанах. |
Питання 72
75 |
За якою формулою
визначається зведений до кривошипа
момент інерції?
У формулах
-
кутова швидкість кривошипа;
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 73
75 |
За якою формулою визначається кінетична енергія шатунів, коромисел і куліс? У формулах , – маса та кутова швидкість –тої ланки; – швидкість центра мас –тої ланки; –момент інерції –тої ланки відносно її центра мас. |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 74
100 |
Який вигляд
має рівняння руху машинного агрегату
в диференціальній формі?
У формулах
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 75
50 |
Чому дорівнює
кінетична енергія
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 76
75 |
Навести формули
для визначення коефіцієнта нерівномірності
руху. Тут
|
1 |
|
2 |
|
3 |
|
4 |
|
Модуль 5. синтез механізмів
Питання 77
75 |
Кулачком називається: |
1 |
ланка, яка рухається зворотно–поступально. |
2 |
ланка, якій належить елемент вищої кінематичної пари у вигляді поверхні змінної кривизни. |
3 |
ланка, яка рухається обертально. |
4 |
ланка, якій належить елемент нижчої кінематичної пари. |
Питання 78
75 |
Яке значення приймає коефіцієнт висоти головки зуба: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 79
75 |
Яке значення приймає коефіцієнт висоти ніжки зуба: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 80
75 |
Яке значення приймає коефіцієнт радіального зазора: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 81
75 |
Яке значення приймає коефіцієнт закруглення зуба: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 82
75 |
Навести
формули для визначення коефіцієнтів
питомого ковзання
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 83
75 |
Значення коефіцієнта перекриття показує: |
1 |
кількість пар зубів, які знаходяться в зачепленні. |
2 |
середню кількість пар зубів, які знаходяться в зачепленні одночасно. |
3 |
кількість пар зубів, які входять в зачеплення. |
4 |
середню кількість зубів, які знаходяться в зачепленні. |
Питання 84
75 |
формули для визначення радіусів кіл западин циліндричного евольвентного зубчастого зачеплення: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 85
75 |
Навести рівняння
евольвенти в параметричній формі. Тут
– кут профілю, який визначає положення
точки на евольвенті;
–
евольвентний кут або інволюта; ρ
– довжина радіус-вектора
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 86
75 |
Активною лінією зачеплення називається: |
1 |
відрізок, дотичний до основних кіл, який міститься між точками дотику. |
2 |
відрізок між точками перетину теоретичної лінії зачеплення з колами вершин зубів. |
3 |
відрізок між точками перетину кіл вершин зубів. |
4 |
відрізок, перпендикулярний до кіл западин зубів. |
Питання 87
75 |
формули для визначення радіусів основних кіл циліндричного евольвентного зубчастого зачеплення: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 88
75 |
формули для визначення радіусів ділильних кіл циліндричного евольвентного зубчастого зачеплення: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 89
75 |
формули для визначення радіусів кіл вершин циліндричного евольвентного зубчастого зачеплення: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 90
50 |
Як визначається міжосьова відстань циліндричного евольвентного зубчастого зачеплення? |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 91
75 |
формули для визначення радіусів початкових кіл циліндричного евольвентного зубчастого зачеплення: |
1 |
|
2 |
|
3 |
|
4 |
|
Питання 92
100 |
Як коефіцієнт
перекриття циліндричного евольвентного
зачеплення залежить від модуля, кута
зачеплення
|
1 |
коефіцієнт перекриття збільшується з ростом модуля, кута зачеплення та передаточного відношення. |
2 |
коефіцієнт перекриття не залежить від модуля, зменшується з ростом кута зачеплення і збільшується зі збільшенням передаточного відношення. |
3 |
коефіцієнт перекриття не залежить від модуля, зменшується з ростом кута зачеплення і передаточного відношення. |
4 |
коефіцієнт перекриття не залежить від модуля, збільшується з ростом кута зачеплення і передаточного відношення. |
Питання 93
50 |
Навести умову співвісності для показаної схеми планетарного механізму.
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 94
50 |
Навести умову співвісності для показаної схеми планетарного механізму.
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 95
100 |
Навести умови сусідства для показаної схеми планетарного механізму.
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Питання 96
100 |
Навести умову складання для показаної схеми планетарного механізму.
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Питання 97
100 |
Навести умови сусідства для показаної схеми планетарного механізму.
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Питання 98
75 |
Навести умову складання для показаної схеми планетарного механізму.
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 99
75 |
Якими є умова відсутності підрізання та заклинювання зубів для показаної схеми планетарного механізму.
|
1 |
|
2 |
|
3 |
|
4 |
|
Питання 100
75 |
Якими є умова відсутності підрізання та заклинювання зубів для показаної схеми планетарного механізму.
|
1 |
|
2 |
|
3 |
|
4 |
|

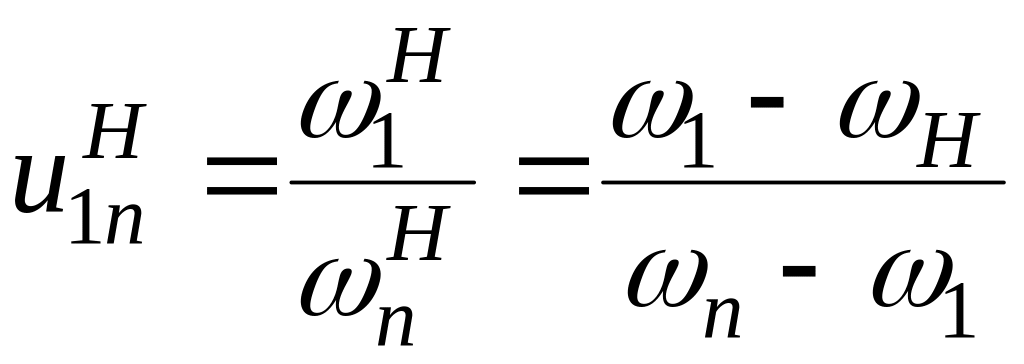 .
.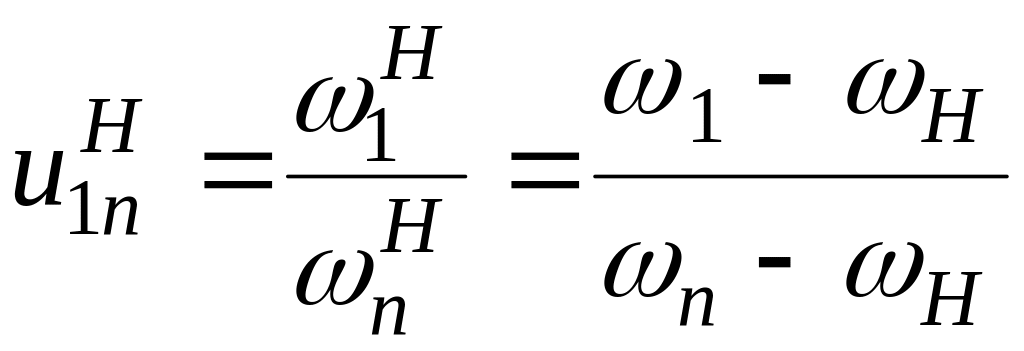 .
.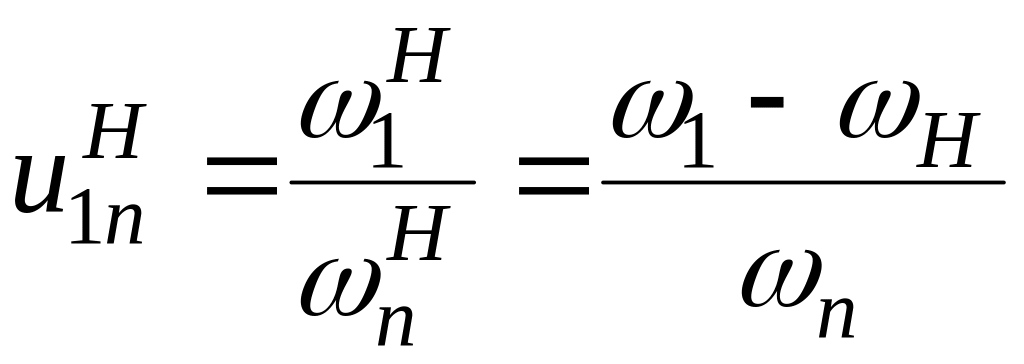 .
.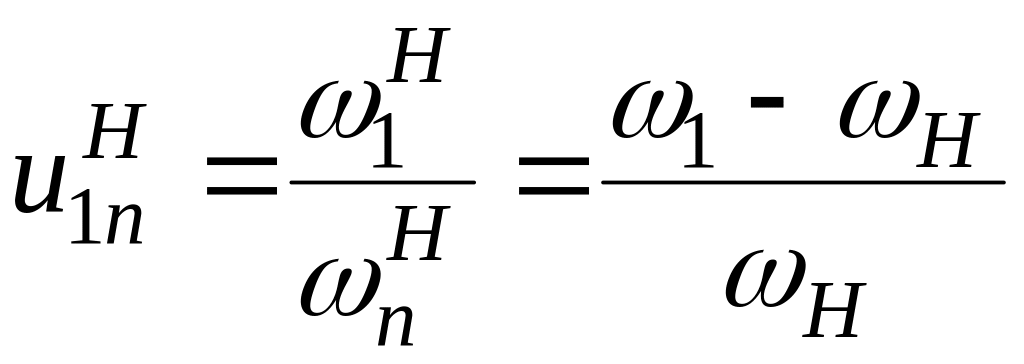 .
.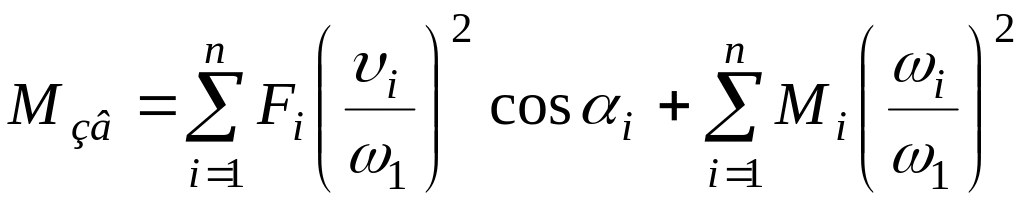 .
.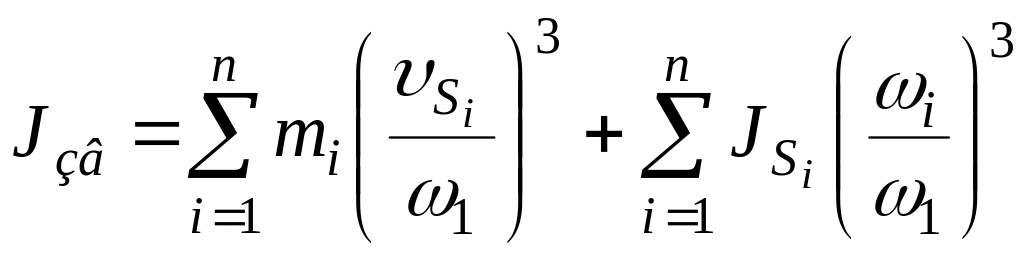 .
. .
.