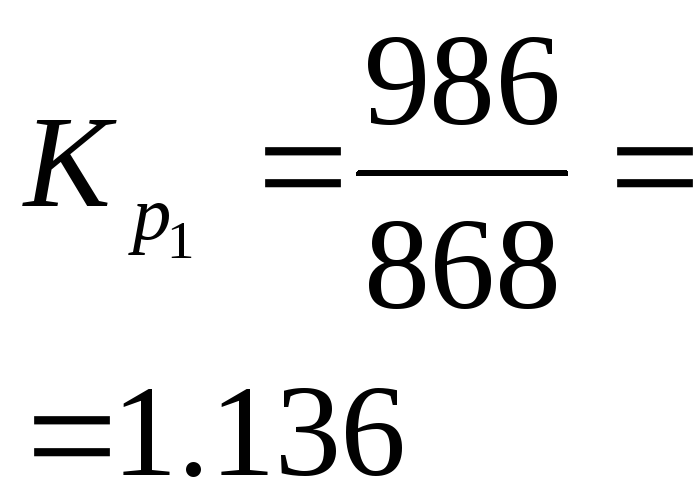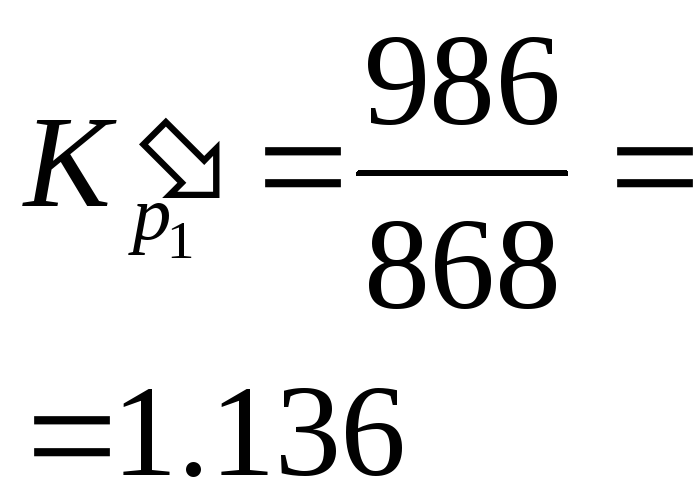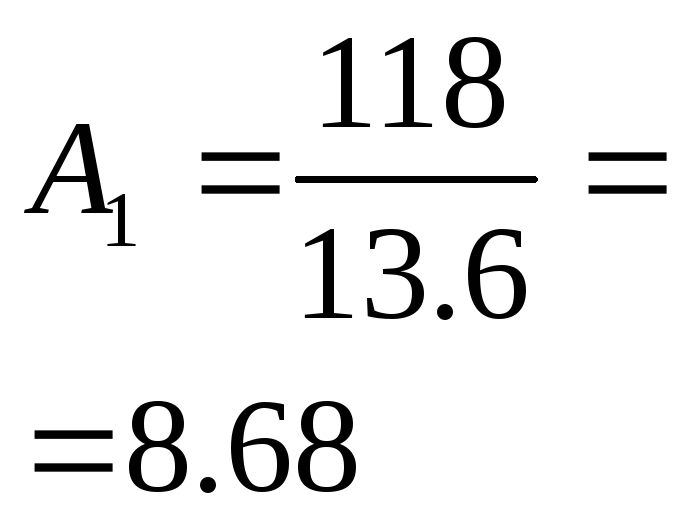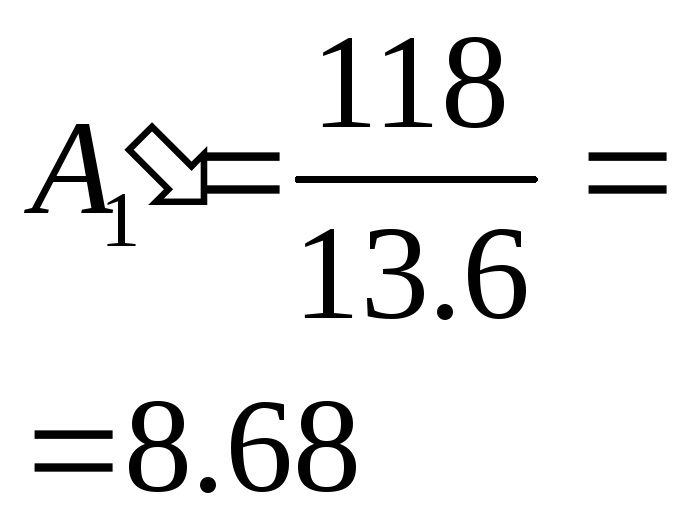Расчет внутригрупповой дисперсии по второй группе(число грузчиков -4)

Время простоя под разгрузкой (мин.т.),х	Число выполненных разгрузок,			()
8 10 12	3 2 1	24 20 12	-1.33 0.67 2.67	5.31 0.90 7.13
Итого	6	56	-	13.37

Средняя из внутригрупповых дисперсий:

Межгрупповая дисперсия, отражающая различия в величине признака под влиянием фактора, положенного в основу группировки, определяется по формуле:

Общая дисперсия () равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии: =4.3+10.7=15.0, что и соответствует полученной ранее величине.

Задача 4. Имеются следующие данные о результатах обследования рабочих предприятия по размеру месячной заработной платы. (табл.1)

Таблица 1

Группы рабочих по возрасту, лет	Число рабочих	Дисперсия заработной платы
До 20	100	300
20-30	120	400
30 и старше	150	500

Общая дисперсия в обследованной совокупности рабочих составила 450.Определить, в какой степени вариация заработной платы рабочих предприятия зависит от возраста.

Решение

Средняя внутригрупповая дисперсия характеризует случайную вариацию под влиянием неучтенных факторов:

Межгрупповая дисперсия отражает систематическую вариацию под влиянием фактора, положенного в группировки (возраста рабочих). Межгрупповая дисперсия определяется по правилу сложения дисперсий: =-=450-413.5=36.5. Отсюда соотношение дисперсий: :=36.5:450=0.08, или 8.0%. Поэтому возраст на варьирование заработной платы рабочих предприятия не оказывает существенного влияния.

Статистическое изучение динамики

Задача 1. Имеются следующие данные о выпуске легковых автомобилей в России (табл. 1). Рассчитайте показатели динамики выпуска легковых автомобилей от года к году и средние за весь анализируемый период

Таблица 1

Год	1996	1997	1998	1999
Произведено легковых автомобилей, тыс шт.	868	986	840	956

Решение

Расчет показателей динамики от года к году представлен в табл.2

Таблица 2

Расчет показателей динамики от года к году

показатель		Год
		1996	1997	1998	1999
Абсолютный прирост,,тыс шт.	С переменной базой	-	=986-868=118
	С постоянной базой	-	=986-868=118
Коэффициент роста (К)	С переменной базой	-
	С постоянной базой	-
Темп роста (Т). %	С переменной базой	-
	С постоянной базой	-
Темп прироста Т,%	С переменной базой	-
	С постоянной базой	-
Абсолютное значение 1% прироста А, тыс шт.	С переменной базой	-
	С постоянной базой	-

Средний уровень интервального ряда динамики:

Средний абсолютный прирост:

Средний коэффициент роста:

Средний темп роста:

Средний темп прироста:

Средняя величина абсолютного значения 1% прироста:

Задача 2. Имеются следующие данные о стоимости имущества предприятия (млн руб) (табл.1). Определить абсолютное и относительное изменение среднегодовой стоимости имущества предприятия в 2000 г. по сравнению с 1998 и 1999 гг.

Таблица 1

год	Отчетные данные
	1.01	1.04	1.07	1.10
1998 1999 2000 2001	62 68 80 95	65 70 84 -	70 75 88 -	68 78 90 -

Решение

Поскольку промежутки времени между датами равны, средний уровень моментного ряда динамики исчисляется по формуле

,где y₁ и y_n-уровни соответственно на начало и на конец периода за который исчисляется средний уровень; n- число уровней ряда.

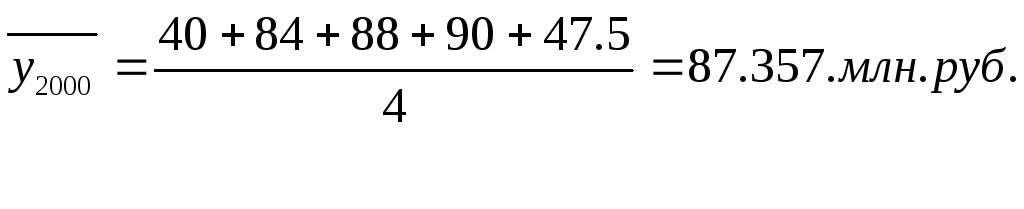
В 2000 г. среднегодовая стоимость имущества предприятия возросла по сравнению с 1998 г. на 20.375 млн., или на 3.04 %, и по сравнению с 1999 – на 13.125 млн. руб., или на 17.7 %.

Задача 3.Количество дорожно-транспортных происшествий, совершенных водителями в регионе увеличилось в 1995 г. по сравнению с 1990г. на 2 тыс., или на 4%; в 1997 г. по сравнению с 1995г. их число возросло на 30%, а в 2000 г. по сравнению с 1997 г. их число возросло на 2%. Определите количество ДТП в 1990, 1995. 1997, 2000 гг.

Решение

Уровень ДТП в 1990 г. определяется по формуле: ,

где абсолютная величина 1% прироста для 1995 г.;

Далее, недостающие уровни 1995, 1997, 2000 гг. определим, зная темпы роста для соответствующего периода, тыс. ед.: