
-
Лекция №4 26.02.09
Зав. Кафедры 402 профессор Мазепа Роман Богданович
Системы и сети связи.
(Телекоммуникационные системы и сети).
Процедура цифрового представления включает два процесса:
Временная дискретизация
В простейшем случае осуществляется через постоянный интервал, выбираемый исходя из теоремы Котельникова (не по теореме, а исходя из соображений)
Квантование по уровню
Возникают две ошибки:
При ограничении спектра
При усечении ряда Котельникова
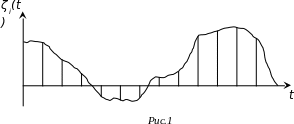
В результате временной дискретизации остаются дискретные по времени значения:
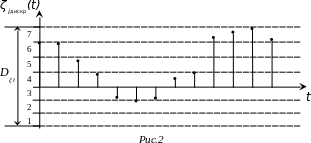
Закончена процедура временной дискретизации.
Но каждое из этих значений, в силу того, что это непрерывная, случайная функция времени, может принимать одно из безконечного множества значений, т.е. мы избавились от одной из двух безконечностей: от безконечного числа значений первичного сигнала на ограниченном интервале времени.
Путём квантования мы избавляемся от второй безконечности.
Берём Dζ i (динамический диапазон первичного сигнала) и делим на определённое количество зон квантования.
Что получаем в результате квантования?
В процессе квантования каждое дискретное по времени значение заменяется номером зоны квантования, в которое это значение попадает.
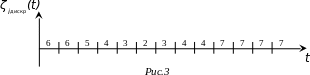
Данная последовательность цифр есть цифровое представление первичного сигнала.
Она может быть представлена с помощью любого другого алфавита, например двоичного:
010 = 0002 410 = 1002
110 = 0012 510 = 1012
210 = 0102 610 = 1102
310 = 0112 710 = 1112
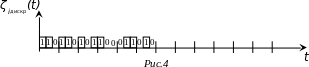
Воспроизведение.
На каждом интервале будет восстановлен уровень, соответствующий середине зоны квантования.
Воспроизводящее устройство знает шаг квантования и, получая номер, оно строит на интервале вместо реального процесса «ступеньку» и т.д.
Вместо реального процесса воспроизведётся ступенчатый процесс:
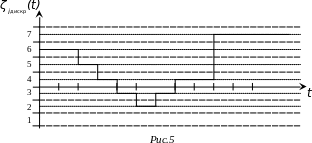
Можно оценить ошибку, которая при этом получается.
Когда мы заменяем значение номером зоны квантования, то это значение может быть меньше половины зоны квантования, а может быть больше, значит наибольшая ошибка, которая возникает при восстановлении, будет не больше половины зоны квантования. Значение ошибки будет случайным, но если шаг квантования достаточно маленький, то мы можем считать, что случайная ошибка распределена равновероятно, т.е. плотность вероятности ошибки Wx (Z) при малом шаге квантования будет равновероятной в пределах ±Δ/2.
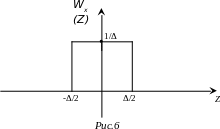
Можно вычислить мощность ошибки.
Шаг квантования можно выбирать, исходя из среднеквадратического значения ошибки, вычислив дисперсию ошибки.
При данном распределении математическое ожидание ошибки будет равно нулю – тогда мощность ошибки будет равна дисперсии:
(1)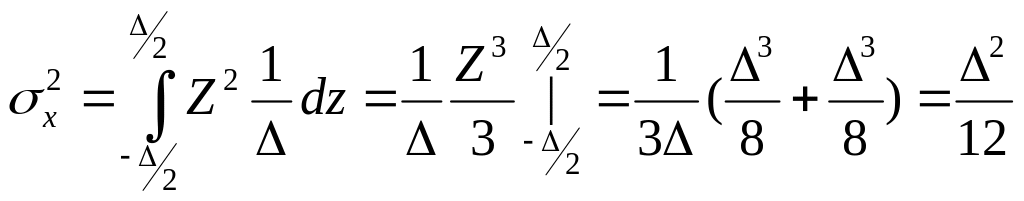
Теперь, если имеем мощность ошибки, можно вычислить относительную среднеквадратическую ошибку:
(2)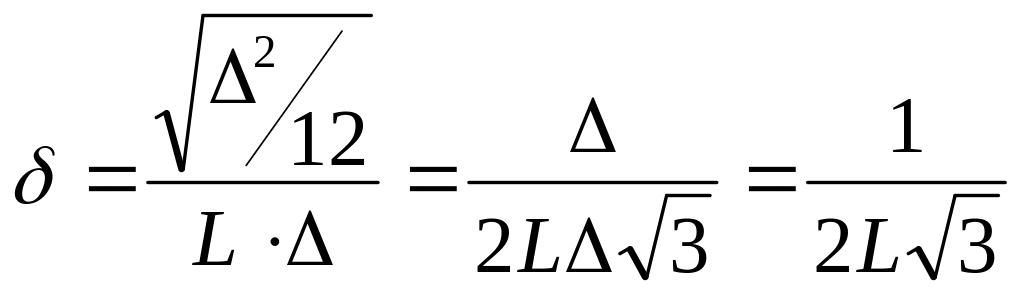
![]() -
динамический диапазон
-
динамический диапазон
Пример
Число уровней квантования для значения 0.01.
(3)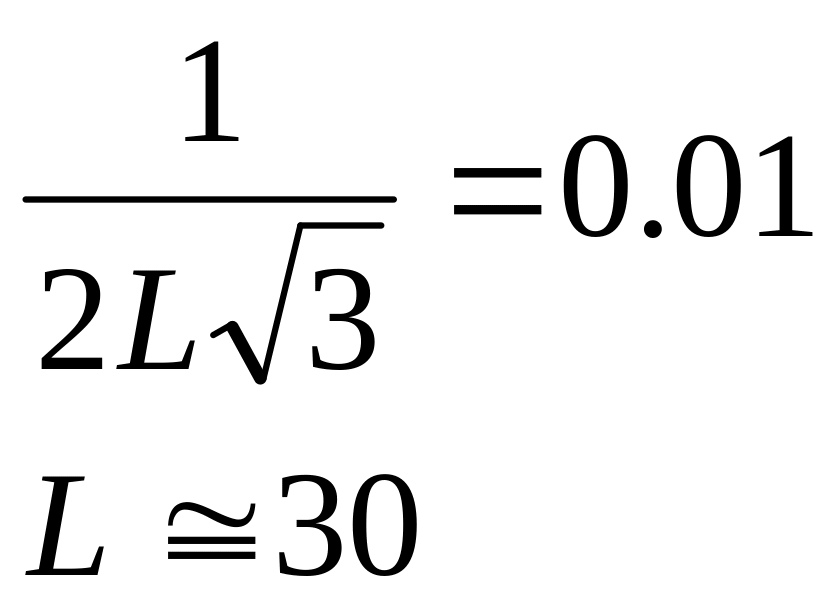
для такого количества уровней квантования необходимо 5 разрядов (25 = 32).
Количество разрядов определяется требуемой точностью.
Чем точнее потребитель потребует представление первичного сигнала, чем меньше будет ошибка квантования, тем больше потребуется разрядность кодового слова.
Можно вычислить, исходя из максимальной ошибки:
(4)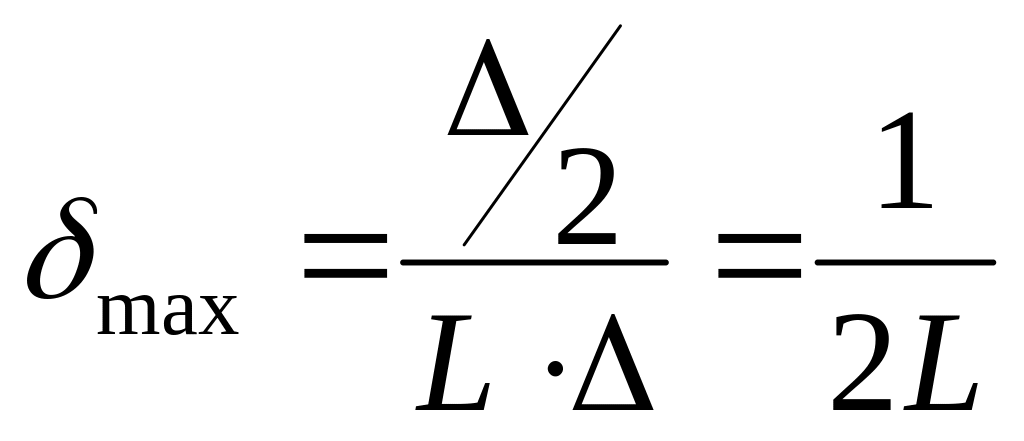
Тогда для 0.01 понадобится 50 зон квантования и количество разрядов 6 (26 = 64).
Устройство, которое осуществляет представление первичного сигнала в цифровой форме, называют кодером источника (КИ).
Простейшее цифровое представление обладает следующим существенным недостатком: состояние источника физической системы во времени меняется, причём, как говорят, по нестационарному закону. Система либо развивается, либо деградирует – это значит, что процесс изменения состояния нестационарный. А если процесс состояния системы нестационарный, то изменение параметров также представляет собой нестационарный случайный процесс. А если случайный процесс нестационарный, это обозначает, что статистические характеристики процесса во времени меняются, а значит, во времени меняется спектр (спектр "дышит").
Исходя из какой формы спектра, выбирать максимальную частоту при таком простейшем цифровом представлении?
Чтобы гарантировать точность, мы должны исходить из наихудшего спектра – из максимальной ширины спектра, т.е. это такая ширина спектра, вероятность появления которой в жизни достаточно маленькая (вероятность которой не более 10-7). Исходя из этой ширины спектра, выбираем wmax. И из wmax выбираем интервал дискретизации. Получится, что основное время работы системы будут передаваться ненужные для потребителя сведения и только в какой-то очень маленький промежуток времени работы системы, когда ширина спектра достигает наибольшего значения, мы будем передавать именно то, что ?? 0ч32м04с ?? сам потребитель.
В этом основной недостаток этого простейшего цифрового представления первичного сигнала.
Цифровое представление первичного сигнала позволяет частично избавиться от одной из двух избыточностей первичного сигнала (в первичном сигнале могут быть два вида избыточности: статистическая и семантическая).
Статистическая: часть значений первичного сигнала является ненужной, лишней для потребителя. Всегда в первичном сигнале содержится статистическая избыточность, причины которой в том, что:
1 – значения первичного сигнала в силу инерционности источника статистически зависимы друг от друга,
2 – эти значения неравновероятны.
в силу этих причин часть сведений, которые содержатся в этих значениях, являются излишними, повторяются от одного значения к другому.
Семантическая избыточность – причина в том, что полезными для целенаправленных действий являются не все значения первичного сигнала, или же даже не сами значения первичного сигнала, а какие-то характеристики.
Сущность этого уменьшения состоит в том, что наши органы восприятия обладают ограниченной разрешающей способностью, это значит, что очень близкорасположенные значения первичного сигнала мы не различаем, а если мы их не различаем и не можем использовать, то безсмысленно их передавать потребителю. Дискретизация по времени избавляет от значительного числа дискретных значений, которые с точки зрения требуемой потребителю точности не нужны, а квантование по уровню также уменьшает количество значений, потому что возможных значений по уровню безконечно велико, а мы их представляем ограниченным числом

Преимущества цифрового представления первичного сигнала:
Для преобразования представленных в цифровой форме сигналов можно использовать дискретные элементы (хороши тем, что они более устойчивы к воздействию внешних факторов, дешевле)
Позволяет сопротивляться воздействию помех при передаче первичных сигналов, хранении
Схема телекоммуникационной системы
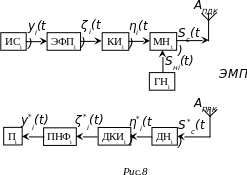
При передаче радиосигнала Si(t) в каком-то из вариантов ЭМП на сигнал действуют различные шумы и помехи. Воздействие шумов и помех на радиосигнал приводит к возникновению дополнительных ошибок в передаче первичного сигнала: одни ошибки возникли в результате цифрового представления, – помехи добавляют ошибки, в том виде, что в демодуляторе несущего сигнала (ДН) часть символов передаётся с искажением ("0"→ "1", "1"→ "0"). Ошибка в уровне (зоне) квантования – не правильно воспроизведённый на этом интервале первичный сигнал.
Необходимо с этим явлением бороться. Надо таким образом строить радиосигнал с помощью модулятора и таким образом строить демодулятор, чтобы вероятность таких изменений (трансформаций символов/кодовых слов) была приемлемо маленькой.
Построение оптимальной с точки зрения помехоустойчивости телекоммуникационной системы.
Цифровое представление любого сигнала, в том числе первичного сигнала, можно передавать двумя основными способами:
