ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Орловский государственный технический Университет

Д.Н. Ешуткин и др.

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНЫХ РАБОТ

Задание Д-3. Принцип Даламбера

Рекомендовано редакционно-издательским советом ОрелГТУ

в качестве учебного пособия

Орел 2006

УДК Е 96 531 (076)

ББК 22.21 7

Е 96

Рецензенты:

кандидат технических наук, заведующий кафедрой общеинженерных дисциплин Орловского государственного аграрного университета

Г.М. Абрамов,

кандидат технических наук, доцент кафедры «Динамика и прочность машин»

А.Ю. Корнеев

Е 96 Ешуткин, Д.Н. Теоретическая механика, задания для самостоятельных работ: учебное пособие/ Д.Н. Ешуткин, А.И. Пономарев, Е.Н. Грядунова, А.В. Журавлева. — Орел: ОрелГТУ, 2006. — 122 с.

Учебное пособие содержит задания для самостоятельных работ, которые охватывают все основные разделы теоретической механики: статику, кинематику и динамику, и задачи по всем главным темам этих разделов. К каждому заданию дается подробное указание по выполнению, формулы и примеры.

Учебное пособие отвечает содержанию рабочих программ по теоретической механике и предназначено студентам, обучающимся на всех специальностях очной и заочной форм обучения, изучающих дисциплину «Теоретическая механика».

УДК 531 (076)

ББК 22.21 7

Е 96

© ОрелГТУ, 2006

ВВЕДЕНИЕ

Теоретическая механика – это наука о законах механического движения и равновесия материальных тел. Под механическим движением понимается изменение относительного положения материальных тел в пространстве с течением времени. Теоретическая механика изучает наиболее общие законы механического движения. Она не учитывает индивидуальные свойства материальных тел, за исключением двух свойств: протяженности и гравитации. Наблюдать и изучать механическое движение материальных тел можно по отношению к другим материальным телам, принятым за тела отсчета. С этими телами обычно связывают систему координатных осей, которую называют системой отсчета. Частным случаем механического движения является равновесие материальных тел.

Теоретическую механику условно делят на статику, кинематику и динамику.

В данном пособии приведены достаточно простые задачи по основным разделам теоретической механики, решение которых позволяет освоить основные алгоритмы применения теоретических положений на практике.

Характерная особенность приведенных заданий – несложность использования математических выкладок и их физическая прозрачность, что позволяет не акцентировать внимание студента на конкретных условиях задачи, а понять при самостоятельной работе алгоритм решения подобного класса задач.

3 ДИНАМИКА

Динамикой называется раздел теоретической механики, в котором изучается движение материальных тел (точек) с учетом действующих на них сил.

3.3 Задание Д-3. Принцип Даламбера

3.3.1 Определение реакции осей вращающихся тел

Используя условия задания Д-2 (рис. 3.32 - 3.61, табл. 9) определить реакции осей вращающихся тел 1 и 2 (для ) с помощью принципа Даламбера. В вариантах, где имеется соприкосновение колес 1 и 2, дополнительно найти усилие в точке их касания.

Принцип Даламбера заключается в том, что в любой момент времени активные силы, приложенные к точкам рассматриваемой механической системы, реакции связей и силы инерции точек механической системы образуют уравновешенную систему сил. Сила инерции материальной точки (знак «минус» показывает, что направлены противоположно). Для твердого тела определяются главный вектор и главный момент сил инерции Известно, что если твердое тело совершает поступательное движение, то силы инерции имеют равнодействующую, приложенную в центре масс тела. Силы инерции тела, вращающегося вокруг неподвижной оси, проходящей через центр масс, имеют главный вектор равный нулю, так как , поэтому силы инерции приводятся к паре сил, момент которой относительно оси вращения (z):

.

знак «минус» показывает, что и имеют противоположные направления.

3.2.2 Указания по выполнению задания Д-3

При выполнении этого задания рекомендуется придерживаться следующего порядка:

1. Выбрать механическую систему.

2. Приложить к выбранной системе активные внешние силы и внешние реакции связей.

3. Приложить силы инерции точек, главные векторы и главные моменты сил инерции тел.

4. Составить условия равновесия системы сил (активных реакций связей и сил инерции в соответствии с типом системы сил).

Если в этих условиях присутствуют неизвестные, они образуют систему уравнений, решая которые, необходимо определить искомые величины. Отсюда следует, что число определяемых неизвестных не может быть больше числа неизвестных.

3.3.3 Примеры выполнения задания Д-3

П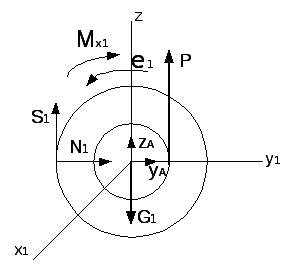ример Д-3.1. Воспользуемся условием примера Д-2.1 (рис. 3.62). В данном случае, рассматриваемую механическую систему разделим на две части: I – колесо 1; и II – колесо 2 и груз 3. Применим к колесу 1 принцип Даламбера: приложим к нему все активные силы, реакции связей и силы инерции и получим уравновешенную систему сил. Силы инерции вращающегося тела в данном случае приводятся к паре сил, момент которой .

Знак «минус» показывает, что и имеют противоположные направления. Составим условия равновесия плоской системы по рис. 3.63.

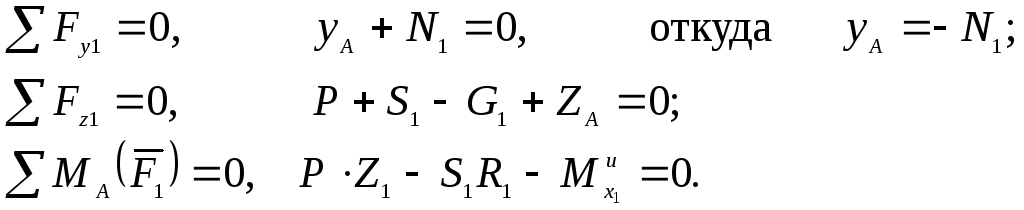
Учитывая, что , получим:

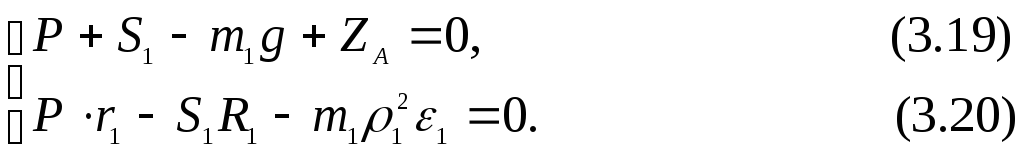
Полученная система не может быть решена однозначно, так как число неизвестных () превышает число уравнений.

Рассмотрим часть II механической системы, к которой также применим принцип Даламбера (рис. 3.64). Здесь – сила инерции поступательно движущегося тела: .

Составим уравнения равновесия:

(3.21)

(3.22)

Учитывая, что , а также , после преобразования уравнений (3.19) - (3.22) получим систему 4-х уравнений с четырьмя неизвестными:

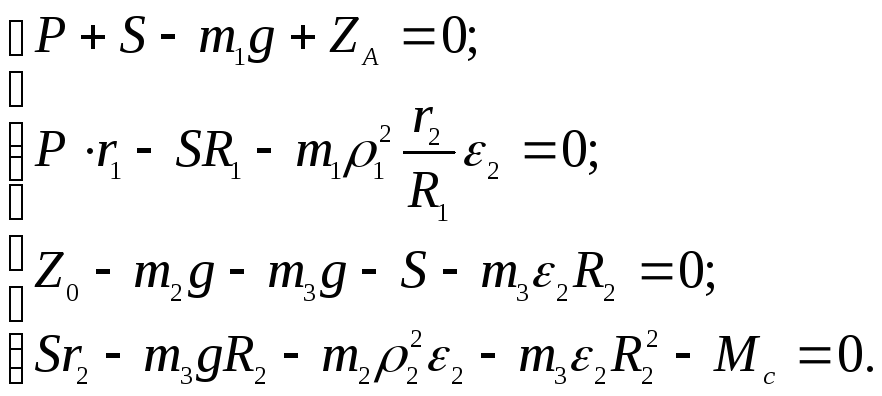(3.23)

Из второго уравнения данной системы выразим S:

(3.24)

и подставим в четвертое уравнение той же системы.

Тогда

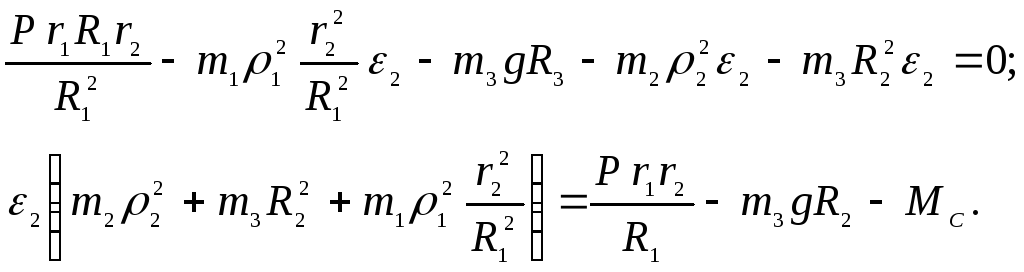
Умножим обе части на R₁:

;

(3.25)

Подставляя (3.25) в (3.24), получим:

. (3.25)

Теперь, подставляя (3.25) в первое уравнение системы (3.23), будем иметь:

. (3.26)

И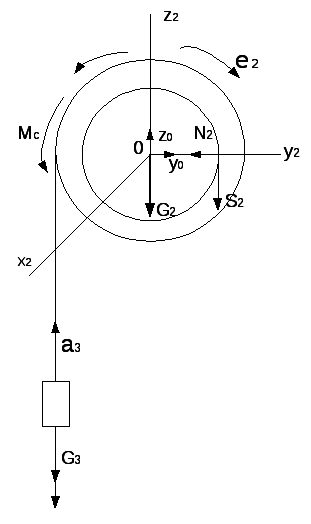 з третьего уравнения системы (3.23) найдем

. (3.27)

Подставляя значения заданных величин в (3.25) - (3.27) и имея t = 3с, найдем: .

Ответ:

Примечания:

1. Этот метод можно применить и для решения примера Д-2.1, так как .

2. Величины и зависят от особенностей конструкции конкретных механизмов, поэтому не могут быть определены в рамках данного принципа.

Приложения А

Образец оформления титульного Титульный листа

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Орловский государственный технический Университет

Кафедра - "Теоретическая и прикладная механика"

Расчетно-графическая работа

по дисциплине "Теоретическая механика"

Название работы

Работу выполнил студент

Группа

Специальность

Вариант

Руководитель

Орел, 200 г.

Литература

1. Тарг, С.М. Краткий курс теоретической механики/ С.М. Тарг. - М.: Наука, 1972. – 478 с.

2. Яблонский, А.А. Курс теоретической механики. Часть 1, 2/ А.А. Яблонский, В.М. Никифорова. - М.: Высш. школа, 1984. – 343 с.

3. Добронравов, В.В. Курс теоретической механики/ В.В. Добронравов, Н.Н. Никитин, А.Л. Дворников. - М.: Высш. школа 1983. – 575 с.

4. Воронков, И.М. Курс теоретической механики/ И.М. Воронков. - М.: Наука, 1966. – 596 с.

5. Савин, Г.Н. Курс теоретической механики/ Г.Н. Савин, Т.В. Путята, Б.Н. Фрадлин. - Киев: Высш. школа, 1973. – 359 с.

6. Лойцянский, Л.Г. Курс теоретической механики. Т.1./ Л.Г. Лойцянский, А.И. Лурье. - М.: Наука, 1982. – 352 с.

7. Бать, М.И. Теоретическая механика в примерах и задачах. Часть 1./ М.И. Бать, Г.Ю. Джанелидзе, А.С. Кельзон. - М.: Наука, 1984. – 503 с.

8. Ешуткин, Д.Н. Сборник задач по теоретической механике/ Д.Н. Ешуткин, А.И. Пономарев, Е.Н. Грядунова. – Орел: ОрелГТУ, 2005. – 88с.