Обобщенные модели взаимодействия двух видов

Было предложено большое число моделей, описывающих взаимодействие видов, правые части уравнений которых представляли собой функции численностей взаимодействующих популяций. Решался вопрос о выработке общих критериев, позволяющих установить, какого вида функции могут описать особенности поведения временного численности популяции, в том числе устойчивые колебания. Наиболее известные из этих моделей принадлежат Колмогорову (1935, переработанная статья ‑ 1972) и Розенцвейгу (1963).

А.Н.Колмогоров рассмотрел обобщенную модель взаимодействия биологических видов типа хищни‑жертва или паразит‑хозяин. Модель представляет собой систему двух уравнений общего вида

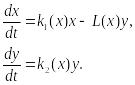(9.12)

В модель заложены следующие предположения:

1) Хищники не взаимодействуют друг с другом, т.е. коэффициент размножения хищников k₂ и число жертв L, истребляемых в единицу времени одним хищником, не зависит от y.

2) Прирост числа жертв при наличии хищников равен приросту в отсутствие хищников минус число жертв, истребляемых хищниками. Функции k₁(x), k₂ (x), L(x), ‑ непрерывны и определены на положительной полуоси x, y ³0.

3) dk₁/dx<0. Это означает, что коэффициент размножения жертв в отсутствие хищника монотонно убывает с возрастанием численности жертв, что отражает ограниченность пищевых и иных ресурсов.

4) dk₂ / dx>0, k₂ (0) < 0 < k₂ (¥). С ростом численности жертв коэффициент размножения хищников монотонно убывает с возрастанием численности жертв, переходя от отрицательных значений, (когда нечего есть) к положительным.

5) Число жертв, истребляемых одним хищником в единицу времени L(x)>0 при N>0; L(0)=0.

Возможные типы фазовых портретов системы (9.12) представлены на рис. 9.6:

 

 

 

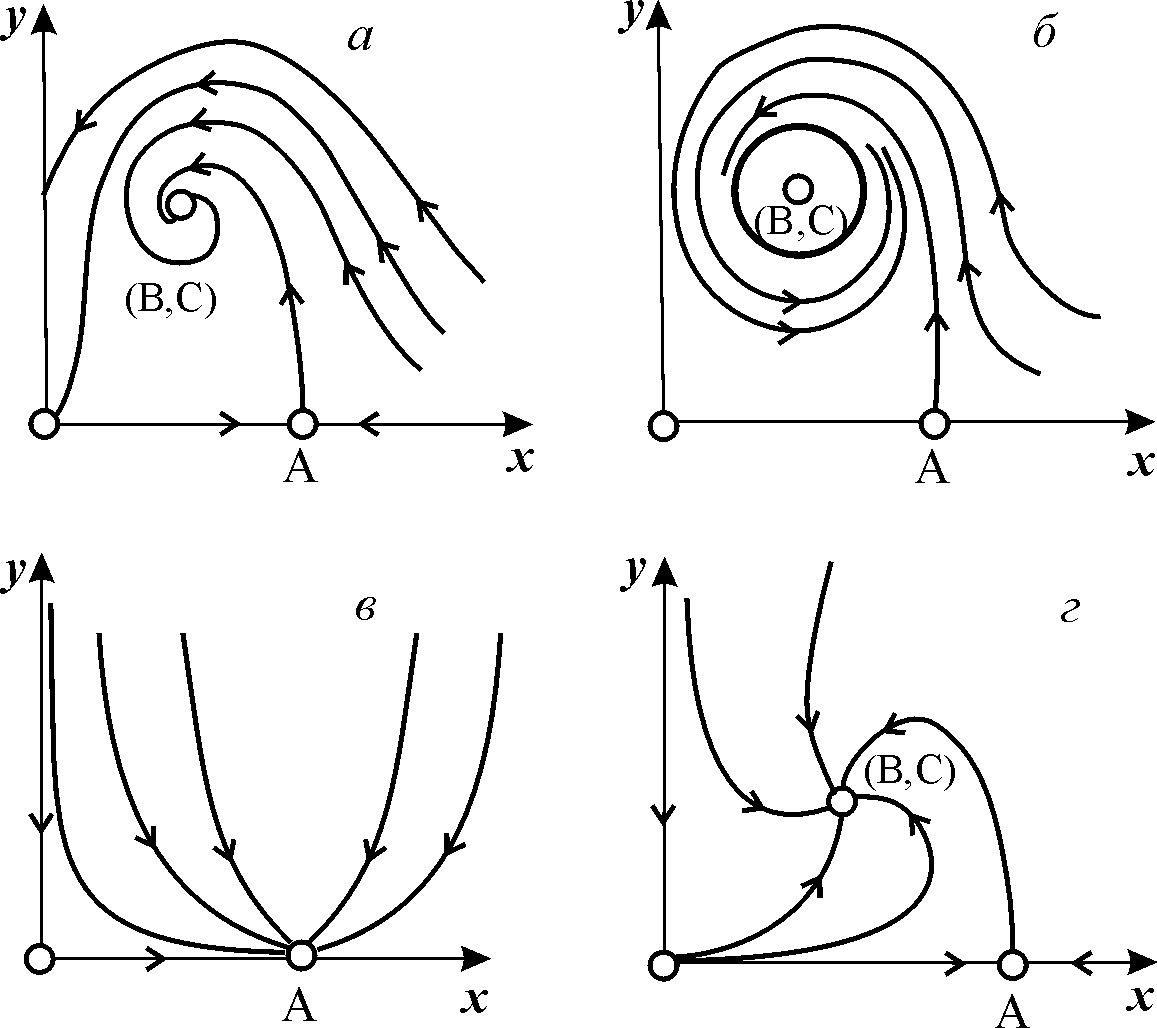
Рис. 9.6. Фазовые портреты системы Колмогорова (9.12), описывающей взаимодействие двух видов при разных соотношениях параметров. Пояснения в тексте.

 

 

Стационарные решения (их два или три) имеют следующие координаты:

(1). `x=0; `y=0.

Начало координат при любых значениях параметров представляет собой седло (рис. 9.6 а-г).

(2). `x=A,`y=0. (9.13)

A определяется из уравнения:

k₁ (A)=0.

Стационарное решение (9.13) ‑ седло, если B<A (рис. 9.6 а, б, г), B определяется из уравнения

k₂(B)=0

Точка (9.13) помещается в положительном квадранте, если B>A. Это ‑ устойчивый узел.

Последний случай, который соответствует гибели хищника и выживанию жертвы, представлен на рис. 9.6 в.

(3). `x=B,`y=C. (9.14)

Величина С определяется из уравнений:

Точка (9.14) – фокус (рис.9.6 а) или узел (рис.9.6 г), устойчивость которых зависит от знака величины s

s²= – k₁ (B) – k₁ (B)B+L(B)C.

Если s>0, точка устойчива, если s<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 б)

 

В зарубежной литературе чаще рассматривается сходная модель, предложенная Розенцвейгом и Макартуром (1963):

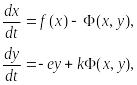(9.15)

где f(x) - скорость изменения численности жертв x в отсутствие хищников, Ф(x,y) ‑ интенсивность хищничества, k ‑ коэффициент, характеризующий эффективность переработки биомассы жертвы в биомассу хищника, e - смертность хищника.

Модель (9.15) сводится к частному случаю модели Колмогорова (9.12) при следующих предположениях:

1) численность хищника ограничивается только численностью жертвы,

2) скорость, с которой данная особь хищника поедает жертву, зависит только от плотности популяции жертв и не зависит от плотности популяции хищников.

Тогда уравнения (9.15) принимают вид.

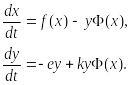
При описании взаимодействия реальных видов, правые части уравнений конкретизируются в соответствии с представлениями о биологических реалиях. Рассмотрим одну из самых популярных моделей такого типа.