Задача управления

Если речь идет об управлении организационными системами, давайте поймем сначала, что такое управление. Формальное определение таково: управление – воздействие на управляемую систему с целью обеспечения требуемого ее поведения. Значит надо детализировать, что такое «управляемая система», что такое «воздействие», что такое «поведение», с чьей точки зрения «требуемым» оно должно быть и т.д.

Рассмотрим простейшую входо-выходную модель системы, состоящей из управляющего органа – центра – и управляемого субъекта¹ – агента – см. рисунок 3. Имеются: на входе – управляющее воздействие и внешние воздействия, на выходе – действие управляемого субъекта. Добавляем обратную связь (управляющий орган знает состояние – действие – субъекта) и получаем структуру простейшей системы управления.

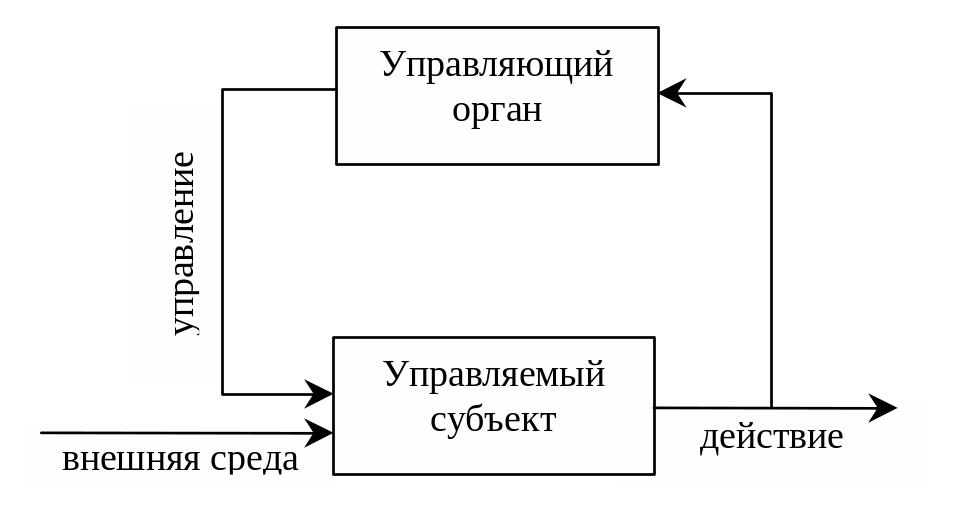
Рис. 3. Входо-выходная модель системы управления

Кто что выбирает из участников системы? Пусть состояние системы описывается действием агента , принадлежащим некоторому допустимому множеству A. Допустим, есть управление , принадлежащее множеству U. Пусть также есть критерий эффективности функционирования системы , который зависит от переменных, описывающих эту систему, т.е. от управления и от состояния системы. Мы будем пользоваться при описании предпочтений участников и при описании постановки задач управления скалярными моделями, т.е. считать, что все функционалы отображают множества в числовую ось: . Это значит, что многокритериальных задач мы рассматривать не будем – у них есть своя специфика.

Предположим, что известна реакция управляемого субъекта на то или иное управление. Пусть зависимость очень простая – состояние объекта является известной функцией от управления: , где () – модель управляемого субъекта, которая описывает его реакцию на управляющее воздействие. Коль скоро известна эта зависимость, если мы ее подставим в критерий эффективности функционирования, то получим функционал , который будет зависеть только от управления. Вот этот функционал называется эффективностью управления. Дальше задача заключается в поиске оптимального управления, то есть допустимого управления, обладающего максимальной эффективностью: . Это – задача синтеза оптимального управления, или просто "задача управления".

На первый взгляд все выглядит очень просто, в чем же заключается хитрость? Действительно, если все функционалы и множества известны, получим оптимизационную задачу, а решать ее – дело математики. Проблема заключается в том, что модель управляемого субъекта может быть очень сложной. По крайней мере, она должна быть сложной. Если мы описываем человека, группу, коллектив, организацию, предприятие, то понятно, что объект управления сложный, и модель должна быть адекватно сложной. Поэтому для того, чтобы перейти к детализации задачи управления, необходимо вернуться к построению модели управляемого субъекта. Математическим описанием поведения людей занимается теория принятия решений и теория игр. Поэтому, сделаем маленький экскурс в эти теории для того, чтобы понять, какого рода известными моделями мы можем пользоваться.