По способу управления.

Система делят по реализованному в них способу управления. Это: обыкновенная система, реализующая принцип регулирования по отклонению, с поиском экстремума, адаптивная. В каждом из этих классов можно выделить:

• Обыкновенные системы.

• Робастные системы. Предназначены для работы УУ обладающими неполными сведениями о системе (известны лишь границы изменения свойств объекта).

5. Общие сведения о моделях систем.

Модели элементов САР

Основным требованием, предъявляемым к моделям элементов системы, является удобство решения основных задач ТАУ. Прежде чем рассматривать модели элементов целесообразно рассмотреть эти задачи.

Основные задачи ТАУ:

1. Идентификация элементов и систем

Построение математической модели поведения системы, отражающей основные свойства системы, в форме, удобной для дальнейшего анализа и синтеза систем. Основная трудность при идентификации системы является определение модели обьекта управления. В общем случае данная задача пока не решена.

Любая математическая модель системы сначала представляет собой набор описаний элементов. Затем общее описание системы получают из описаний элементов

2. Анализ систем

Заключается в исследовании влияния параметров полученной системы на поведение этой системы.

Любая система работает в разнообразных режимах:

1. Установившийся режим. Анализ заключается в исследовании устойчивости установившегося режима (анализ устойчивости).

2. В установившемся режиме возникает задача анализа точности воспроизведения входного сигнала (анализ точности установившегося режима).

3. Переходной режим. Здесь возникает задача оценки качества переходного процессов в системе ( анализ качества переходного процесса)

1. Синтез систем.

Сводится к разработке системы, удовлетворяющей заранее заданным требованиям качества её поведения.

1. Система должна иметь значения показателей не хуже заданных.

2. Система должна иметь наилучшие свойства среди систем заданного класса.

Идентификация и синтез базируются на результатах анализа системы, но являются более сложными и до конца не решенными задачами.

6. Уравнения элементов сау

Д ля упрощения составления уравнений всей системы сначала необходимо рассмотреть уравнения элементов, путём решения задачи их идентификации.

Уравнения, описывающие поведение элементов, могут быть получены путём теоретических или экспериментальных исследований, либо их комбинаций. При теоретическом описании законы определяют поведение элементов (законы физики, химии, кинетики). Определяется как структура, так и свойства элементов. Уровень анализа элемента соответствует уровню описания дифференциальными уравнениями с сосредоточенными параметрами (сведёнными в точку). Можно попытаться теоретически описать все законы. Когда теоретически описать не удается, то элементы рассматривают как чёрный ящик.

Уравнение элементов составляются в два этапа.

На первом этапе описываются все особенности элементов, не заботясь о сложности получаемой зависимости. В общем случае это Нелинейные дифференциальные уравнения(ДУ.) Они могут быть представлены как:

а) уравнения вход- выход;

б) уравнения состояний

Уравнение вход- выход имеет вид

^{y(n) = G(y(n-1), ..., y, U(m), ...,U, F(n), ...F) 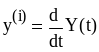возмущение m, r≤n.}

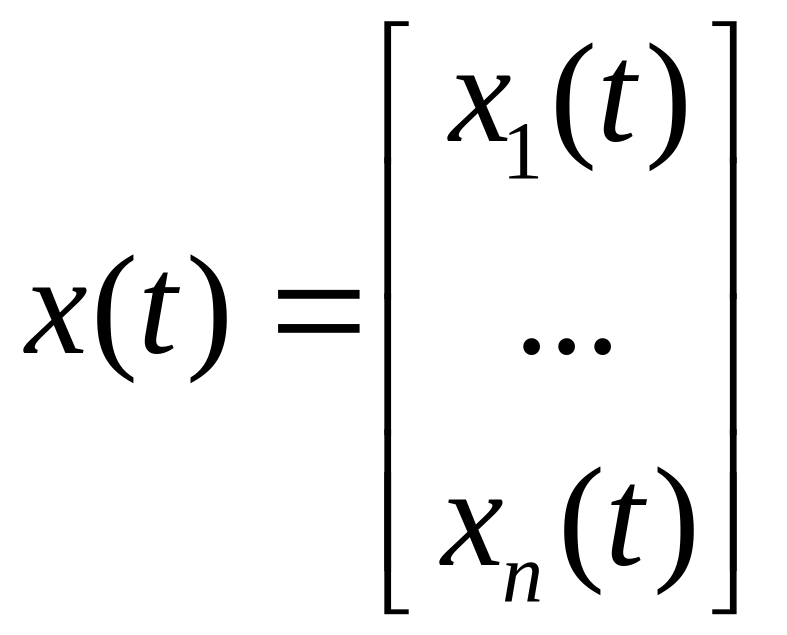
Рассмотрим вектор – уравнение состояния.

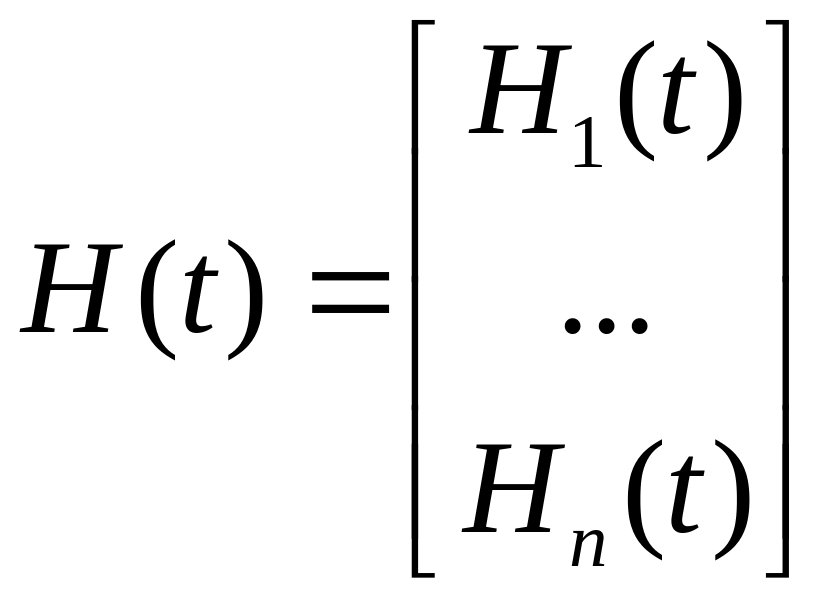Y=R(X,U). упрощают

На втором этапе дифференциальные уравнения(ДУ) упрощают. Упрощение состоит в том, что в уравнениях оставляют параметры, отражающие основные особенности поведения данной системы. Так получают упрощенную модель в виде ДУ. Далее полагают, что на её основе можно оценить всевозможные процессы, происходящие в элементе. Наиболее часто нелинейные ДУ упрощают до линейных. Замену нелинейных ДУ линейными называют линеаризацией.

В ТАУ разработано большое число приёмов линеаризации:

– линеаризация на основе гипотезы о малых отклонениях;

– гармоническая линеаризация;

– статистическая линеаризация и.т.д.

7. Линеаризация на основе гипотезы о малых отклонениях

–уравнение вход-выход.

В установившимся режиме:

Уравнения статики

Для линеаризации уравнения динамики представляют виде:

– отклонение выхода от установившегося значения.

– отклонение входа от установившегося значения.

– отклонение возмущения о установившегося значения.

При линеаризации ДУ:

Получили следующие уравнения

при

при

Используем при математическом исследовании ДУ.

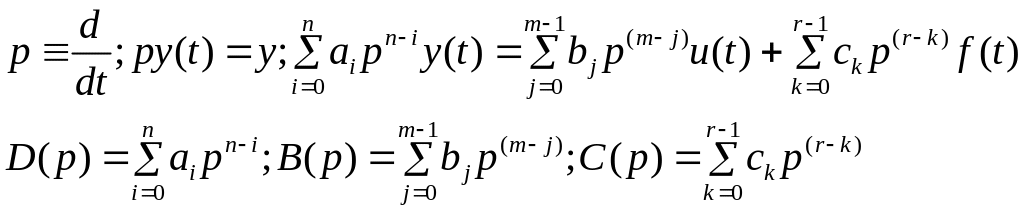
D(p),B(p),C(p) – линейные дифференциальные операторы полиномиального типа.

– характеристическое уравнение.

где – ОПФ по входу 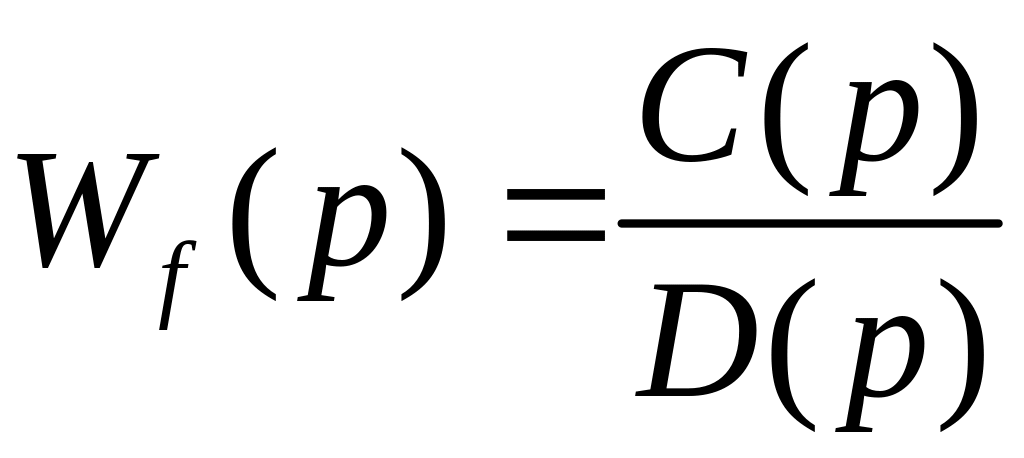– ОПФ по возмущению

Реально при описании ДУ стандартной формы:

1. все члены ДУ имеют размерность [y]

2. все члены ДУ имеют размерность [ ]

где k и k_f– коэффициент усиления по входу и по возмущению.

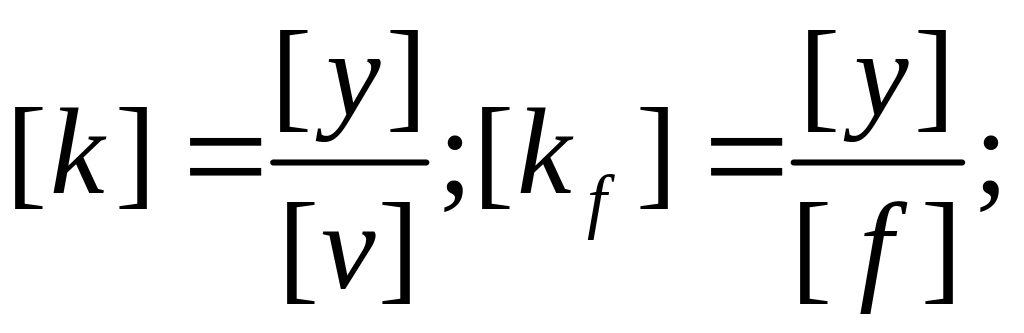
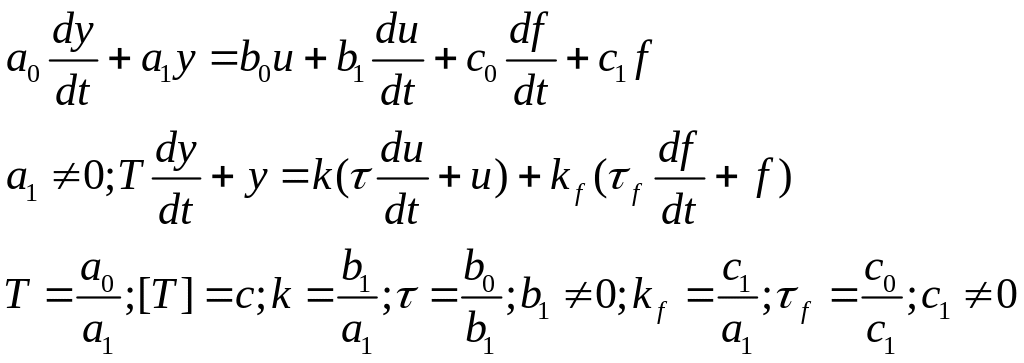Рассмотрим линеаризацию уравнений состояния

1. Установившийся режим .

Обозначим отклонения координат от их установившихся значений в виде:

Получим

– уравнение состояния

– уравнение выхода.

– матрица Якоби.

Аналогично

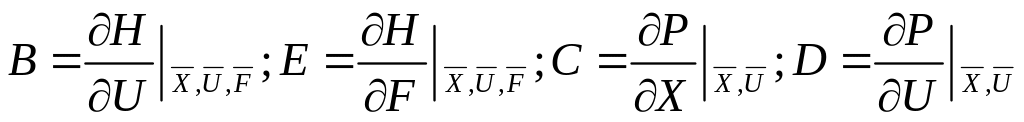
Если каждый из элементов системы описывается ДУ, то это не всегда удобно, т.к нужно искать уравнение входа выход всей системы. Вместо ДУ рассматривают их алгебраические аналоги, полученные путём алгебраизации ДУ. Обычно алгебраизация осуществляется на основе преобразования Лапласа.

8. Преобразование Лапласа

Преобразование Лапласа определяется для функции оригинала.

f(t) – оригинал, если удовлетворяет условиям:

1. 

2. имеет конечное число разрывов первого рода.

3. 

– абсцисса абсолютной сходимости.

– прямое преобразование Лапласа.

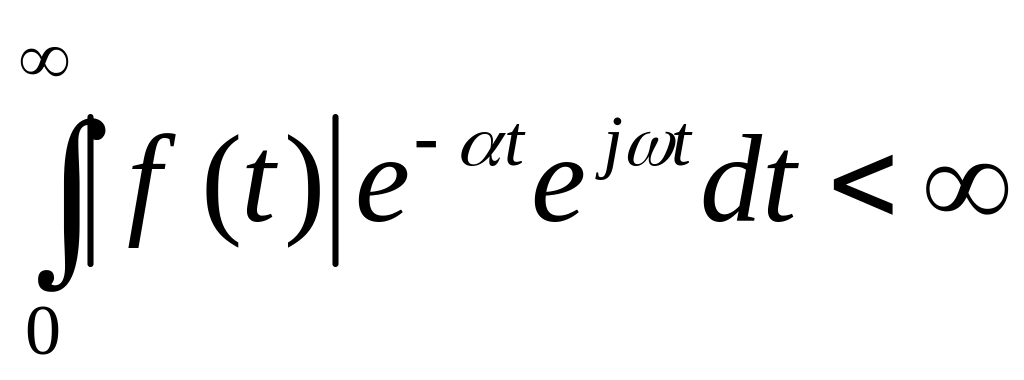, где – абсолютно интегрируема.

Для функции оригинала определено преобразование:

F(s) – изображение; f(t) – оригинал.

– обратное преобразование Лапласа.

Свойства преобразования Лапласа.

1. Линейность.

2. Изображения простейших функций.

   1. δ – функция Дирака.

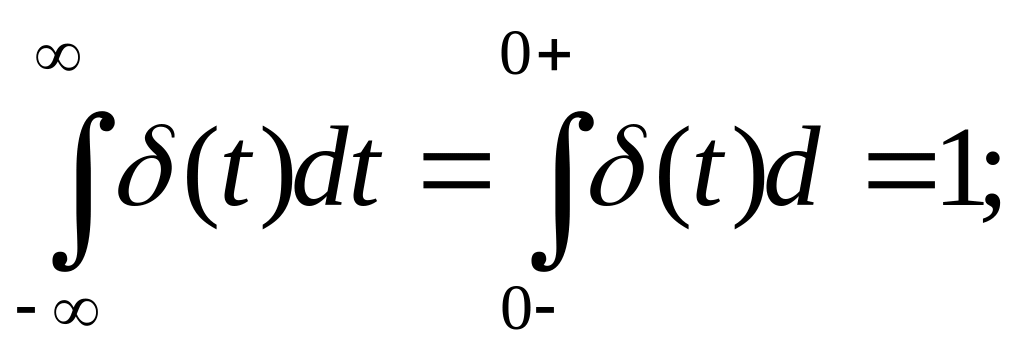
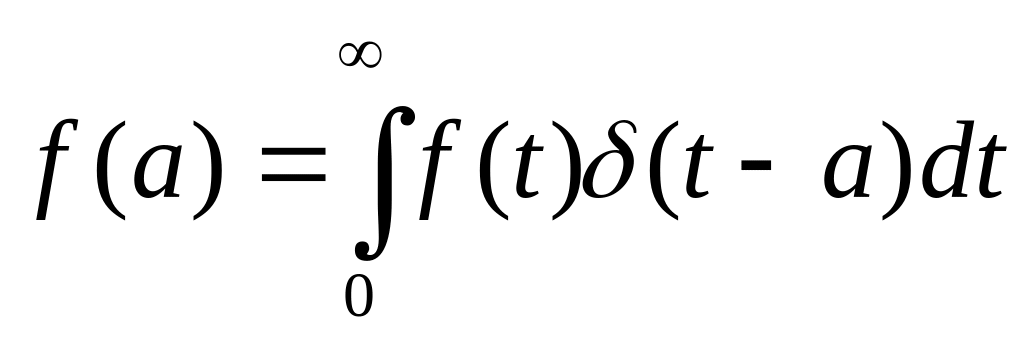
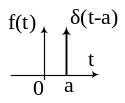
2. Единичный скачок.

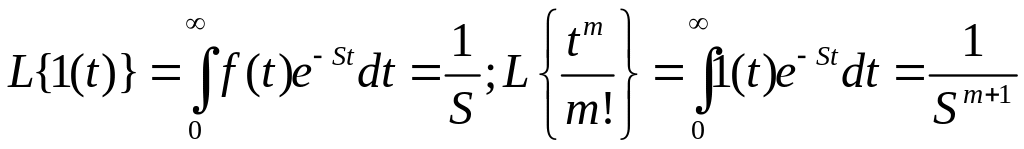
3. Изображение производной.

9. Передаточные функции элемента

;

;

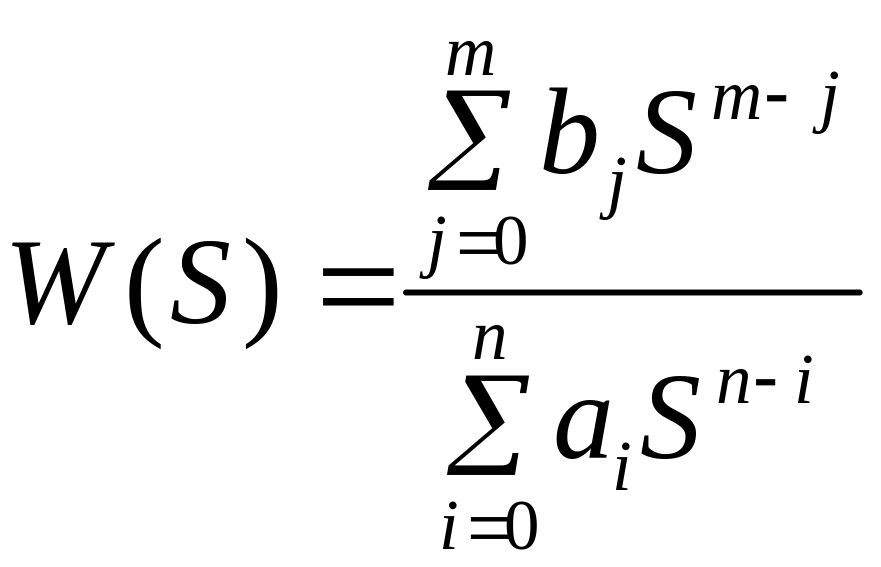– ПФ по входу 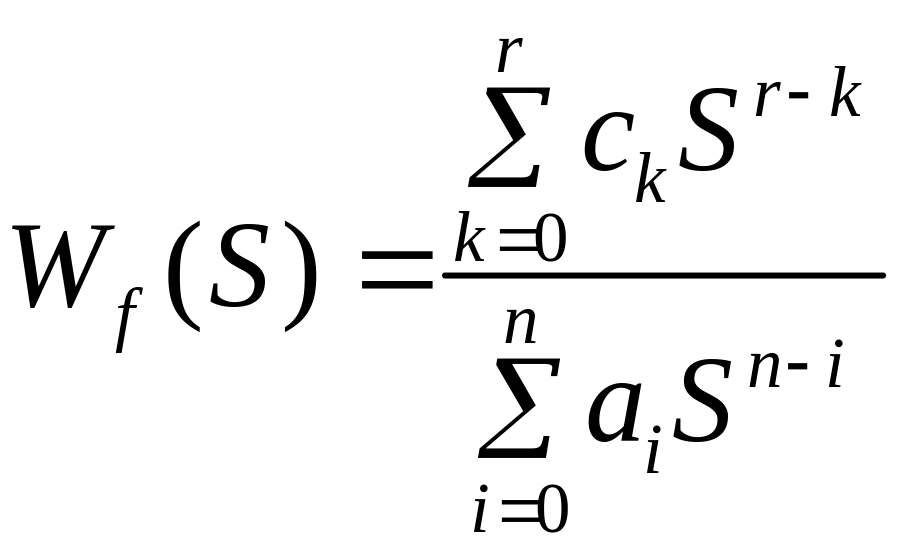– ПФ по возмущению

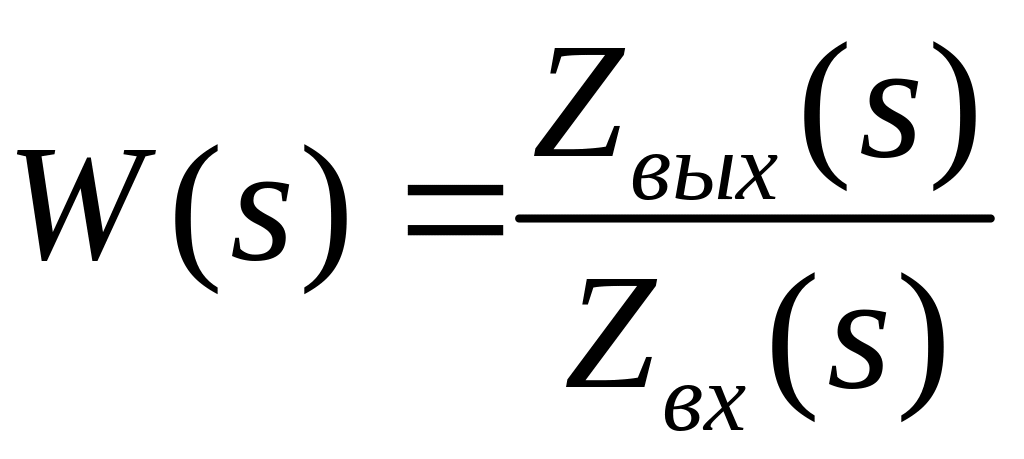
Каждая передаточная функция – это соответствующая форма записи ДУ, а знаменатель передаточной функции – характеристическое уравнение.

Передаточная функция легко позволяет найти сигнал на выходе элемента.

Операторный метод с помощью обратного преобразования Лапласа.

Структурные схемы элементов.

10. Правила преобразования структурных схем.

Г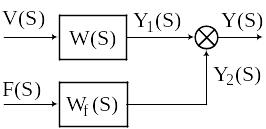 рафическое изображение элемента в виде блока с передаточной функцией по Лапласу в совокупности с сигналами отмеченными изображениями по Лапласу называется структурной схемой элемента. Система, состоящая из таких элементов с указанием направления сигналов, называется структурной схемой системы.

Для поучения передаточной функции системы приходится исключать отдельные элементы и их сигналы. Наиболее удобно это осуществляется по правилам преобразования структурных схем.

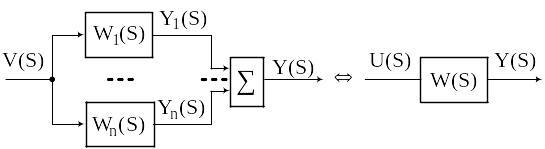
1. Замена последовательного соединения элементов.

Для нахождения передаточной функции соединения надо исключить все Ui().

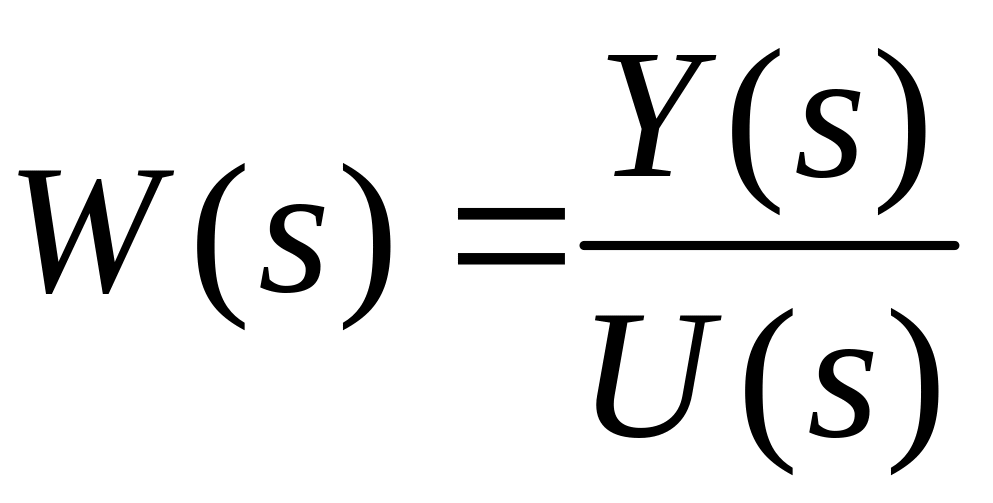
2. Замена параллельного соединения элементов.

3. Замена структуры с обратной связью.

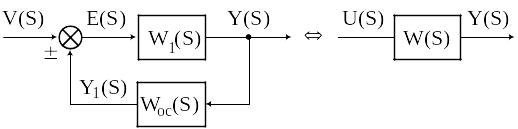
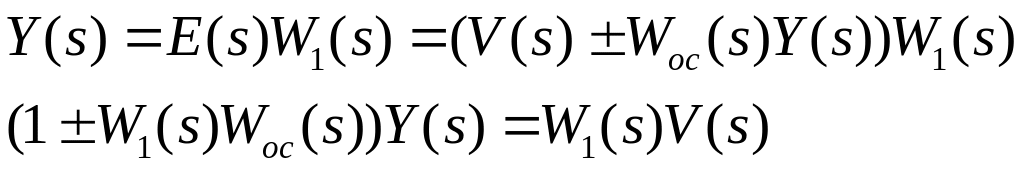
,где – передаточная функция замкнутого конура.

“+” – если ОС отрицательна.

“-” – если ОС положительна

4. Перенос точки съёма сигнала.

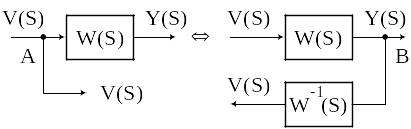
5. Перенос точки суммы сигналов.

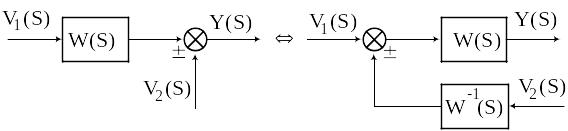
6. Правило Мэйсона: Используя эти правила можно любую сложную структуру свести каноническому простому виду.

где W(S) – передаточная функция разомкнутой системы.

Пример преобразования структурной схемы.

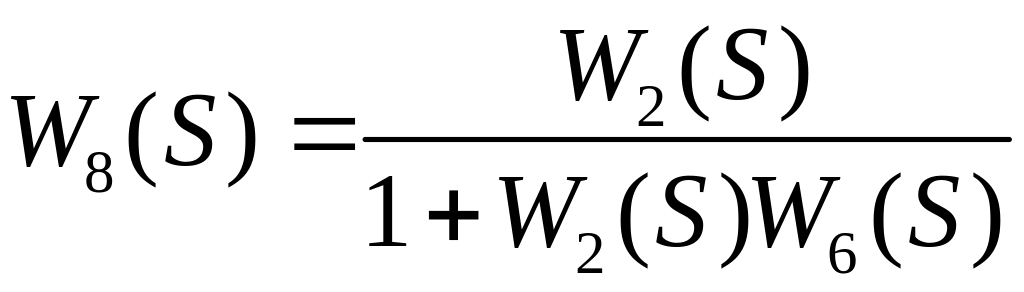
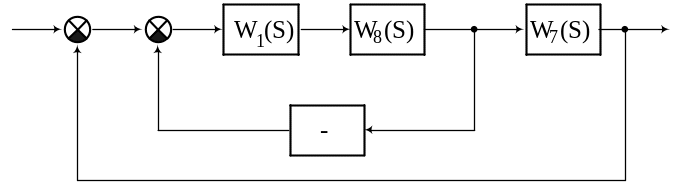
11. Сар двигателя постоянного тока.

Рассмотрим уравнение этой системы.

1. Напряжение на выходе потенциометра: Uv=k_ПV

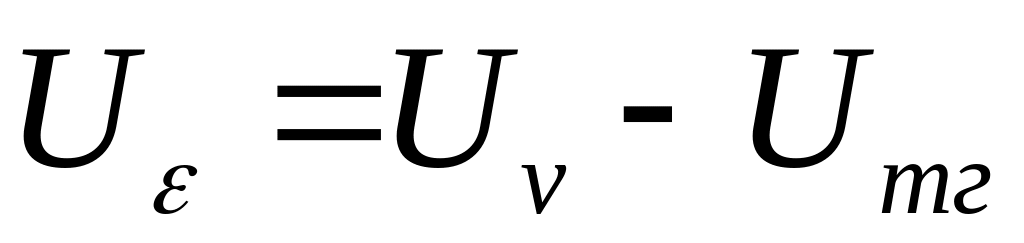2. , где Uтг – напряжение тактового генератора.

3. 

4. 

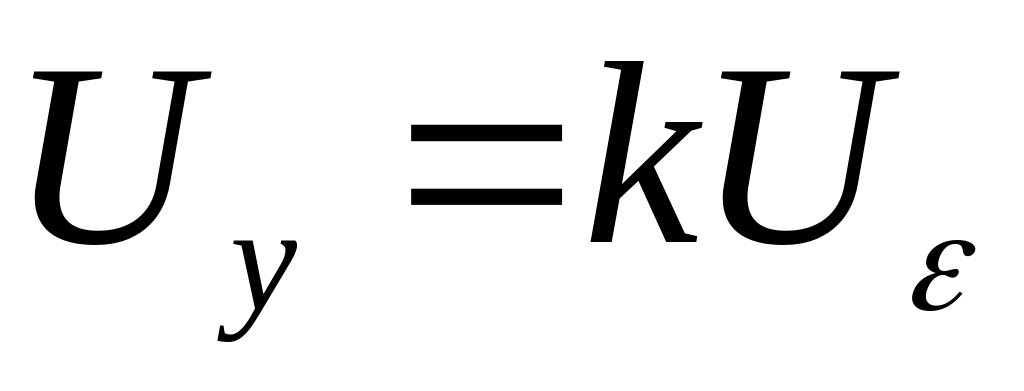
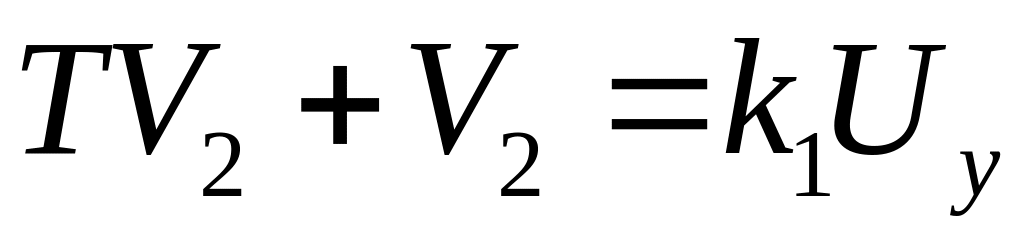
5. Уравнение двигателя:

6. 

;

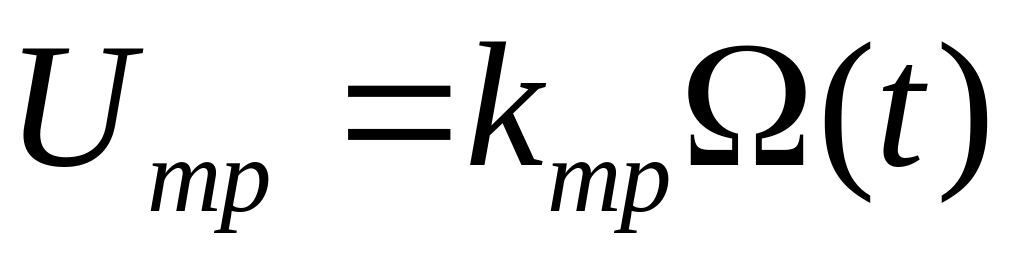
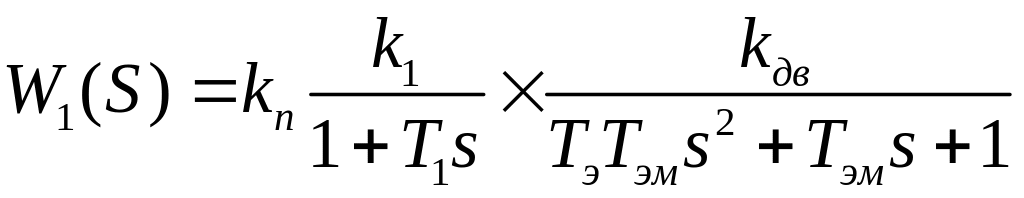
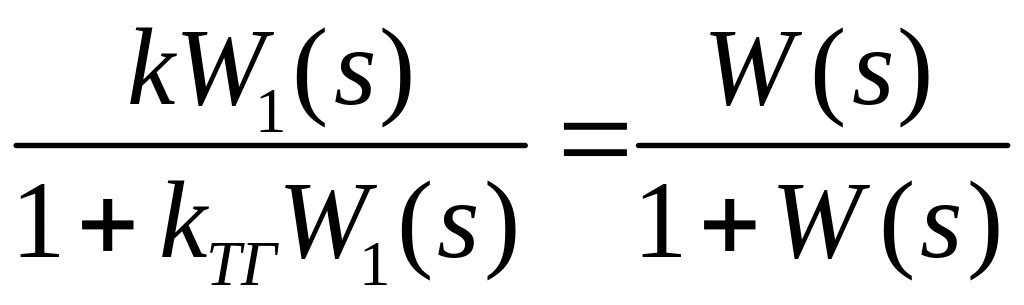12. Передаточная функция замкнутой системы

1. Передаточная функция разомкнутой системы.

2. Передаточная функция замкнутой системы.

3. Передаточная функция по ошибке.

В некоторых случаях на систему действуют возмущения, тогда используют общие модели:

4. Передаточная функция по возмущению.

характеризует ошибку от действия возмущения.

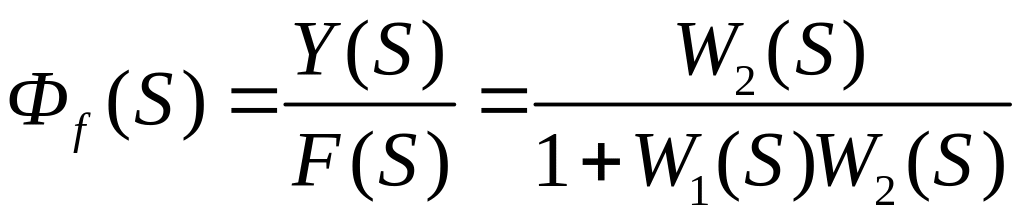
Все ПФ замкнутой системы имеют одинаковый знаменатель.

Характеристики системы.

13. Общие сведения о характеристика

Ранее рассмотрено описание систем с помощью передаточных функций:

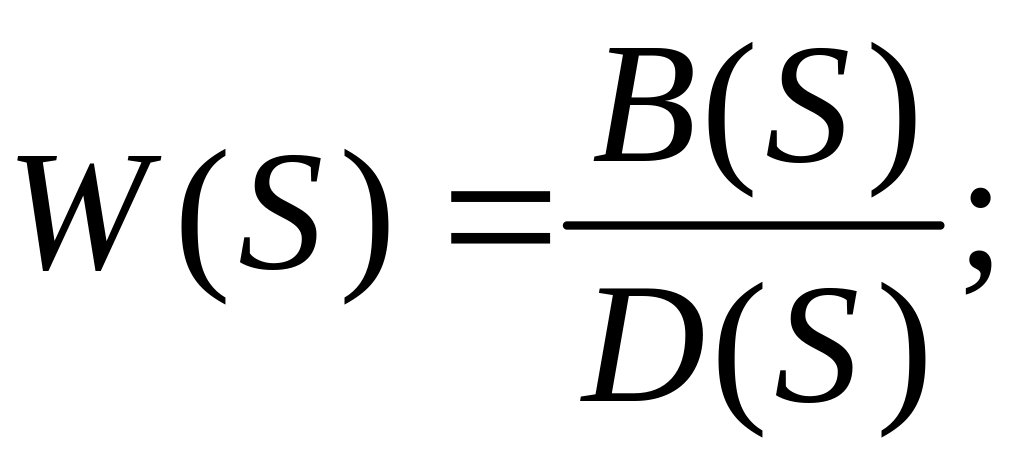
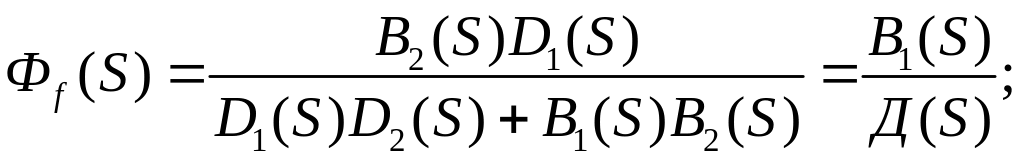
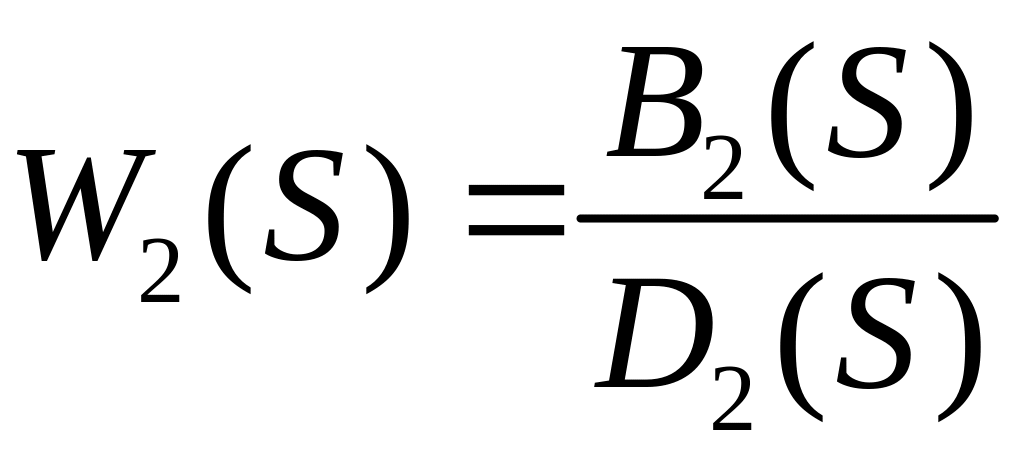
С помощью этих передаточных функций легко найти изображение:

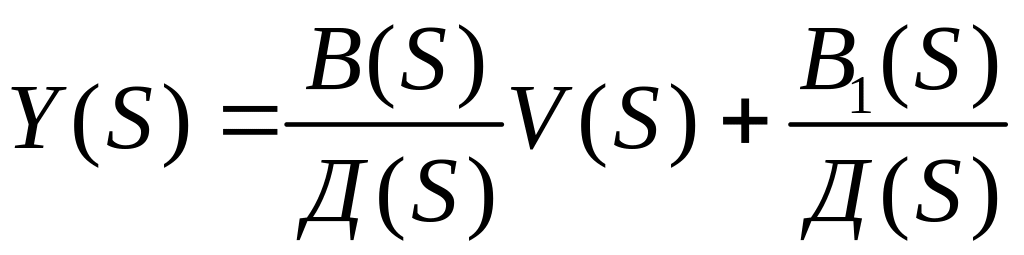
как решение ДУ

_{при нулевых начальных условиях.}

Возник вопрос: нельзя ли характеризовать систему с помощью отдельных решений ДУ, описывающего его поведение? Отдельные решения- это реакция системы на типовые входные сигналы,заданные либо во временной, либо в частотной области.

v(t) – сигнал, заданный во временной области . Реакция у(t)– временная характеристика.

V(jω) – сигнал, заданный в частотной области. Установившаеся реакция У(jw) – частотная характеристика.

Среди временных характеристик выделяют :

1. Импульсную переходную характеристику.

Это реакция на сигнал v(t)=δ(t),где

2. Переходную характеристику.

Это реакция на сигнал

Среди частотных характеристик обычно рассматривают амплитудно- фазовую АФХ, амплитудно- частотную АЧХ, и фазо- частотную ФЧХ характеристики. Входной сигнал

14. Переходная характеристика

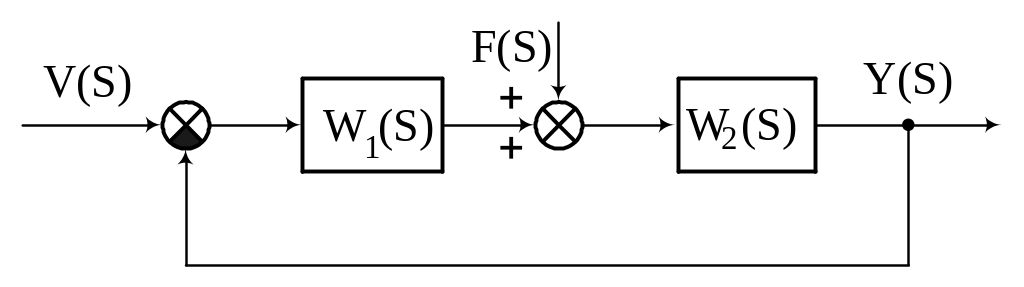
Рассмотрим систему, структурная схема которой показана на рис.

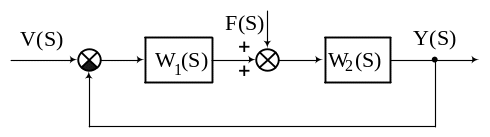
1. Переходная характеристика по входу.

.

Её можно наблюдать в этой системе, если:

2. Переходная характеристика по возмущению.

_{Её можно наблюдать в системе, если:}

Изображение по Лапласу ПХ по входу

Изображение по Лапласу ПХ по вомущению

По виду ПХ оценивают качество переходных процессов. Это важные характеристики систем.

15. Импульсная переходная характеристика

Пусть на вход системы подан сигнал, моделирующий дельта- функцию.

Модель дельта - функции:

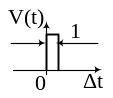
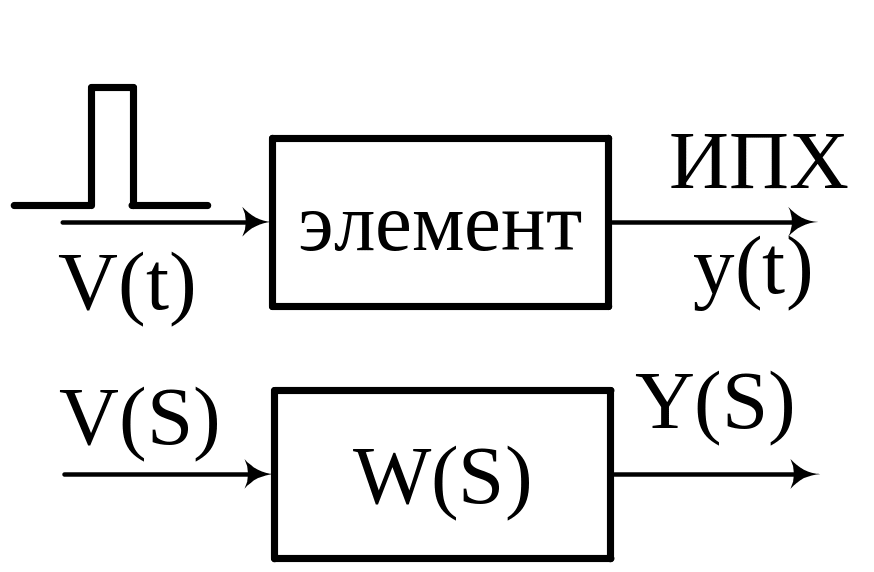
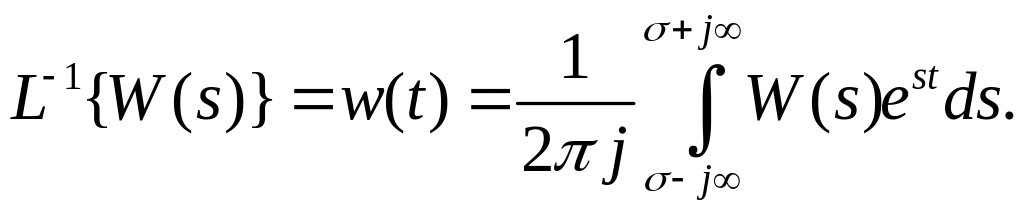
_{Рассмотрим связь ИПХ с переходной характеристикой.}

_{Переходная характеристика является интегралом от ИПХ, а импульсная переходная характеристика является производной от ПХ.}

16. Замкнутая система.

– ПФ разомкнутой системы.

– ПФ замкнутой системы.

– ПФ по ошибке.

– ПФ по возмущению.

Для каждой этой функции можно определить соответствующею ПХ:

17. Определение реакции системы на произвольный входной сигнал во временной области

Применим операцию L^-1 к левой и правой части уравнения.

(*)

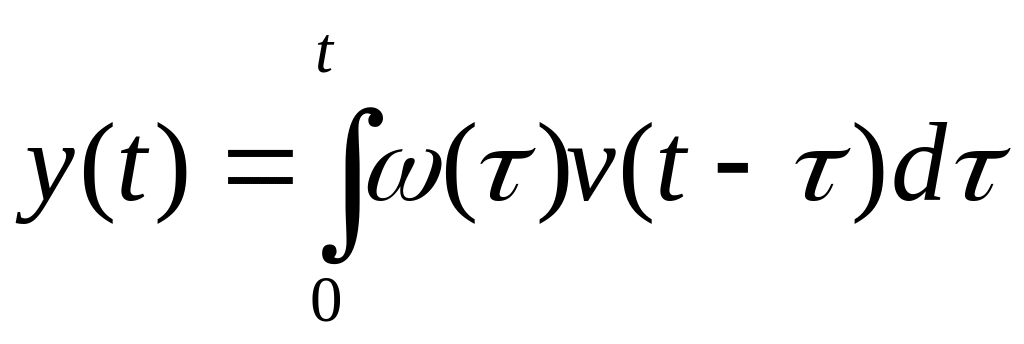Рассмотрим графическую интерпретацию интеграла свертки

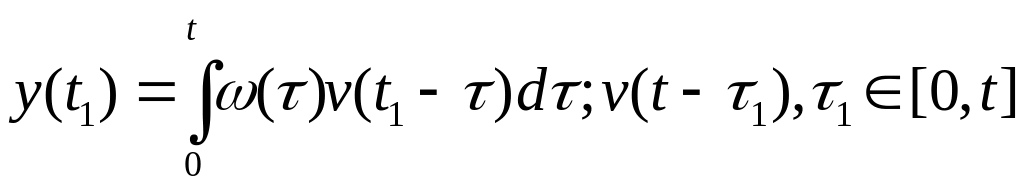
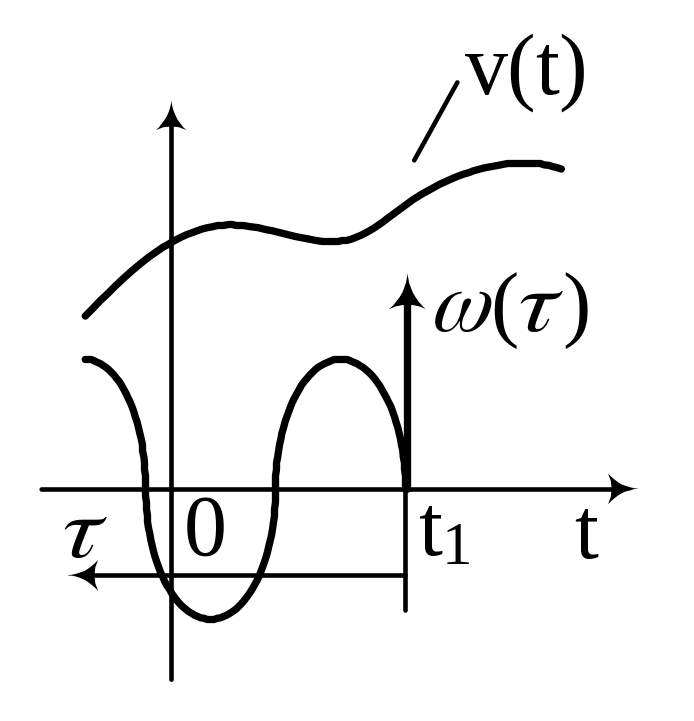
τ – “возрастает” ордината v(t) относительно t₁.

(*) определяет y(t) в тех случаях, когда y(0)=0. Если у(0) 0,то выражение

определяет реакцию на входной сигнал во временной области. При определении частотных характеристик и при исследовании систем при случайном воздействии используют описание реакции на входной сигнал в виде интеграла свертки.

18. Основные свойства импульсных переходных характеристик

1. Условие физической реализуемости.

Если это условие не выполняются, то нарушаются причинно следственные связи – ИПХ появляется раньше δ-функции- причины появлентя ИПХ на выходе системы.

2. Условие устойчивости элементов или системы по входу.

Систему называют устойчивой по входу, если для каждого ограниченного входного сигнала её реакция ограничена.

Доказательство:

Необходимое условие:

t) – ограниченный входной сигнал.

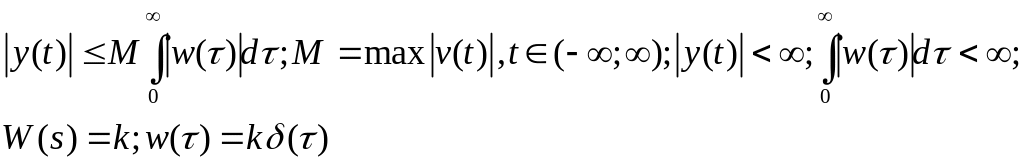
3. ИПХ соединений.

   1. Последовательное соединение.

2. Параллельное соединение.

19. Частотные характеристики

1. Ч астотные характеристики разомкнутой системы или элементов.

-гармонический сигнал.

Если система устойчива по входу, то при гармоническом входном сигнале её выход в установившемся режиме также будет гармоническим.

T – практическая длительность переходных процессов или интервал памяти.

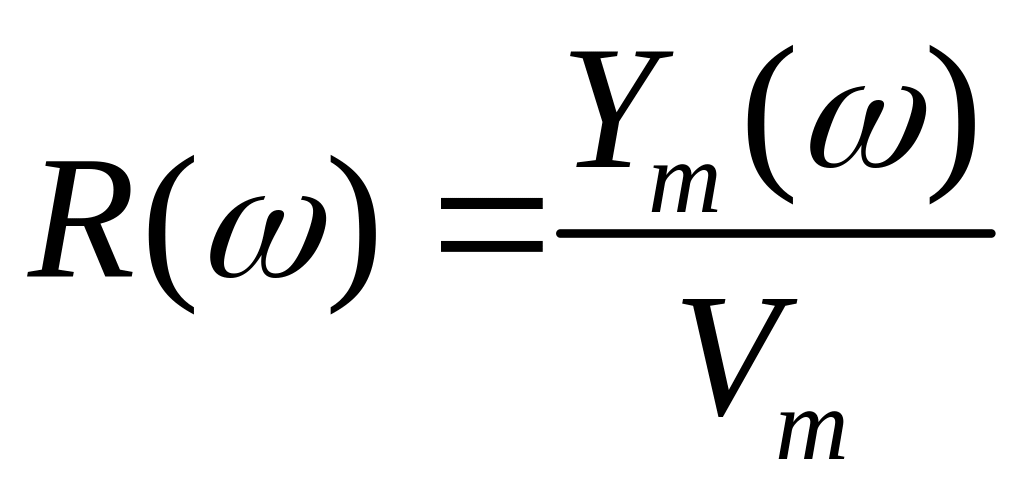– АЧХ;

– ФЧХ.

Использовать две характеристики (АЧХ и ФЧХ) неудобно, поэтому объединим их в одну АФХ:

Выразим yуст через параметры АФХ:

– обобщенный гармонический сигнал.

, где

Рассмотрим связь АФХ с ПФ и ИПХ:

;

;

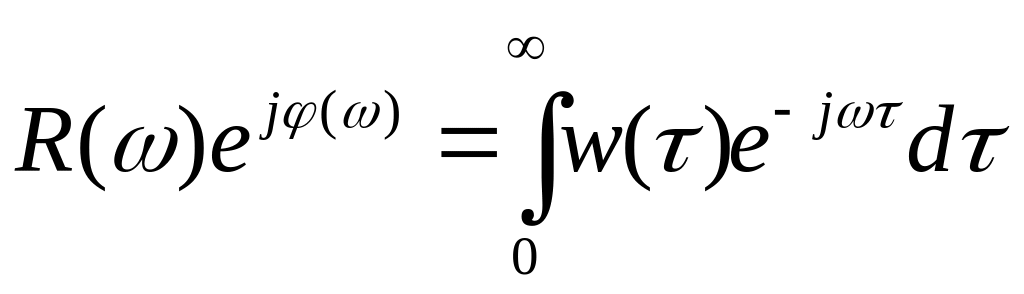– АФХ системы или элемента.

– определяет ПФ.

– преобразование Фурье ПХ.

При решении различных задач кроме показательной формы используют их алгебраические выражения

;

– вещественная частотная характеристика;

– мнимая частотная характеристика.

Для минимально- фазовых систем (если все нули и все полюсы “левые”) вид одной определяет другую. Они связаны с помощью преобразований Гильберта.

2. Частотные характеристики замкнутой системы

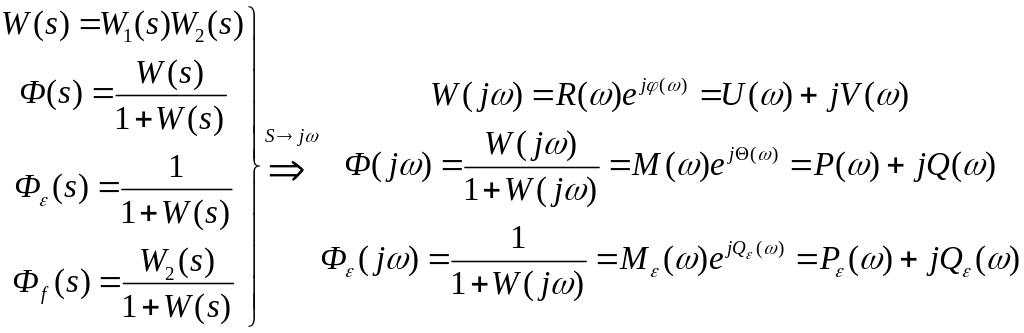
ЧХ позволяют исследовать установившиеся процессы.

Уравнения состояния

В некоторых случаях удобно описывать систему с помощью уравнений состояния. При описании систем и элементов в пространстве состояний рассматриваются векторы: а) - вектор координат состояния;

б) - вектор управлений (входов);

в) -- вектор выходов.

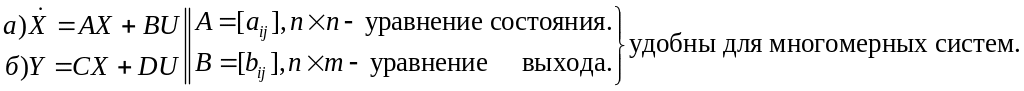
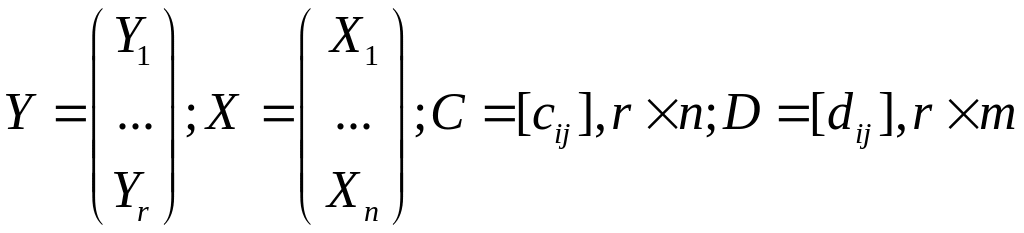
где Ф(S) – матричная передаточная функция.

Многомерные системы удобно описывать уравнениями состояния:

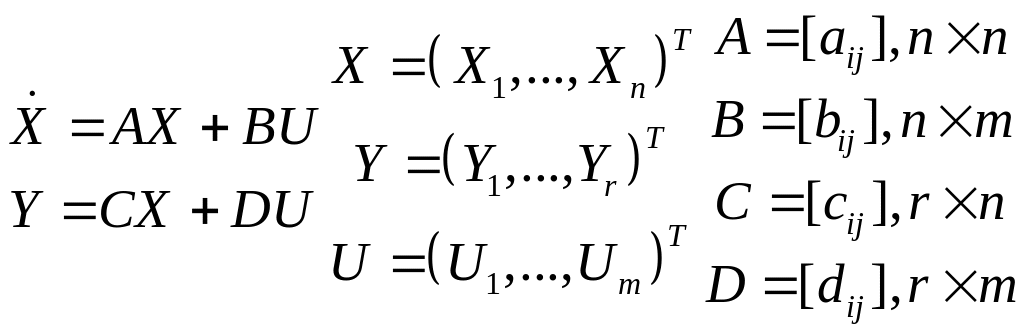
Х – вектор состояния. При использовании нормальной формы Коши записи ДУ ; U – вектор управления, Y – вектор выхода.

A- системная матрица, B – матрица входа, С и D – матрицы выхода. Часто D=0, при этом: Координаты состояния можно изменять с помощью преобразования подобия матриц:

X -новые координаты состояния. Уравнения примут вид

Преобразования подобия не меняют собственные числа матриц.

– собственные числа (значения) матрицы А, являющимися корнями характеристического уравнения.

Покажем, что преобразования подобия не меняют собственные числа матрицы

.

При исследовании систем используется алгебраизация уравнений состояний с помощью преобразования Лапласа.

X(0) – вектор начальных условий.

Для определения матричной передаточной функции выразим X(s) из 1-ого уравнения

– матричный экспоненциал- матрица Коши.

– матричная передаточная функция.

– матричная АФХ системы.

При исследовании системы по уравнениям вход - выход частотные характеристики представлены не только виде АФХ, АЧХ, ФЧХ, но в виде логарифмических характеристик ( ЛЧХ). Используют логарифмический масштаб по оси абсцисс и по оси ординат.

20. Логарифмические частотные характеристики

1. Логарифмические масштабы

W(jω)=R(ω)e^jφ(ω)

lnW(jω)=lnR(ω)+jφ(ω)

часть завис. завис.

от АЧХ от ФЧХ

В качестве логарифмического масштаба оси частот используется lg ω.

lg2≈0.3 lg3≈0.5 lg5≈0.7

масштаб по осям нелинейный.

L(ω)=20 *lgR(ω)=20 *lg|W(jω)| (дБ)

L(ω)- построенная с использованием логарифмического масштаба частот- называется ЛАЧХ.

Стандартные наклоны используются при построении асимптотических ЛАЧХ.

Фазовая характеристика:

φ(ω), построенная с использованием логарифмического масштаба частот по оси абсцисс и обычного масштаба по оси ординат называется ЛФЧХ-логарифмической фазочастотной характеристикой.

21. Логарифмические характеристики разомкнутой одноконтурной системы.

В этой системе отсутствуют контуры местной ОС.

W₅(s)=W_2­(s)+W₃(s)

W(s)=W₁(s)∙W₅(s) ∙W₄(s) W(s)= -типовая форма ПФ разомкнутой одноконтурной системы.

(j ω W)=R₁(ω)e^jφ1(ω)… R_n(ω)e^jφn(ω)_­= R_i(ω)e^jφ(ω)= R(ω)e^jφ(ω)

φ(ω)= φ_i(ω); R(ω)= R_i(ω) L(ω)=20lgR(ω)= L_i(ω)

L_i(ω)=20lgR_i(ω); i=1…n φ(ω)==argW(jω)= φ_i(ω

В системе может быть контур с местной ОС:

W(jω)= -

ПФ соединения с ОС

R(ω)=|W(jω)|=

L(ω)=20lgR(ω)=20lg|W₁(j ω)|-20lg|1+W₁(j ω)W₂(j ω)|=L₁(ω)-L_k^/( ω)

L₁(ω)=20lgR₁(ω)

L_k^/(ω)=20lg|1+W_k(jω)|, где W (j )=W (j ω)W (j ω).

L_k^/(ω)=

22. ЛЧХ типовых сомножителей

В качестве типовых рассматривают сомножители W₁(s)=k/s^ν; W₂(s)=(Ts+1)^m _{, = 0; 1; 2;… m= 1; 2;…}

W₃(s)=(T²s²+2ξTs+1)ⁿ, n= 1; 2;…

АФХ сомножителя первого типа

W₁(jω)=k/(jω)^ν;

где k- коэффициент усиления, ν- порядок астатизма

k>0; ν=0; ±1; ±2 показатель степени

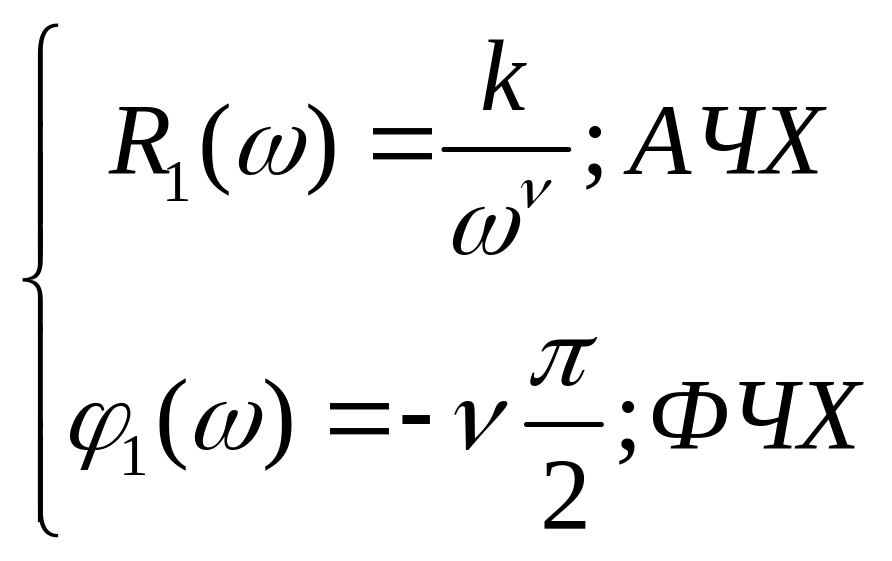
1 .W₁=30

L₁(l)=20 lg(30)=30 дB

W₂(S)=40/s²; 20lg40=32 дВ; ; ν=2

W₃(s)=30 *s; ν=-1

Если изменять K, то все прямые будут подниматься при увеличении K и опускаться при уменьшении K, не изменяя наклона.

б) Cомножитель второго типа имеет ПФ W₂(s)=(Тs+1)^m

T>0; m=±1; ±2;…

W₂(jω)=(1+jωT)^m=( )^m∙е^{jm∙arctg(ωT)}

j=

L₂(ω)=20m∙lg( ) . Если задаваться частотой

ω € (0, ), то выражение L₂(ω) определяет точную ЛАЧХ.

Вместо точной удобнее пользоваться асимптотической ЛАЧХ,составленной из отрезков асимптот.

1. Левая асимптота:

ω<1/T , (ωT)² « 1

L_2а(ω)= 20m lg =0

2. Правая асимптота:

ω 1/T , (ωT)² » 1

L_2b(ω)= 20m lg =20m lg(ωТ)- прямая с наклоном +20m дB/дек;

φ(ω)= m arctg(ωT).

Точная ЛAЧХ L₂(ω) будет отличаться от асимптотической, | L_2a(ω)-L₂( )| 3m дВ

в) W₃(s) = (T²s²+2ξTs+1)ⁿ; [T]=c; ξ- показатель колебательности, ξ € (0,1). Уравнение

T²s²+2ξTs+1=0

имеет корни s_1,2=-ξ ω₀±j ω_{0 ,} где ω₀=1/T.

При ξ>1 многочлен допускает разложение

T²s²+2 ξTs+1=(T₁s+1)(T₂s+1),

Где - 1/T₁, -1/ T₂ – вещественные корни уравнения. При ξ=1 => T₁=T₂. АЧХ

W₃( ω) =

ФЧХ

^φ₃(ω)= n arc tg . ЛАЧХ

L₃(ω)= 20n lg

^φ₃(ω)= n arc tg

при ω € (0, ) определяют точные ЛЧХ.

Асимптоты ЛАЧХ

L_3a(ω)= 20m lg 1=0 при ω<1/T; (ωT)²«1

L_3б(ω)= 40n lg ω>1/T;

L₃(1/T)=20n lg(2ξ)

При построении ЛЧХ разомкнутой системы нужно:

1. Построить L(ω)=

2. φ(ω)= и построить график.

Правило построения асимптотической ЛАЧХ разомкнутой одноконтурной системы:

1. Определяются коэффициент усиления, порядок астатизма и все сомножители 2-го и 3-го типа (к, ν, m_k,n_k).

2. Для каждого сомножителя определяются сопрягающие частоты:

m=>ω_k=1/T_k; n_k=> ω_k=1/T_k - сопрягающие частоты, которые отмечают на оси ω.

ω_k1< ω_k2< …<ω_kN

3) Строится НЧ участок ЛАЧХ ω≤ω₁=min ω_k1

a) на частоте ω=1 c^-1 откладывается ордината 20 lgk.

Через полученную точку проводится прямая с наклоном -20 ν д Б/дек.

Отрезок этой прямой в области НЧ является НЧ участком ЛАЧХ.

4) На каждой из сопрягающих частот наклон прямой изменяется на 20m дБ/дек, если ω_к1 обусловлена сомножителем (Тs+1)^m , либо на 40n дБ/дек , если ω_к2 обусловлена сомножителем (Т² s²+2ξTs+1)ⁿ

5) При необходимости при малых ξ_k, в области сопрягающих частот, обусловле- нных сомножителями 3-го типа, в асимптотическую ЛAЧХ вводят поправки.

Примеры:

1. W(s)=10/(2s+1)

W₁(s)=10/s⁰; k=10; ν=0;

T=2c; ω=1/2=0,5 c^-1

2) W(s)=

K=0.5; ν=-1; m=-2; T=0.01 c; 20lg0.5=-6 dB.

ω=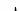 1/Т=100 c

φ(ω)=π/2-2arctg(0.01ω)

3) W(s)=

к=50; 20 lgk=34 дБ;

ν=1; ω₁=1/1.4=0.7 c^-1; ω₂=1/0.5=2 c^-1; ω₃=1/0.05=20 c^-1; .

T=0.05 c; ξ∙0.1=0.07=> ξ=0.7

.

φ(ω)=-π/2-arctg(1.4 ω)+arc tg(0.5ω)- arctg(0.07ω/(1-0.0025 ω²)).

Звенья САР.

23. Понятие о звене.

Систему рассматривают с физической точки зрения, как соединение элементов. Элементов, входящих в САР, достаточно много. При исследовании системы интересуются не физическим содержанием ее элементов, а прежде всего их ДУ .

Число уравнений, которые описывают элементы, не так уж велико. Некоторые из уравнений выбраны в качестве типовых. Так возникло понятие «звено»- как часть системы, описанное типовым ДУ.

При делении модели системы на части-звенья может оказаться, что один элемент может описываться как одним звеном, так и соединением нескольких звеньев. Не исключено, что одним звеном можно представить и соединение нескольких элементов. Типовым ДУ соответствуют типовые звенья.

Типовые звенья:

Однозначных установок для обьявления звена типовым не существует. Одним из примеров может служить следующий перечень звеньев, взятых в качестве типовых:

1. Усилительное звено.

2. Апериодическое звено 1-го порядка.

3. Апериодическое звено 2-го порядка.

4. Колебательное звено.

5. Консервативное звено.

6. Идеальное дифференцирующее звено.

7. Идеальное интегрирующее звено.

8. Звено запаздывания.

9. Неустойчивое звено 1-го порядка.

Рассмотрим подробно все характеристики этих звеньев.

24. Усилительное звено

Уравнение звена y(t)=kv(t), k- коэффициент усиления звена. Передаточная функция W(s)=k, w(t)=L^-1{W(s)}=k∙δ(t) – ИПХ

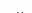W(s)=k

h(t)=

_{Графики импульсной переходной и переходной характеристик показаны на рис.}

АФХ: W(jω)=k; вещественная частотная характеристика U(ω)=k; мнимая частотная характеристика V(ω)=0. Логарифмические частотные характеристики показаны на рис.

25. Апериодическое звено 1-го порядка

Ty^/+y(t)=kV(t); k- коэффициент усиления

Т- постоянная времени. (Т>0)

Характеристическое уравнение имеет 1 корень:

Ts+1=0; s₁=-1/T<0

ПФ: W(s)=

ИПХ: W(t)= L^{-1 =}ke^-t/T

ПХ: h(t)= (1-e^-t/T)

АФХ:

W(jω)=

U(ω) V(ω)

W(jω)=

φ(ω)=- arctg(ωT)

На комплексной плоскости АФХ имеет вид, показанный на рис.

Л ЧХ звена имеют вид

L(ω)=20lgk - 20lg

φ(ω)= -arctg(ωT)

26. Апериодическое звено 2-го порядка

Звено соответствует ДУ 2-го порядка

T²y^//+2ξTy^/+y(t)=kV(t);

к- коэффициент усиления, Т- постоянная времени, ξ- коэффициент колебательности, ξ≥1 .

Характеристический многочлен допускает представление произведением 2-х сомножителей, т.е.

Т²s²+2 ξTs+1=(1+T₁s)(1+T₂s)

T₁T₂=T²; T₁+ T₂=2ξT; T₁>T­₂ (ξ=1, T₁=T₂)

ПФ: W(s)=

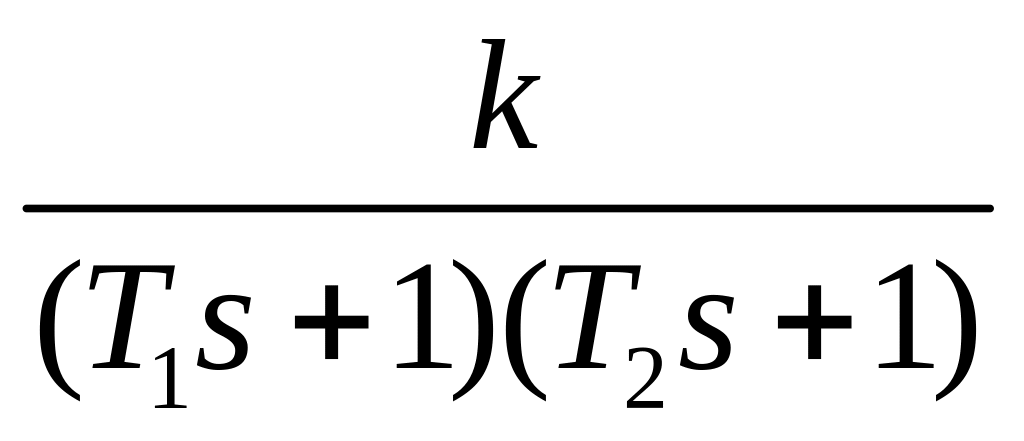
ИПХ: W(t)=L^{-1 =}

График переходной характеристики показан на рис.

АФХ: W(jω)=

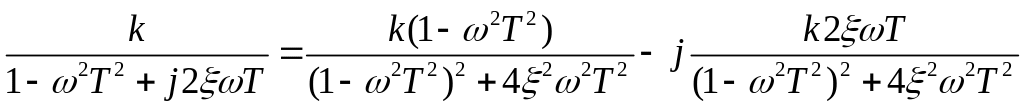
ЛЧХ звена определяются выражениями

L(ω)=20lgk - 20lg

φ(ω)= -arctg(ωT₁) -arctg(ωT₂)

27. Колебательное звено

ДУ звена

T²y^//+2ξTy^/+y(t)=kX(t); 0<ξ<1

Характеристическое уравнение

T²s²+2ξTs+1=0

Имеет комплексно- сопряженные корни

s_1,2=ω₀(-ξ±j ),

где ω₀=1/T- собственная частота колебаний.

W(s)= 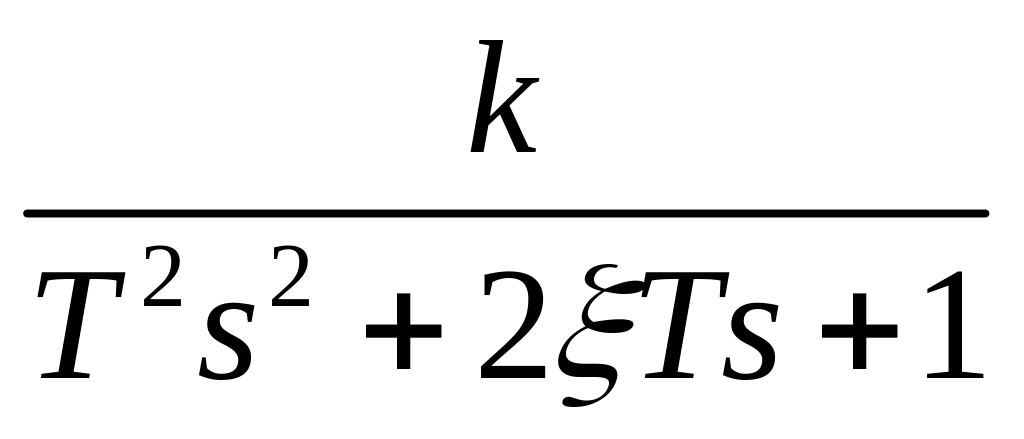-ПФ звена , ИПХ: w(t)=L^-1{W(t)}=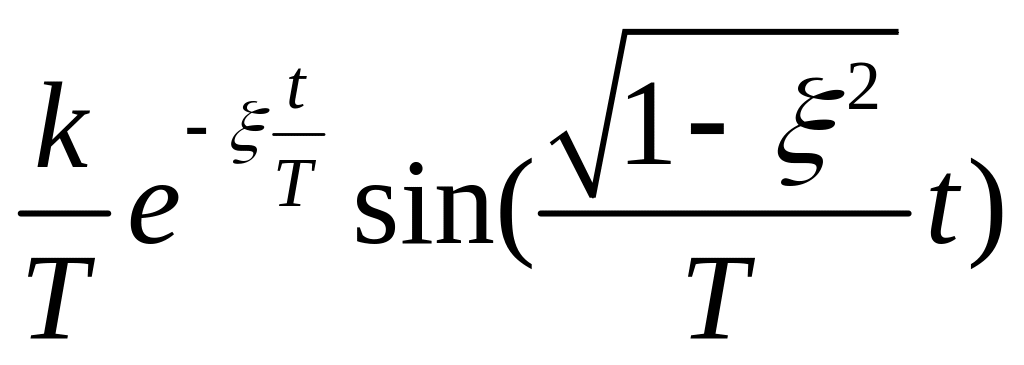

ω_д= - частота демпфированных колебаний,

T_д=2π/ω_д -период демпфированных колебаний.

Переходная характеристика

h(t)=L^-1{W(s) }=k(1-

=arctg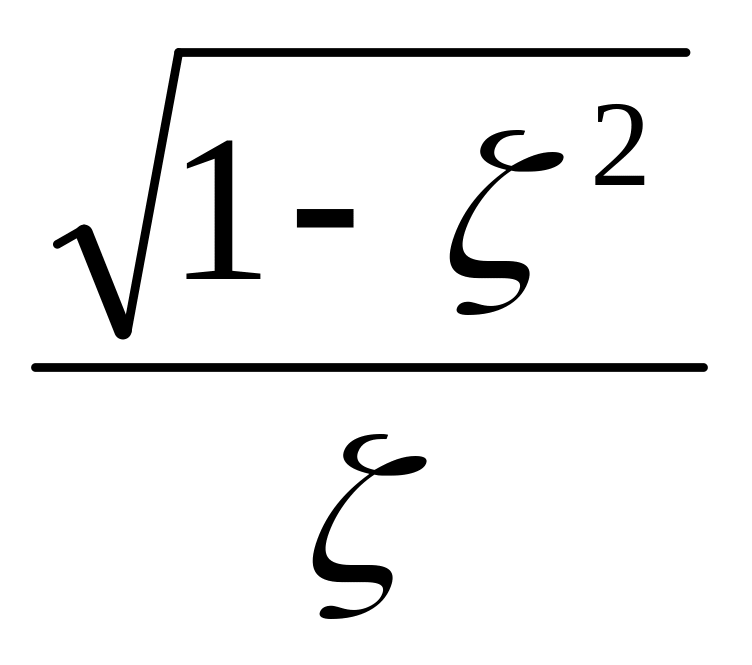 А₁/A₂=f(ξ) При ξ= 0.707 получается ПХ наилучшего вида, называемым техническим оптимумом.

W(jω)=

L(ω)=20lgk-20lg

28. Консервативное звено.

T ²y^//+y(t)=kV(t) ξ=0

Характеристическое уравнение

T^2­s²+1=0

имеет чисто мнимые корни s_1,2=±j

_ПФ

W(s)=

ИПХ

w(t)=L^-1{ }=

ω₀=1/T T₀=2π/ ω₀ =2 πT- период колебаний.

ПХ: h(t)= =k(1-cosω₀t)

Частотные характеристики:

АФХ: W(jω)=

U(ω)= ; V(ω)=0

ЛЧХ L(ω)=20lgk-20lg

φ(ω)=

U_y=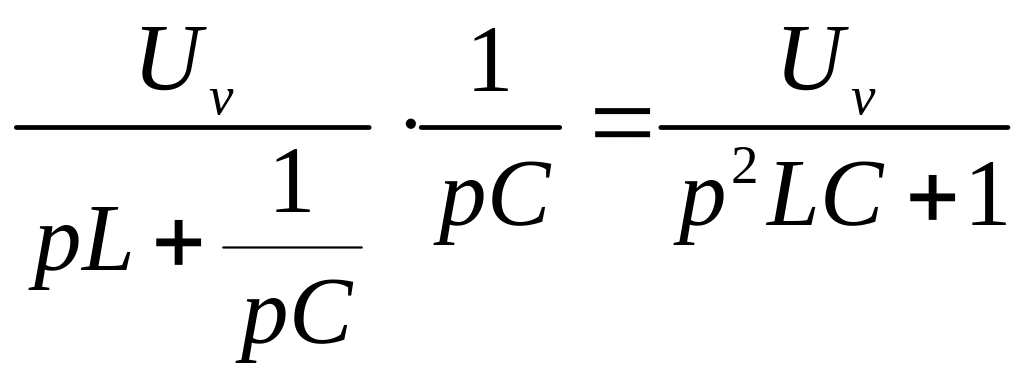

T²=LC

29. Идеальное дифференцирующее звено.

T =y(t)

W(s)=Ts

Звено является физически нереализуемым. Физически реализуют ПФ

W(s)=

-cчитаемую как реальное дифференциальное звено.

T₂<<T₁

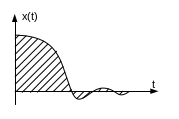
w(t)=L^-1{Ts}=TL^-1{s∙1};w(t)=T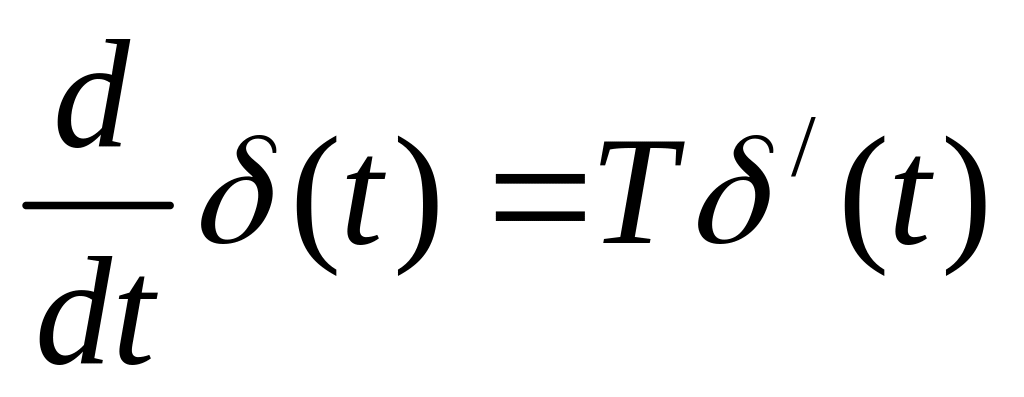

δ( t)=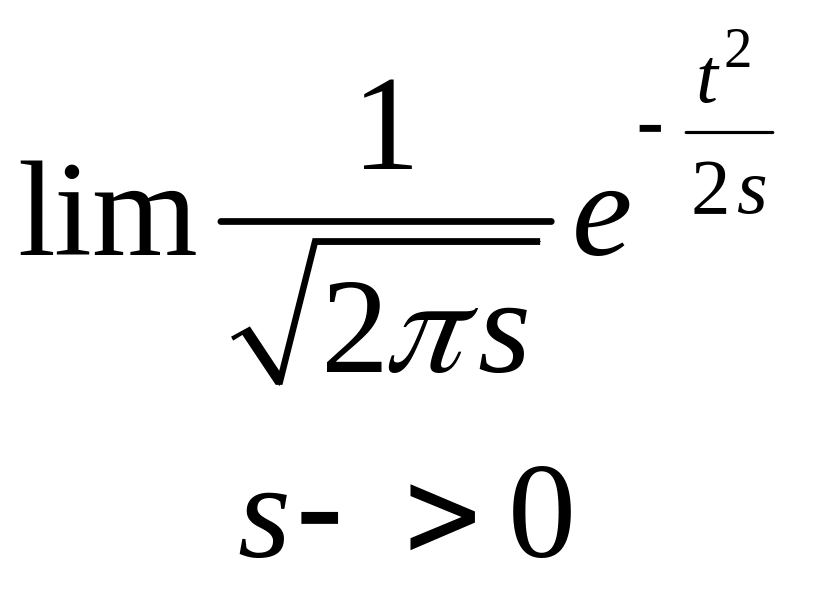 - гаусовская кривая

h(t)=T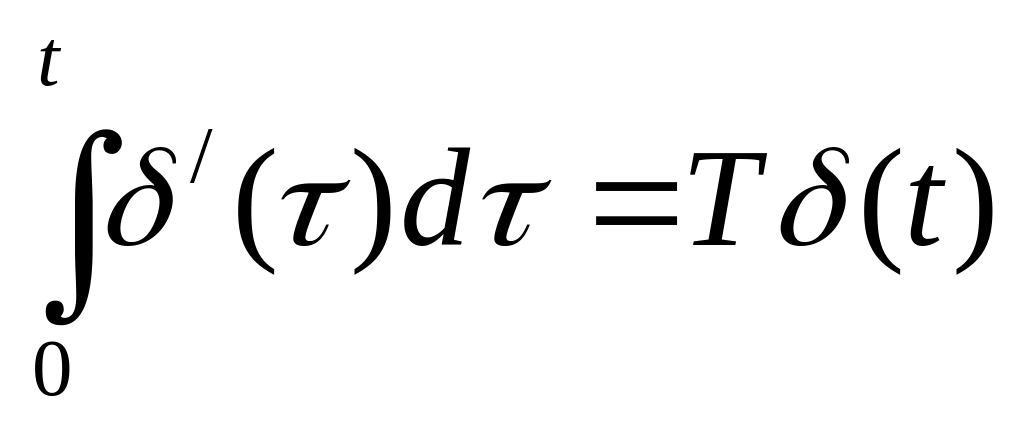

W(jω)=jωT

-совпадает с положительным направлением мнимой оси.

L(ω)=20lg ωT; φ(ω)=π/2

-ЛЧХ звена. Их графики показаны на следующем рис.

30. Идеальное интегрирующее звено

Уравнения интегрирующего звена в интегральной

а) y(t)=k_u

и б) Ty^/(t)=V(t)

- дифференциальной формах. Характеристическое уравнение Ts=0 имеет корень s=0. ПФ

W(s)=K_u/s; k_u=1/T; [k_u]=C^-1,

Из уравнений звена следует, что размерности входа и выхода звена одинаковы,т.е.

[V]=[y]; k=k_u

w(t)=kL^-1{ ∙1}=k 1(t)

h(t)=

W(j ω)=k/(j ω)=-jk/ ω

L(ω)=20lgk-20lg ω

φ(ω)=-π/2

31. Звено запаздывания

Уравнение звена

y(t)=V(t-τ₀); τ₀- время запаздывания

1. v(t)=δ(t); y(t)=w(t)= δ(t-τ₀)

2 . h(t)=

3. W(s)=L{δ(t-τ₀)}= = =e^-sτo

W(s)= e^-sτo- трансцендентная ПФ. Для преобразования её к дробно- рациональному виду используют конечные отрезки её разложений в ряд Паде.

4 . АФХ W(jω)= =cos ωτ₀-jsin(ωτ₀).

R(ω)=1; φ(ω)=- ωτ_{0 .}

L(ω)=20lgl=0; φ(ω)=- ωτ₀

32. Неустойчивое звено 1-го порядка

Уравнение звена

Ty^/(t)-y(t)=kv(t).

Харктеристическое уравнение Ts-1=0 имеет корень s₁=1/T; T>0. Соответственно

W(s)=k/(Ts-1)-ПФ и ИПХ

w (t)=L^-1{ k/(Ts-1)}= =(k/T)e^αt

α=1/T>0 Это звено неустойчивое.

Ty^/(t)-y(t)=0

Решение этого однородного ДУ

y_св(t)=y₀e^αt=> ∞; при t-->∞ , если y₀

h(t)=k(e^αt-1)

W (jω)=k/(j ωT-1)=-k/(1+ ω²T²)- j

φ( ω)€[-π;- π/2] –звено является неминимально-фазовым.

0< ω<∞

АЧХ звена R(ω)=

совпадает с минимально- фазовым апериодическим звеном.

Для min фазовых систем все корни, определенные сомножителями ПФ, имеют отрицательные вещественные части. Для min фазовой системы вид одной частотной характеристики определяет вид другой.

U(ω)V(ω) Они связаны между собой преобразованием Гильберта.

L(ω)φ(ω)

ЛАЧХ неустойчивого звена 1-го порядка совпадает с ЛАЧХ апериодического звена.Фазовые частотные характеристики, определяемые выражением

φ(ω)=-π+arctg ωT,

отличаются от фазовых частотных характеристик апериодического звена.

Анализ систем.

33. Анализ устойчивости.

В основе анализа устойчивости лежат интуитивные предпосылки устойчивости, которые переложены на математику.

Интуитивно устойчивость положения равновесия определяют путем анализа свободного движения системы, возникающего после отклонения системы из точки А равновесия в точкуВ. Следующие графики поясняют эти определения.

Уст. положение y(t)≡0 Неуст. положение y(t)≡0

y(t)≡ . Положение равновесия нейтрально.

В САУ интуитивных определений устойчивости недостаточно. Для этой цели приходится использовать более строгие математические понятия. Рассмотрим их подробнее. Предположим, что система описана ДУ

z^/=G(z,U) (1) z= , z€R_n G= ,G€R_n; U€R_m

U=U(t)- известная векторная функция времени. Поэтому ДУ (1) можно рассматривать в виде

z^/=G₁(z,t) (2)

Предположим, что уравнение (2) имеет решение r(t), t€[0;∞], устойчивость которого надо исследовать.Его рассматривают как невозмущенное решение при r(0)=r₀.

Требуется определить устойчивость этого решения или, другими словами, невозмущенного движения системы. Для определения устойчивости невозмущенного решения требуется исследование всех других решений системы (2), которые получаются при начальных условиях z₀, не равных начальным условиям r₀, при которых получено невозмущенное решение. То-есть исследуются решения z(t), получаемые при z₀=z(t₀)≠r₀

Исследование всех решений системы (2) представляет собой концептуальную проблему, т. к. нелинейные ДУ не имеют общих методов решения. Поэтому применяются различные приемы, которые позволяют косвенно оценить поведение этих решенийя.

1. Второй или прямой метод А. М. Ляпунова.

2. Линеаризованные уравнения- 1-ый метод А. М. Ляпунова.

34. Исследование устойчивости линеаризованных систем

Основные положения прямого метода Ляпунова:

Обозначим общее решение уравнения (2) в виде z(t)=r(t)+x(t).

x(t)- отклонение возмущенного решения z(t) от невозмущенного r(t).

Отклонения x(t) удобно представлять в виде приведенного уравнения.

(3)- приведенное уравнение системы.

M=G(r+x,t)-G₁(r,t) M(0)=0

x(t)≡0- это решение соответствует положению равновесия системы в начале координат.

Если приведенная система находится в начале координат, то исходная система совершает невозмущенное движение. Если положение равновесия в начале координат будет удовлетворять условиям устойчивости, то будет устойчивым и невозмущенное решение системы (2). Для положения равновесия в начале координат или для тривиального решения системы (3) Ляпуновым даны 3 определения:

1. нормы вектора

||x||

l_p=||x||_p, p=1,2,3…

||x||_p=

||x||₂= - длина вектора.

x(t)≡0

Тривиальное решение называется устойчивым, если для любого ε>0 найдется такая величина δ= δ(ε)>0, что ||x₀||< δ, ||x(t)||< ε, t€[0, ).

Все решения, начинаясь в δ- области, не выходят за пределы -трубки.

2. Если тривиальное решение:

асимптотическая устойчивость

Если при асимптотической устойчивости величина δ не ограничена, то систему называют асимптотически устойчивой в целом.

3. Если для любого ε>0 найдется величина δ и хотя бы одно решение x(t)- для которого существует момент t=t₁, при котором ||x(t₁)||=ε, то тривиальное решение системы (3) неустойчиво.

Перейдём к анализу устойчивости по линеаризованным уравнениям. Пусть ДУ

x^/=H(x) (3)

задает приведённую систему, где H(x) можно представить в виде разложения

H(x)=Ax+R(x), (4)

Здесь

A= - матрица Якоби,

R(x)€R_n- остаточный член разложения. Если он удовлетворяет условию

||R(x)||≤||x||^1+α; α>0,

то остаточным членом можно пренебречь и вместо уравнения (3) рассмотреть линеаризированное уравнение

x^/=Ax, (5)

которое и есть уравнение первого приближения.

Общее решение уравнения (5): x(t)=e^Atx₀

Следующие 3 теоремы Ляпунова позволяют связать устойчивость тривиального решения исходного (3) и приведенного (5) уравнений.

det(sI-A)=0, s_i, i=1…n, I=diag1.

Матричный экспоненциал определяется корнями характеристического уравнения s_i=s_i(A)- собственные значения (числа матрицы А)

1. Теорема (об устойчивости). Если все корни s_i,i=1…n характеристического уравнения линеаризованной системы имеют отрицательные вещественные части

Re(s_i=s_i(A))<0, i=1…n,

то тривиальное решение линейного ДУ (5) асимптотически устойчиво в целом, а тривиальное решение исходного нелинейного ДУ (3) асимптотически устойчиво при малых отклонениях (δ-мало).

2. Теорема 2 (о неустойчивости)

Если среди корней характеристического уравнения s_i найдется хотя бы один s_k такой, что Res_k>0, то тривиальные решения ДУ (3) и ДУ (5) неустойчивы.

3. Теорема 3 (критический случай)

Если у характеристического уравнения все корни левые, за исключением одного нулевого или пары чисто мнимых корней, то тривиальное решение системы (5) устойчиво, не асимптотически, а об устойчивости решения системы (3) в этом случае судить нельзя, т. к. устойчивость зависит от членов, отбрасываемых при линеаризации.

Таким образом, если

s_i=s_i(A), Res_i<0 , i=1:n,

то выполняются условия теоремы 1.

Если хотя бы для одного корня

Res s_{k ,} k ,

то выполняются условия теоремы 2.

Если имеется один нулевой или/ и пара чисто мнимых корней

s_l=0; s_k,k+1=±jβ_k,

то -условия теоремы 3.

При исследовании систем, в первую очередь, надо обеспечить условия их асимптотической устойчивости. Это является необходимым условием работоспособности систем. Неустойчивые системы неуправляемы.

Определение устойчивости по местоположению корней характеристического уравнения

det(sI-A)=a₀sⁿ+a₁s^n-1+…+a_n=0

на комплексной плоскости, определённых численно, может привести к весьма существенные погрешностям.

Корни с нулевой вещественной частью, расположенные на мнимой оси, за счет погрешностей вычислений, могут получить вещественную часть, либо положительную, либо отрицательную, или наоборот.

35. Критерии устойчивости.

Критериями устойчивости называют правила, позволяющие оценивать местоположение корней характеристического уравнения без их непосредственного вычисления. Для оценки местоположения эти критерии используют различные характеристики систем, тесно связанные с ее характеристическим уравнением.

Критерии:

1. алгебраические;

2. частотные.

Исходя из модели системы эти критерии можно интерпретировать следующим образом:

Пусть W(s)=

_где

B(s)=b₀s^m+ b₁s^m-1+… +b_{m ;}

­D(s)=d₀sⁿ+ d₁s^n-1+… +d_n.

Уравнение D(s)=0- характеристическое уравнение разомкнутой системы.

Для исследования устойчивости используют корни характеристического уравнения замкнутой системы. Характеристическое уравнение замкнутой системы:

Д(s)=D(s)+B(s)=0 является знаменателем ПФ

Ф(s)= .

Д(s)=a₀sⁿ+ a₁s^n-1+…+a_n

Алгебраические критерии устойчивости:

Критерий Рауса.

1. Критерий Гурвица.

2. Критерий Льенара-Шипара.

Частотные критерии:

1. Критерий Михайлова. Он использует анализ годографа

Д(jω)=Д(s), s=jω, ]

–годографа характеристического многочлена.

2. Критерий Найквиста. Он основан на анализе

W(jω)=W(s), s= jω, ]

–АФХ разомкнутой системы и условия её устойчивости.

3. Логарифмический критерий устойчивости. Это критерий Найквиста, но вместо АФХ используются ЛЧХ разомкнутой системы.

1. Критерий Гурвица:

W(s)=

B(s)=

Из коэффициентов характеристического многочлена

Д(s)=D(s)+B(s)=a₀sⁿ+ a₁s^n-1+…+a_n

_{Если все}

a_i>0, i=1…n.,

то формируется матрица Гурвица

Г=

_{Матрица формируется по правилу:}

По главной диагонали выписываются коэффициенты a_i, начиная с a₁ . Столбцы матрицы вниз от главной диагонали заполняются коэффициентами a_i с убывающими индексами, а вверх – коэффициентами с возрастающими индексами или нулями.

Условие положительности всех коэффициентов многочлена Д(s) является необходимым условием того, чтобы все его корни имели отрицательные вещественные части. Условие называют критерием Стодолы. Если условие не выполняется, то система неустойчива. При выполнении условия вычисляются диагональные миноры матрицы

Δ_i, i=1…n Δ_n=a_n Δ_n-1

Условие

Δ_i>0; i=1…n, где Δ_i- определители Гурвица

является необходимым и достаточным устойчивости замкнутой системы.

Рассмотрим пример.

Пусть n=3. Характеристический многочлен

Д(s)=а₀s³+ а₁s²+ а₂s+ а₃

Матрица

Г=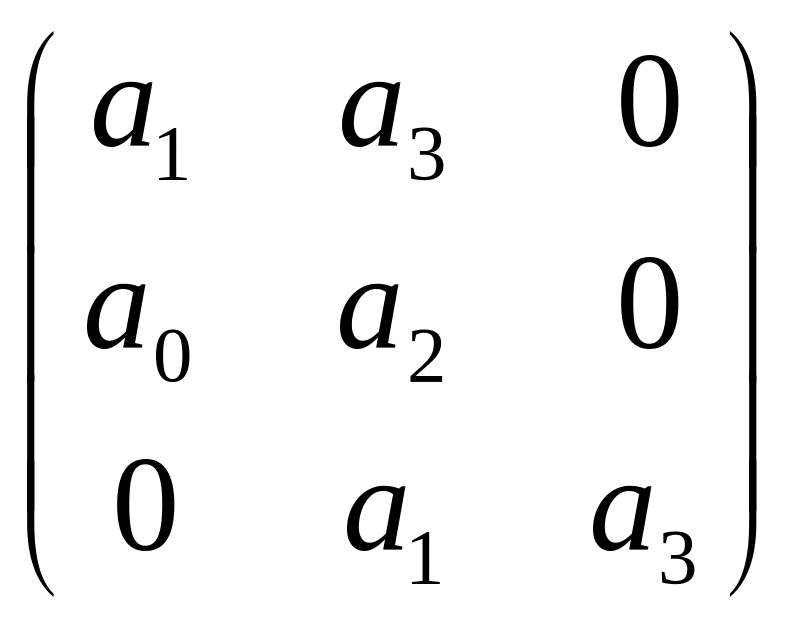

Условие устойчивости:

Δ_i=a₁>0

Δ₂=a₁a₂-a₀a₃>0

Δ₃=a₃∙ Δ₂

a_i>0, i=0…n

При n=4:

Г=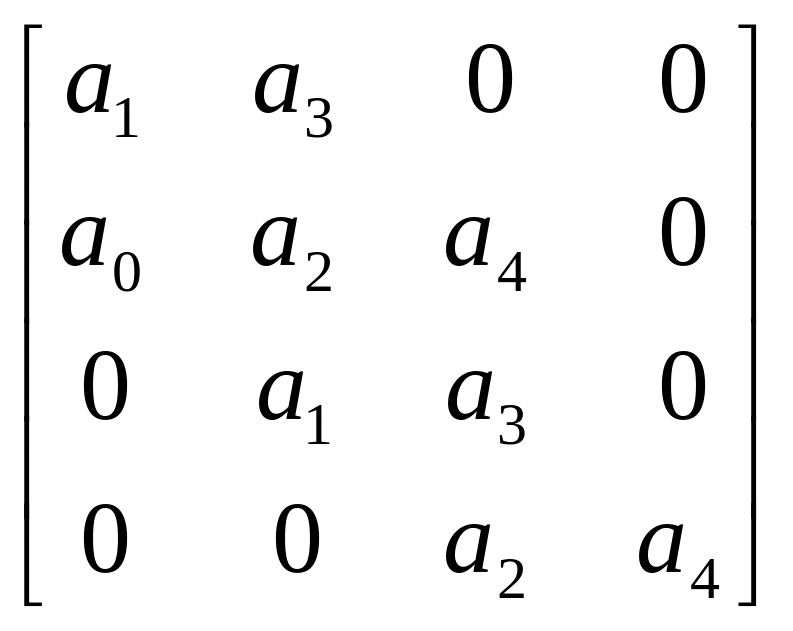

Если изменять параметры системы так, чтобы она из устойчивой превратилась в неустойчивую, то при таком изменении первым обращается в 0 определитель Δ_n-1:

Δ_i>0; Δ_n-1=0; Δ_n-1<0

Критерий Льенара-Шипара:

n- четное- проверяются все нечетные определители Δ_2i-1: i=1…n/2

n- нечетное- проверяются все четные определители Δ_2i: i=1…(2n-1)/2

Определение критического коэффициента усиления разомкнутой системы:

Δ_i>0; i=1…n-2

Δ_n-1=0 при k=k_кр

Все определители до n-2 должны быть положительными, а Δ_n-1=0.

Все эти определители должны давать 2 типа неравенств:

а) k>k_кр, Δ_n-1<0- система неустойчива

k<k_кр, Δ_n-1>0- система устойчива

б) k_кр1 <k<k_кр2, Δ_n-1>0- система устойчива

k ( k_кр1, k_кр2), Δ_n-1<0- система неустойчива.

Пример:

Пусть разомкнутая система имеет вид:

W(s)=

Определим для нее возможные значения k_кр, используя исследования устойчивости, вытекающие из критерия Гурвица. Характеристический многочлен замкнутой системы:

Д(s)=0.25s³+0.8s²+(1+0.1k)s+k=0

Г= Δ₁=0.8>0

Δ₂=0.8(1+0.1k)-0.25k=0

k_кр=0.8/0.17≈5

k>k_кр- неустойчивое; k<k_кр- устойчивое.

ПФ разомкнутой системы включает в себя звенья запаздывания. В этом случае характеристическое уравнение будет иметь не конечное, а бесконечное число корней. Чтобы ограничиться конечным числом корней надо использовать разложение e^So в ряд Падэ, либо использовать критерии, которые не критичны к числу корней характеристического уравнения. Одним из таких критериев является критерий Найквиста.

2. Критерий Найквиста.

Он используетcя для анализа устойчивости систем с единичной ОС, основываясь:

а) на устойчивости разомкнутой системы

б) на виде АФХ W(jω) разомкнутой системы

ПФ замкнутой системы: Ф(s)=

АФХ замкнутой системы: Ф(jω)=

Устойчивость будет определяться нулями функции: 1+W(s)

Пусть

W(s)=

D(s)=d₀sⁿ+d₁s^n-1+…+d_n=d₀(s-s₁)…(s-s_n)

- характеристический многочлен разомкнутой системы.

Характеристический многочлен замкнутой системы:

Д(S)=D(S)+B(S)=a₀ (S-S₁)…(S-S_n)=a₀Sⁿ+ a₁S^n-1+…+a_n

Для анализа устойчивости замкнутой системы рассматривают угол поворота вектора вспомогательной функции f(jω)=1+W(jω) при ω [0;∞)

Угол поворота можно описать как Δargf(jω), ω [0,∞)

Так как f(jω) есть отношение векторов, то ее можно представить:

f(jω)=

Δargf(jω)= ΔargД(jω)- ΔargD(jω)

ω [0,∞); ω [0,∞) ω [0,∞)

1 Случай, когда в характеристическом уравнении разомкнутой системы:

D(s)=d₀(s-λ₁)…(s- λ_n)=0

q- корней λ_i имеет положительные вещественные части, Re λ_i>0.

(n-q) корней λ_i имеют отрицательные вещественные части Re λ_i<0, а в характеристическом уравнении замкнутой системы:

Д(s)=a₀ (s-s₁)…(s-s_n) все n корней части s_i, i=1…n имеют отрицательные вещественные части Res_i<0.

Условие устойчивости этой системы в замкнутом состоянии:

Δargf(jω)= n -[(n-q) +q(- )]=qπ= 2π

Если q=0, то система устойчива, если Δargf(jω)=0

ω [0;∞)

Условие будет выполнено, если годограф f(jω) не охватывает начало координат (кривая 1).

Если годограф охватывает начало координат, то угол оборота не равен 0 и система неустойчива (граф. 2).

От плоскости f(jω) можно перейти к плоскости W(jω), если сместить точку охвата на единицу влево. Точка охвата переходит в точку (-1;j0).

Точка с координатами (-1,j0) называется критической.

Если система устойчива в разомкнутом состоянии q=0 и ее АФХ не охватывает критическую точку, то система в замкнутом состоянии устойчива. Если же охватывает критическую точку, то система в замкнутом состоянии неустойчива. (кривая 2^/).

Таким способом можно определить замкнутую систему для статической системы- когда ν=0.

В общем случае ν=0,1,2,3 и для этих случаев АФХ начинается в бесконечность ν=1: “-j∞”; ν=2: “-∞”; ν=3: “j∞”

Для анализа устойчивости надо исследовать АФХ при малых изменениях ω [-0;0₊]. В этом случае Δarg=-νπ/2

ω [-0;0₊]

Система 1 не охватывает 1, j0, она устойчива. Система 2 охватывает критическую точку, она неустойчива.

Для ν=2

Система 1 устойчива

Система 2- неустойчива

ν=3

Система 1 в замкнутом состоянии устойчива.

Система 2- неустойчива.

Если разомкнуть систему устройства и ее АФХ огибает критическую точку (-1;j0) снизу, то в замкнутом состоянии система устойчива. Если это условие нарушено- АФХ огибает критическую точку сверху, то в замкнутом состоянии система неустойчива.

2) q>0, система не минимально фазовая. В этом в случае надо использовать любое условие, подтверждающее, что Δargf(jω)=qπ

ω [0;∞)

Преимуществом критерия Найквиста является то, что в окончательной формулировке фигурирует лишь устойчивость разомкнутой системы и вид АФХ, т. е. устойчивость систем можно определить по экспериментально снятой АФХ разомкнутой системы безо всякой кК аппроксимации. Это позволяет анализировать устойчивость системы, содержащей звенья запаздывания.

Другим достоинством является то, что он позволяет ввести меру устойчивости. Мера устойчивости выступает, в этом случае, как запасы устойчивости.

36. Запасы устойчивости

Запасы устойчивости x-ют степень удаления АФХ от критической точки при огибании ее снизу и выступают в виде:

1. запас по модулю (амплитуде)

2. запас по фазе .

Эти понятия вытекают из условия существования незатухающих колебаний в системе с ОС.

Пусть на входе разомкнутой системы в виде рассогласования возникает сигнал asinω_Пt. На выходе сигнал a_уsin(ω_Пt-π). По цепи ОС он инвертируется и становится asin(ω_Пt-2π). Если а_y=W(jω_П­)-а=а, то амплитуда будет оставаться неизменной, получим генератор гармонических колебаний. Условие:

В системе, в которой выполняется баланс амплитуд и фаз, АФХ проходит через критическую точку. В этом случае в характеристическом уравнении имеется пара чисто мнимых корней.

Система, имеющая определенный запас устойчивости должна иметь АФХ следующего вида:

1. Для определения запаса устойчивости по фазе проводится окружность единичного радиуса с центом в начале координат. В точке пересечения этой окружности с АФХ частота равна частоте среза:

ω= ω_с R(ω_c)=|W(jω_c)|=1

φ(ω_с) будет определяться углом.

Угол γ=π+φ(ω_с)>0 называется запасом устойчивости по фазе.

2. Запас по модулю определяется исходя из точек АФХ с частотами ω_π2 и ω_π3, ближайшие к критическим. Эти точки являются решением уравнения φ(ω)=-π; ω_π1; ω_π2; ω_π3.

W(j_П2)=-H; H>1

W(j_П3)=-h; h<1

Запас устойчивости по модулю (амплитуде) будет определяться min-ой из точек

min(H;1/h)

Чем ближе эти величины к 1, тем меньше запас устойчивости.

Пример:

W(S)=k/S (1) =90⁰ /2

W(S)= (2)

37. Анализ влияния коэффициента усиления разомкнутой системы на устойчивость замкнутой системы.

1) W(S)=k·W₀(jω)

ν=0

W₀(j0)=1

При увеличении коэффициента усиления система может из устойчивой превратиться в неустойчивую. Это произойдет при k>k_кр.

Такая АФХ называется АФХ I рода.

k<k_кр R(ω_П; k_кр)=1

система устойчива φ(ω_П)=-π

k>k_кр- система неустойчива.

2) АФХ II рода

При увеличении k ω_πi+1 →-1, j0

При уменьшении k ω_πi→-1, j0

Для такой системы может быть несколько k_кр. Условие устойчивости k_крi< k< k_крi+1 - система устойчивая.

3. При любом k охватывают точку системы, которые неустойчивы при любом k>0 называется структурно-неустойчивыми.

Для этих систем φ(ω)<-π

ω [0;∞)

Без введения корректирующих устройств обеспечить устойчивость таких систем нельзя. После коррекции структурно неустойчивой система становится обычной системой. В обычных системах увеличение коэффициента усиления приводит к увеличению запаса устойчивости.

38. Логарифмический критерий устойчивости

Является видоизмененным критерием Найквиста, когда вместо АФХ разомкнутой системы используется ЛЧХ этой системы. Условие устойчивости вытекает из аналогии между АФХ и ЛЧХ.

R(ω_C)=1  L(ω_C)=0

Для рассматриваемой характеристики ω_C< ω_π; R(ω_π)=h<1 L(ω_π)<0

Запас устойчивости по фазе будет дополнением φ(ω_С) до уровня π. Запас устойчивости по амплитуде ΔL=/L(ω_π).

Если изменять коэффициент усиления, то L(ω) будет поступательно подниматься при увеличении k и опускаться при его уменьшении.

k= k_кр, когда ω_С= ω_П- граница устойчивости.

Таким образом, условие устойчивости: ω_С< ω_П

γ, ΔL- запасы устойчивости.

ω_С=ω_П- граница устойчивости: γ=0; ΔL=0

ω_С>ω_П- условие неустойчивости.

Рассматриваемые критерии устойчивости предполагают, что определение характеристик систем не вызовет дополнительных вычислений, что характерно для моделей вх-вых.

Несколько иная ситуация возникает, если для описания системы используется уравнение состояния.

39. Определение устойчивости при описании систем в пространстве состояний.

Предположим, что имеется замкнутая система, которая будет определяться выражением:

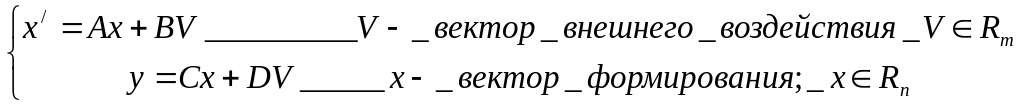
Матрицы А, В, С,D- матрицы соответствующих размеров y R_l. Если использовать критерии Гурвица, то ею непосредственное использование будет связано со следующим вычислением:

1. Нахождение корней характеристического уравнения

det(SI-A)=0 через коэффициент матрицы А.

a₀Sⁿ+a₁S^n-1+…+a_n=0

Вычисление определителя сопрягается, значит погрешность, а корни уравнения степени n>10. Чрезвычайно чувствительны к изменению коэффициентов.

2. Условие устойчивости Δ_i>0, i=1…n-1 не дает однозначного ответа при приближенных вычислениях. Если же анализировать устойчивость по корним характеристического уравнения, то необходимо вычислить det(SI-A)=0 и найти коэффициенты a_i

Вычисление же корней многочлена для уравнения n>3 возможно только численно, используя методы, известные в мат. Анализе.

В настоящее время наметилась тенденция использования матричных критериев устойчивости, которые для определения устойчивости используют непосредственные свойства матрицы А, например, с системе Math Lab оператор.

>>lig(A) S=(S₁,…,S_n)^T возвращает корни характеристического уравнения (составляет значения матрицы А) S_i=S_i(A).

Вычисление этого вектора основано на qr- алгоритме преобразования матрицы. В результате qr- алгоритма матрица А преобразуется в матрицу a₁R₁.

А Q₁R₁

Матрица Q₁ является ортогональной.

Q₁^T=Q^-1

Матрица R₁- верхняя треугольная матрица, у которой отличны от нуля все элементы главной диагонали.

A₂=R₁Q₁ Q₂R₂…

A_n=R_nQ_n

A_n= x- произвольные числа

S_i=(a_ii⁽ⁿ⁾) S_i=a_ii

S_j= S_j,j+1=> λ²(a_ij+a_j,j+1)

det(SI_j-S_i)=

Число итераций100:150, если не приняты меры ускоренной сходимости.

40. Матричный критерий Зубова.

det(SI-A)=0 S_i=S_i(A) i=1…n

Рассмотрим задачу расположения корней характеристического уравнения S_i матрицы А. S- комплексная переменная.

S =α+jω

S= => ρ=

ρ=

Для всех S, принадлежащих левой полуплоскости. α<0.

Для всех S, принадлежащих правой полуплоскости α>0.

Д ля всех S, принадлежащих левой полуплоскости будут соответствовать внутренней части круга радиуса 1. Для S € правой полуплоскости внешней части этого круга.

Рассмотрим изменение характеристического уравнения при такой замене S.

det(SI-A)=det( I-A)=0

det(ρ(I-A)+I+A)=det(ρ (I-A)-(I-A)+2I)=0

det(I-A)^-1; (I-A)^-1- определена

det(ρI-I+2(I-A)^-1)=0

I-2(I-A)^-1­­=B

det(SI-A)=det(ρI-B)=0

Если |S_i(B)|<1, то

S_i=S(B) будут лежать внутри круга единичного радиуса.

ReS_i(A)<0

Если один из S_i(A) будет расположении на мнимой оси, то он будет расположен на границе круга.

1. Если |S_i(B)|<1, то S_i(A)- левые корни.

2. |S_ν(B)|>1, то S_ν(A)- правый

3. |S_k(B)|=1, то S_k(A)=jω_k - чисто мнимый.

Выполнение условий 1, 2, 3 можно проверить и без вычислений с помощью преобразования подобия, получив диагональную матрицу, у которой по диагонали будут корни S_i.

Если рассматривать матрицу B₂=B²

B₄=B²×B²=B⁴

B_2k=B^kB^k

То для устойчивости системы элементы матрицы ||B_2k||→0

k→∞

Если же какой-либо элемент матрицы при к→∞ возрастает, это свидетельствует о том, что матрица А имеет правые корни и система неустойчива.

Если какие-либо элементы матрицы не возрастают и не убывают, то матрица А имеет чисто мнимые корни характеристического уравнения. Таким образом, алгоритм вычисления по Зубову:

1) (I-A)^-1

2) B=I-2(I-A)^-1

3) B₂=B₂×B₂

B_2k=B_k×B_k

Затем проверяется стремление к 0 элементов этих матриц.

Кроме критерия Зубова в некоторых случаях анализ устойчивости проводится на основе матричного уравнения Ляпунова.

Анализ точности в установившихся режимах.

41. Общие сведения об анализе точности

Устойчивость системы- это необходимое условие работоспособности. Для устойчивости систем возникает требование к точности обработки технических или иных входных воздействий. Наиболее удобно точность рассматривать при использовании моделей вх-вых систем.

Вынужденные движения в системе, т. е. движение системы обусловлено входным воздействием и возмущением F(S), будет описано в операторной

форме следующим образом:

Y(S)=Ф(S)∙V(S)+Ф_f(S) ∙F(S)

Если считать ошибкой разность:

E(S)=V(S)-Y(S)=1-Ф(S)V(S) - Ф_f(S)F(S)

E_v(S) -E_F(S)

Полная ошибка воспроизведения входного сигнала:

E(S)=E_v(S)+E_F(S)

e_v(t)- ошибка воспроизведения входного воздействия.

e_f (t)- ошибка по возмущению.

Эти ошибки зависят как от свойств системы Ф_ε(S)=1-Ф(S) и от передаточной функции по возмущению Ф_f(S) (Ф_ε(S)- ПФ по ошибке), так и от самих сигналов.

Принято оценивать ошибки при типовых внешних сигналах.

Ошибки E_V(S) и E_f(S) рассматривают отдельно. В качестве типовых воздействий используется:

1. полиномиальные воздействия, при которых

V(t)= ; i=0,1,2,…

Частный случай: i=0

V₀(t)=a₀∙1(t)

i=1; V₁(t)=a₀1(t)

i=2;

2. Медленно меняющиеся сигналы:

V(t)=

3. Гармонические сигналы.

V(t)=Asinωt, ω [0,∞)

4. Сигналы с ограниченной скоростью и ограниченным ускорением:

max|V^/(t)|≤υ_m, где υ_m- max скорость.

max|V^//(t)|≤a_m, где a_m- max ускорение.

42. Полиномиальные сигналы.

Сигналы в виде однородных полиномов.

V(t)= ; r=0,1,2…-порядок

L{ }= , r=0,1,2,…

W(S)= , K- коэффициент усиления

-порядок астатизма

W(S)=1 при S=0

Найдем изображение ошибки при действии на вход системы полиномиального сигнала.

E(S)=Ф (S)V(S)=

При анализе точности интересуются установившимся значением ошибки Е_уст(t)

E_ycт= Е(t)

Для нахождения Е_уст используют теорему о конечных значениях:

Е(t)= S Е(S)

Е_уст=

Рассмотрим Е_уст при различных r в системах с различными ν

1. r =0 V(t)=a₀1(t) V(S)= Ошибки, возникающие в системе называются статическими (или ошибка по положению) Е_уст =Е_ст

а) ν =0 статическая система Е_ст=

б) ν =1,2… астатическая система Е_ст=0

2. r=1; V(t)=a₁t ; t [0;∞)

V (S)= Е_уст =E_ск ошибка по скорости

а) ν =0 статическая система Е_ск=∞

б ) ν =1 система I порядка астатизма Е_ск=

в) ν =2,3… Е_ск=0

Нулевая ошибка, говорящая о методической составляющей. Имеет место ошибка, которая называется инструментальной.

3) r =2

V(t)= квадратическая парабола

V (S)= Е_уст= Е_уск ошибка по ускорению. Сигнал меняется с постоянным ускорением.

а) ν =0;1 Е_уск=∞

б ) ν =2 Е_уск=

в) ν=3… таких систем практически не бывает Е_уск=0.

1.Если ν=r, то наблюдается ненулевые установившиеся ошибки:

E_ycm

2.ν>r Е_уст=0

3.ν<r E_уст=∞.

43. Особенности анализа ошибки по возмущению.

f(t)= , r=0,1,2

Для анализа Е_{f уст}= Е_f (t)

Используется теорема о конечном значении.

Е_{f уст}= Е_f (t)= S Е_f (S)

ν₁

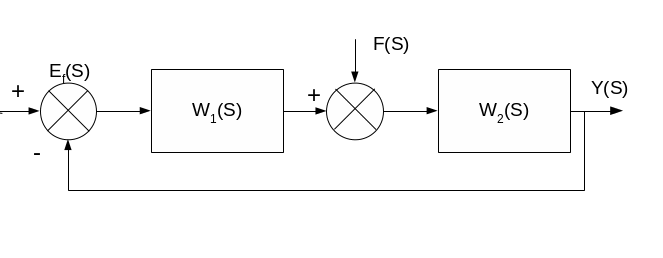
y_{f уст}= y_f (t)

Е_{f уст} и у_{f уст} совпадают с точностью до знака

W₁(S)= ; W₂(S)=

Y_f(S)=

Сравним это изображение с изображением установившейся ошибки:

₁ –порядок астатический по возмущению

= ₁ + ₂ – порядок астатический по управлению.

Медленно меняющиеся сигналы.

44. Коэффициенты ошибок.

Медленно меняющиеся сигналы – такие сигналы, у которых для любого момента времени имеется ограниченное число ограниченных производных.

Пример:V(t)=

При анализе точности воспроизведения такого сигнала вновь исходя из анализа по Лапласу ошибки:

E(S)=Ф_Е(S)V(S), где Ф_Е(S) - передаточная функция по ошибке.

Ошибка возникает при больших t, когда в системе заканчиваются переходные процессы, вызванные этим воздействием, поданным на вход.

Поведение ошибок зависит от E(S), когда S- мало

Ф_Е(S)=C₀+С₁S+…+C_kS^k+…

C_i= Ф⁽ⁱ⁾(0)

Ряд сходится, если все С_i ограничены

E(S)= C₀V(S)+ C₁SV(S)+…+ C_kS^kV(S)+…

Возьмём L^-1; получим

Е_уст(t)=С₀V(t)+C₁ (t)+…+C_kV^(k)(t)

C_i= коэффициенты ошибок i=0,1,2…

Величина С_i определяется порядком астатизма и коэффициентом усиления разомкнутой системы

r=0, V(t)=a₀1(t)

E_уст(t)=С₀а₀1(t)=

1. =0; C₀=

2. =1,2…; C₀=0

C_0- коэффициент статической ошибки. Для статической системы C₀=0.

Если к=1, то V(t)=a₀1(t)+а₁t

E_уст(t)=С₀(a₀1(t)+а₁t)+С₁а₁

=0; C₀≠0, E_уст(t)→ ∞ при t→∞

=1; C₀=0 E_уст(t)= C₁= Иногда коэффициенты ошибок связывают с моментами ИПХ замкнутой системы. Рассмотрим эту связь:

y(t)=

V(t) медленно меняющийся сигнал.

Представим как ряд Тейлора.

V(t-τ)=V(t)+V`_τ(t)(-τ)+ V``_τ(t)(-τ)²+…+ V^(k)_τ(t)(-τ)^k

Подставим это разложение в интеграл свертки:

Е(t)=V(t)-y(t)=V(t)- V(t) +

μ_i= момент порядка i

E(t)=(1-μ₀)V(t)+

C₀=1- μ₀

C_i=(-1)ⁱ μ_i

Для астатических систем =1,2…; C₀=0; μ₀= =1

Порядок астатических систем определяет число первых коэффициентов ошибок, равных 0

=0 C₀≠0

=1 C₀=0; C₁=1/k

=2 C₀=C₁=0; C₂=1/k

45. Анализ точности при гармонических сигналах

V(t)=a_msin(w₀t) Для устойчивых систем

E_уст(t)= а_Emsin(w₀t+φ_E)

Величина ошибки оценивается по величине а_{Em (}по амплитуде)

Из определения АФХ по ошибке а_Em

Для систем с единичной ОС:

a_{Em= ; при} >>1

46. Анализ точности при сигналах, ограниченных по скорости и ускорению.

max максимальная скорость сигнала V(t)

max максимальное его ускорение.

V_эк(t)=А_экsin(Ω_экt)

А_экΩ_эк Ω_эк

А_экΩ²_эк

E_m

47. Пути повышения точности системы в установившихся режимах

1. Понятие об инвариантности систем.

Система называется инвариантной к внешнему воздействию, если она воспроизводит этот сигнал с нулевой ошибкой, как в переходном, так и в установившемся режиме. Требование равенства нулю ошибки означает, что система должна точно копировать входной сигнал на выходе и иметь нулевую реакцию на возмущение.

Передаточная функция: Ф(S)=1

Передаточная функция по возмущению: Ф_f(S)=0

Р ассмотрим возможность реализации условия инвариантности в рамках системы с единичной ОС

Ф(S)=

В некоторых случаях в систему вводят дополнительные связи по управлению для увеличения точности. W(S)= W₁(S) W₂(S)

Ф(S)=

W₂(S)( W₁(S)+φ(S))=1+ W₁(S) W₂(S), это возможно, когда:

W₂(S) φ(S)=1 или периодическая функция дополнительные связи:

W₂ отражает наиболее инерционные элементы системы. Их передаточная функция имеет порядок знаменателя больше порядка числителя.

Нельзя найти физическую реализацию φ(S), которая обеспечит абсолютную инвариантность системы на входное воздействие.

Рассмотрим инвариантность системы при действии возмущения:

W₂(S)=0

Рассмотрим дополнительную связь: - передаточная функция дополнительной связи

F(S) измеряется с помощью какого-либо датчика

= W₁(S)=k

Если реализовать такую возможность, то получим систему комбинированного регулирования.

В общем случае реализовать комбинированную систему невозможно

Реализуем частичную инвариантность (до Е)

Частичная инвариантность эквивалентна повышению порядка астатизма системы по входу и возмущению. Покажем, что с помощью выбора φ(S) можно статическую систему преобразуют в астатическую II порядка без использования интегральных звеньев.

Эта система статическая.

Ф_Е(S)=

1- φ(S)W₂(S)

W₂(S)=

(e_n-C_n1)d₀=1

(e_n-1-C_n1-1)d+(e_n-C_n)d₁=0

W₂(S)=^C(S)/_G(S)

Ф(S)=

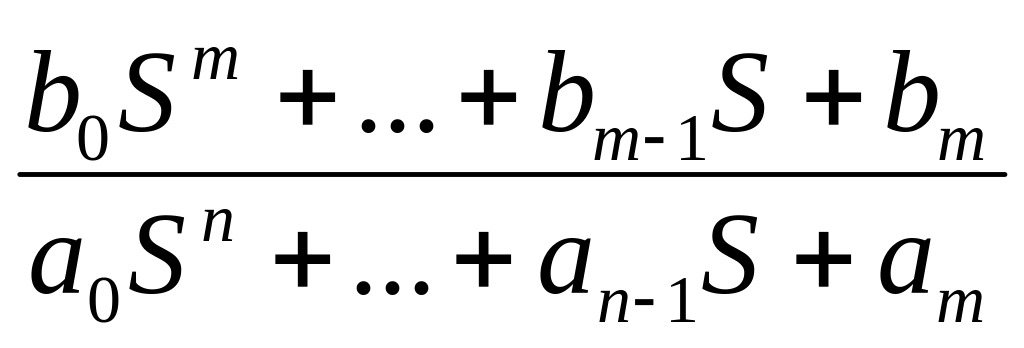
b_m=a=n; b_m-1=a_n-1

Такого же эффекта увеличения порядка астатизма можно добиться, если в системе 2 интегральных звена, но при этом система станет неустойчивой, так как изменяется характеристическое уравнение. Введение дополнительных связей не меняет характера уравнения и не влияет на устойчивость.

2 . Повышение порядка астатизма включением интегрального звена.

W(S)= T=

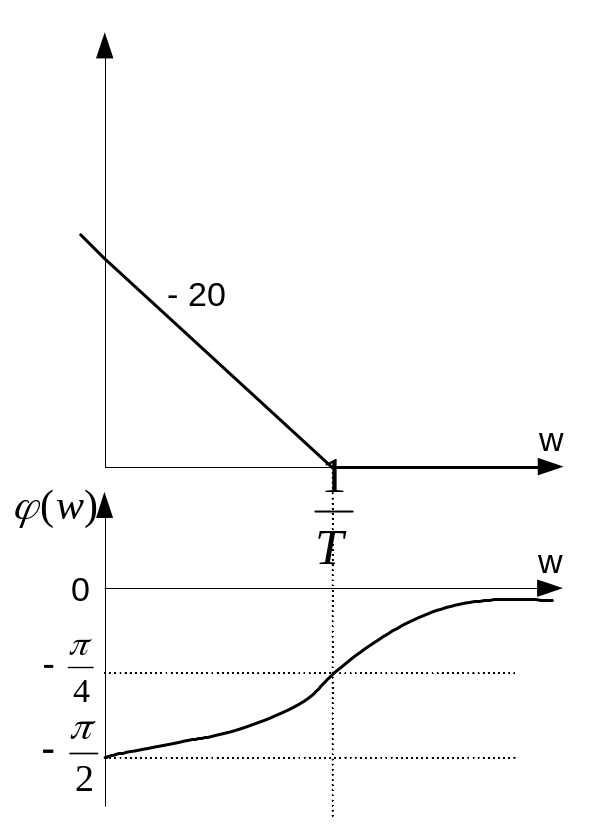
φ(w)=

K_П>>K_И Т>>1 w >1/T

ЛЧХ системы не изменяется.

Дальнейшее увеличение точности обеспечивается за счет увеличения коэффициента усиления системы.

3. Масштабирование.

А. Масштабирование в прямой цепи

W(S)=KW₀(S)

Ф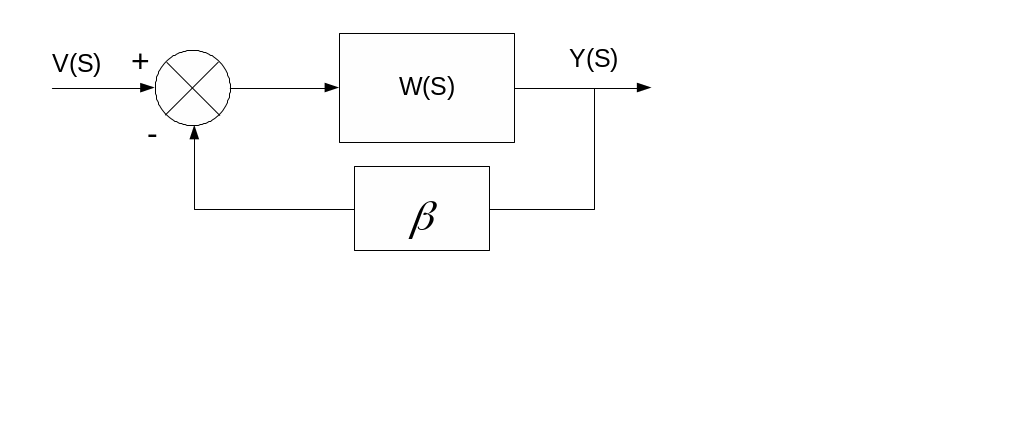 (S)= Kз=Ф(0)= mK=1+K; m=

В. Масштабирование в цепи ОС

Ф(0)=

Практически статических систем нет, так как простым масштабированием им даются свойства систем с астатизмом I-го порядка.

48. Анализ качества переходных процессов

1. Понятие о качестве переходных процессов.

Y(S)=Ф(S)V(S)+ Ф_f(S)F(S) -изображение вынужденной составляющей.

Если начальные условия не равны 0, то

Y(S)=Ф(S)V(S)+ Ф_f(S)V(S)+Y(S,Y₀) ,где

В процессе работы различают ненулевые начальные условия, различные входные сигналы, которых может быть несчетное множество. Качество переходных процессов в системе оценивается по виду её переходной характеристики.

Для анализа качества переходной характеристики рассмотрим входной сигнал.

1)V(t)=1(t)

V(S)=

F(t)=0 F(S)=0

Получили выражение переходной характеристики по входу:

Y(S)=H(S)=Ф(S)

h(t)=

S_i –корни характеристического уравнения.

Д(S)=0, i=

h(t)=

Переходная характеристика является либо типовым, либо неблагоприятным режимом работы системы, в котором проявляются динамические свойства системы

2) V(t)=0

F(t)= 1(t)

H_f(S)=Ф_f(S) изображение переходной характеристики по возмущению

h_f(t)=L^-1{H_f(S)}

49. Показатели качества переходного процесса, определяемые по переходной характеристике.

А) качественные

Б) количественные

h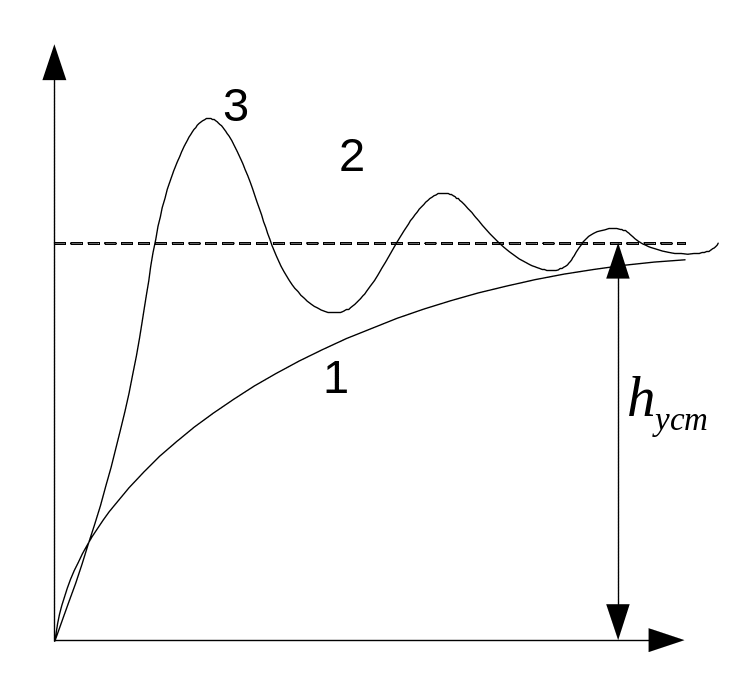 (t)=h_ycm при t→∞(t≥t_p)

1- монотонная

2- слабоколебательная

3- сильноколебательная

Качественные показатели не позволяют объективно оценивать переходной процесс, особенно на границе между определениями.

Чтобы избежать субъективизм используют количественные показатели.

1. Перерегулирование σ

2. Время регулирования t_p:(h(t)-h_ycm) t≥t_p

от h_ycm

Эти два показателя являются основными, они задаются на разработку любой САР

σ≤ σ_задан; t_p≤ t_{p задан}

3. Время установления t_y

4. t_m время первого максимума

5. æ-число колебаний за время t_p

Чтобы оценивать качество системы разрабатывают многочисленные группы методов анализа качества переходных процессов. Их можно разбить на 2 больших группы:

• Прямые методы

• Косвенные методы.

Прямые методы предполагают определение выделенных показателей качества непосредственно по кривой h(t). К прямым относят методы, позволяющие построить график h(t) или найти для него математическое выражение. Они используются как доказательство, что разрабатываемая система имеет показатели качества не хуже заданных.

Косвенные методы менее трудоёмкие, чем прямые, и позволяют оперативно оценивать выделенные показатели качества. На этапе выбора структуры и параметров системы. Далее рассмотрим эти методы подробнее.

50. Прямые методы.

Прямые методы – методы решения дифференциальных уравнений системы.

W(S)=

Ф(S)=

Д(p)h(t)=B(p)1(t)

B(p)=b₀p+b₁

t=0_ h(0)=h`(0_)=0

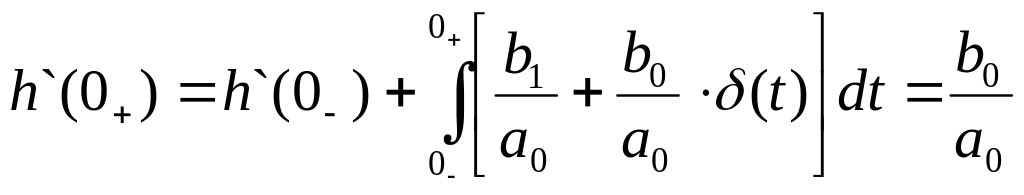
Среди этих методов выделяют:

1. Теорема разложения Хевисайда

Характеристическое уравнение замкнутой системы Д(S)=0

S_i=S_i(Д); i=

h(t)= , где ;

2. Классические методы решения дифференциальных уравнений;

3. Использование теоремы разложения;

4. Методы численного решения дифференциальных уравнений (методы моделирования);

5. MATLAB, VISSIM, Mathcad. Используется численное моделирование дифференциальных уравнений

51. Косвенные методы

Косвенные методы предполагают для оценки показателей качества использование различных характеристических систем, связанных с её переходной характеристикой. Все эти методы можно разбить на две группы:

• Корневые

• Частотные

Корневые предполагают использование корней характеристических уравнений. Они могут выступать в виде нуль-польных портретов системы(комплексная плоскость, на которой отмечены все нули полюсы передаточной функции замкнутой системы) или в виде корневых годографов (траектории, описывающие изменение значения корней характеристического уравнения при изменении одного или нескольких его параметров, например, коэффициента усиления разомкнутой системы.)

Частотные методы используют различные частотные характеристики, например, Р(ω)-вещественная частичная характеристика.

h(t)=

M(ω)-АЧХ замкнутой системы

W(jω)-

W^-1(jω)- обратная АФХ разомкнутой системы

L(ω)-ЛЧХ разомкнутой системы

52. Оценка показателей качества по корням

И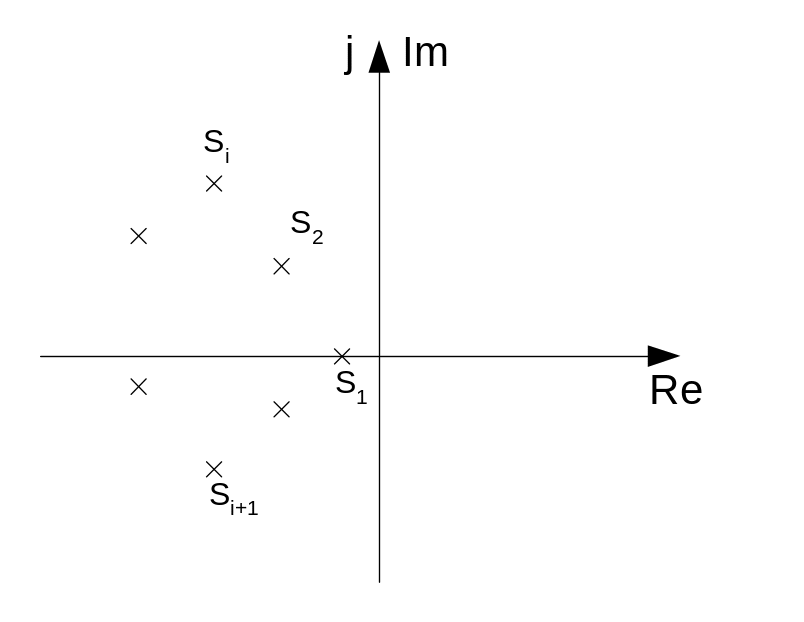 меется комплексная плоскость с точками, соответствующим корням.

|-α|=δ=α степень устойчивости

Α позволяет оценить практическое время переходного процесса t_p

S₁→C₁e^{α t}=h₁(t)

h(t)=

переходной процесс закончен, если αt_p≥3 t_p≥

Е сли t_p≤ t_{p задан} , то ,

Е сли S₁и S₂ мнимые корни, то их величина будет определять δ

Все составляющие h_i(t) будут имеет ограниченную колебательность, если величины β_i ограничены в соответствии с α_i

За какой-то период колебаний h_i(t) затухнет.

α_i2π≥3β β_i≤⅔πα

5 3. Оценка показателей качества по ачх замкнутой системы.

Ф(jw)= =M(w)e^jθ(w)

M(w) – АЧХ замкнутой системы

Типовое значение АЧХ иллюстрируется следующим графиком:

w _p – резонанасная частота

М(w_p)=

M(0)= w_c – частота среза

L(w_п) – частота положительности, связанная с w_c

w_п =(0,6÷0,8)w_c

Величина М_мах показывает склонность системы к автоколебанию М_мах→∞

Величина M(w) полностью определяется значениями АФХ разомкнутой системы.

W(jw)=ν (w)+jV(w). Определим линии равных значений М

М(w)=

ν²+V²=M²[(1+ν)²+V²]

ν²(1 -M²)-2 M² ν+(1 -M²)М²=М²

ν²-2 ν+ V²=

(ν+ )²+V²= (1 )

С= ; R=

(ν +C)²+V²=R²

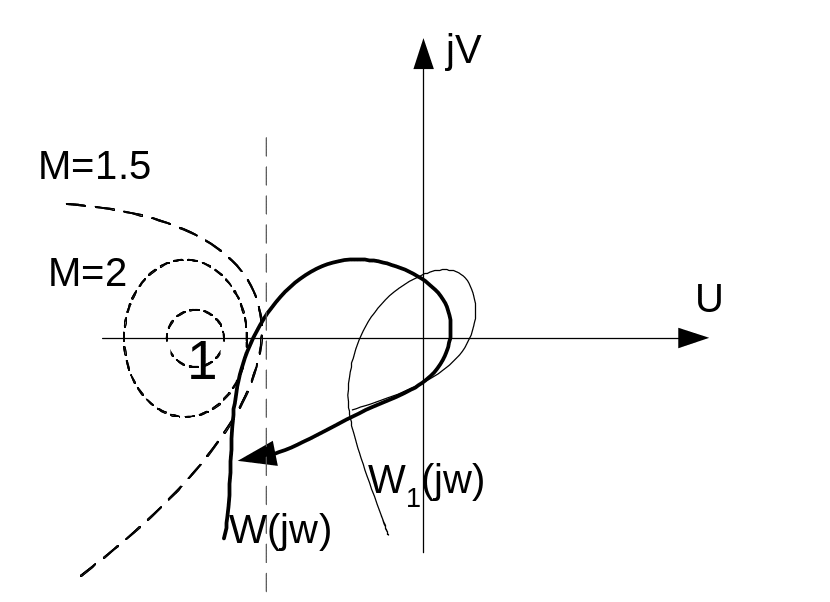
М_мах→∞

М_мах≤1.1÷1.5

σ≤60%

М_мах=1; σ=0

54. Оценка показателей качества по лачх разомкнутой системы.

Типовая ЛАЧХ, L(w), (L(w),φ(w))

Р ассмотрим минимальные фазовые системы, для которой вид одной характеристики определяет другую.

1. СЧ участок (среднечастотный) w<w₂,w₃c -20дб/дек

2. НЧ участок w<w₁ -20 дб/дек ν=1 – первый порядок астатизма

3. Участок сопряжения НЧ со СЧ участком задается соотношением 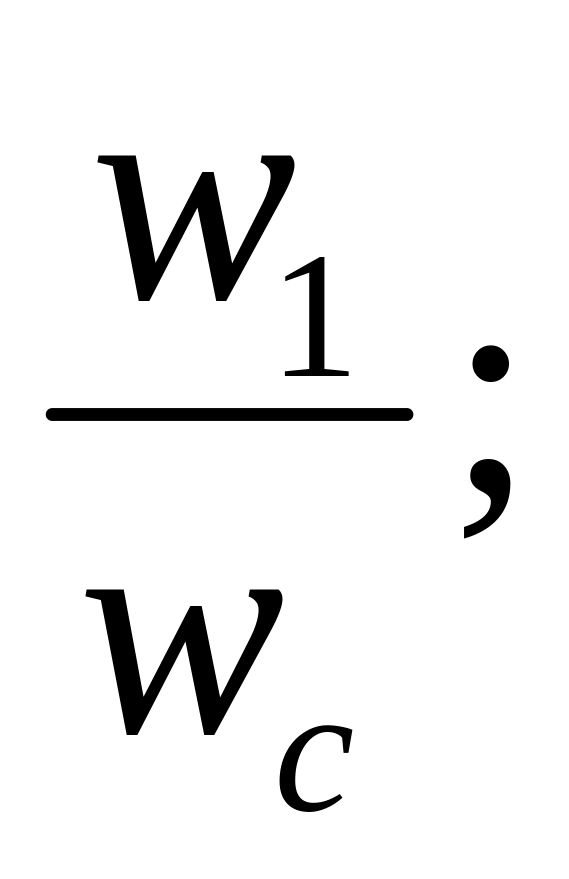, имеет наклон - 20 mдб/дек, m=1,2,3…

Быстродействие и время регулирования.

1. tg ; t= k=1,2,3… коэффициент, определяемый исходя из перерегулирования (σ)

2. Перерегулирование зависит от длины среднечастотного участка w₂÷w₃- 20дб/дек. При длине < 2 декад появляется погрешность перерегулирования, зависящая от и . Если w₃-w₂≈2 декадам, то σ =0

Низкочастотный участок w≤w₁ не сказывается на качестве переходного процесса, но определяет точность в установившемся режиме.

-20дб/дек ν=1 система астатическая первого порядка

-40дб/дек ν=2

0 ν=0

Высокочастотный участок w>w₄ практически не оказывает влияния на время переходного процесса L(w)<-25дб/дек

55. Интегральные оценки качества

Эти оценки позволяют связать в единый показатель точность в установившемся режиме и качество переходного процесса. Пусть имеется замкнутая система

V(t)=1(t) y(t)=h(t)

x(t)=y_ycm-y(t)= h_ycm-h(t) h_ycm=Ф(0)

y_ycm установившееся значение переходной характеристики

Интегральной оценкой качества называются различные интегралы от функции x(t). Интегральная оценка будет определять некоторую площадь от кривой.

1. Простейшей оценкой является линейная оценка .

I₁= соответствует площади подл кривой.

Если x(t) монотонная функция, не меняющая знак, то этот интеграл будет состоятельной оценкой качества переходного процесса.

Оценка I₁ просто считается.

Пусть х(S)= положим , что S=0, то I₁= x(0) x(S)=(Ф(0)-Ф(S))

Если представит Ф(S) как отношение двух многочленов

Х(S)=

Недостатками оценки является то, что при колебательном S(t) оценка I₁становится несостоятельной, так как из её малости не следует малость модуля площади под кривой x(t). Состоятельной оценкой была бы следующая оценка:

I₁₁= Она состоятельна как для монотонных, так и для колебательных процессов, но связать её с передаточной функцией с помощью простых выражений не удается.

2. Квадратическая оценка

I₂= Эта оценка подчеркивает большие оценки. Оценка является состоятельной для колебательных процессов.

Е ё вычисление в конечном итоге сводится к интегралу Релея.

I₂= = Интеграл Релея приводится в приложениях. Рассмотрим связь I₂ с параметром передаточной функции.

x(jw)=[Ф(0)-Ф(jw)]

Рассмотрим случай астатичесой системы ν=1,2… Ф(0)=1; для них Ф(0)-Ф(jw)-Ф_с(jw)

I₂ для астатических систем можно посчитать следующим образом:

I₂=

Как I₁, так и I₂ достаточно вычислить в общем виде через параметры передаточной функции. При анализе систем часть параметров является неизменяемыми, заданными, а часть их можно менять.

Для простоты предположим, что передаточная функция имеет 2 параметра α и β, тогда

I=I(α, β) α [ α_min ;α_max] β [ β _min ;β _max]

Обычно знак параметров выбирают так, чтобы I→min h(t) →h наиболее близко к идеальному переходному процессу. Для нахождения минимумов можно взять условие экстремумов:

Если α* и β* внутренние точки интервала допустимого α_доп β_доп, тогда можно найти I₂(α*, β*), если нет , то нужно воспользоваться граничным значением. Рассмотрим процедуру минимизации оценок параметров синтезом. Она позволяет при известной структуре системы выбрать наилучшее значение параметров с учетом ограничений. Практика применения такого метода определяет оптимальных параметров при минимизации I₂ показала, что переходные процессы при оптимальных параметрах могут получаться слишком колебательными. В этом случае возникает задача ограничить колебательность за изменения оценки I₂. В результате такой модуляции получается оценка I₂₁

I₂₁=

В оценку I₂₁ входит также интервал, характеризующий скорость изменения колебательного процесса. Поэтому с учётом члена Т (t) будет минимизация и скорость колебательного процесса. В этом случае оптимум процесса будет другой. Найдем оптимум процесса, соответствующий I₂ →min

I₂₁=

Условие минимума будет следующим

T однородное ДУ. Его решение х*(t)=x0e-t/T , где T - постоянная времени, которая выбирается исходя из определённых соображений.

Монотонному процессу х(t) будет соответствовать монотонный процесс h*(t)

h*(t)=h_ycm(1-e-t/T) h*- переходная характеристика апериодического звена.

Вычисление интеграла I₂ несколько более сложное. Для получения более гладких переходных процессов в оценку I₂₁ включают члены, содержащие вторую и более высокие производные.

Чувствительность систем.

56. Функции чувствительности.

Предположим, что система описана ДУ:

x(t) – координаты состояний

- вектор изменения параметров

- номинальные значения параметров, которые в процессе работы системы могут принимать различные значения

Δα₁,…,Δα_m – отклонения

При номинальных параметрах:

При измененных параметрах:

- возмущенное решение

- невозмущенное решение при номинальных значениях

, где R₂(Δα_j²) – остаточный член,

Функция чувствительности, определяемая при номинальных значениях параметров: , где U_{i j} , образует матрицу n*m

Таким образом, если отклонения Δα параметров невелики, то остаточным членом можно пренебречь:

,

Находить функции чувствительности в виде производных обычно затруднительно.

При больших n, для изучения функции чувствительности, их задают решением специальных ДУ, которые называют ДУ чувствительности:

Продифференцируем левую и правую части уравнений:

, ,

Уравнения чувствительности для нелинейных систем:

, ,

Если исходная система описывается линейным ДУ, то система все равно получается нелинейной. Для решения систем используются только численные методы и методы моделирования.

Коррекция систем.

57. Общие сведения о коррекции

Систему, составленную из необходимых элементов, и имеющую коэффициент усиления в разомкнутой системе k = k_тр и порядок астатизма υ = υ_тр, называют нескорректированной. Эта система, имея требуемую точность обработки установленного сигнала, не обладает требуемым показателем качества переходных процессов, т.е. просто неустойчива. Возникает задача коррекции нескорректированных систем. Цель коррекции – придание системе таких свойств, при которых она обладает требуемым показателем качества переходных процессов. Коррекция осуществляется с помощью дополнительной коррекции устройств. При описании системы вход – выход корректирующие устройства могут включаться в систему либо последовательно в цепь прямой передачи сигнала, либо параллельно, охватывая один или несколько функционально необходимых элементов (цепь МОС).

При описании системы коррекция осуществляется в виде обратных связей по состоянию.

58. Последовательная коррекция

1.Пусть задана нескорректированная система

W_нс(s) – передаточная функция нескорректированной системы

а)

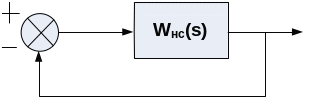
б)

При включении системы – корректир. сист.

W_ск(s) = W_ку(s) *W_нс(s)

Наиболее удобно последовательную коррекцию изучать с помощью ЛЧХ:

L_ск(ω) = L_ку(ω) + L_нс(ω)

φ_ск(ω) = φ_ку(ω) + φ_нс(ω)

Коррекцию аналоговых систем удобно осуществлять с помощью типовых RC-соединений:

1. Дифференциальный контур.

2. Интегрирующий контур.

3. Интегро-дифференцирующий контур

Рассмотрим возможности коррекции каждым из контуров:

дифференциальный контур

W_дк(s) = R₂/ =

= ; W_дк(s) =

<1; T = R₁*c

ЛЧХ: arctg(ωT) – arctg(αωT)

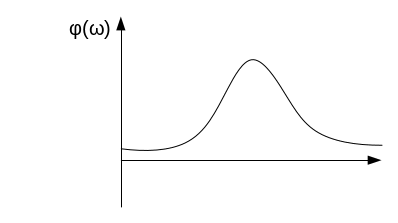
Уменьшение коэффициента усиления недопустимо, т. к. к = к_треб. При включении дифференциального контура необходимо увеличить коэффициента усиления каскада усилителей так, чтобы общий коэффициент усиления остался неизменным. Сигнал U₁ будет содержать шумовые высокочастотные составляющие. Величину α ограничивают, чтобы сигнал не затерялся в шумах (α 0.2; ). Увеличение ω_с, φ(ω) происходит за счет положительного φ_дк (ω).

Правильно подобранный контур позволяет увеличить быстродействие, но уменьшает помехоустойчивость.

и нтегрирующий контур:

W(s) = = ; T₁=R₁*С; T₂=(R₁+R₂)*С; T₁<T₂ ЛЧХ:

φ(ω) = -arctg(ωT₂) + arctg(ωT₁)

Контур пропускает низкочастотные составляющие, ослабляет высокочастотные составляющие входного сигнала, в том числе помехи, поэтому контур высоко помехозащищен. Запас по фазе увеличивается за счет уменьшения ω_с, уменьшается быстродействие системы, что ведет к увеличению времени регулирования.

интегро-дифференцирующий контур:

W(s) =

T₁ = R₁*C₁; T₂ = R₂*C₂; T₃*T₄ = T₁*T₂

T₄ > T₁ > T₂ > T₃

Правильно подобранный интегро-дифференцирующий контур позволяет уменьшить коэффициент передачи в области средних частот, почти не меняя ω_с, и обеспечивает положительный сдвиг по фазе в области частоты среза. Можно воспользоваться 2-мя корректирующими условиями.

где РУ – развязывающее устройство,

R_вх - велико

59. Параллельная коррекция

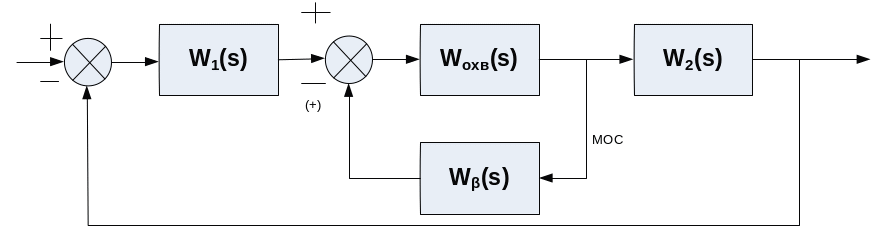
W_охв (s) – ПФ элементов, охваченных МОС

W_β (s) –ПФ параллельного КУ

W_ск(s) = W1(s) =

W_{к экв}(s) =

Последовательному КУ будет соответствовать некоторое параллельное КУ и наоборот.

В зависимости от свойств W_β (s), МОС делят на жесткие и гибкие :

ЖОС: W_β (0) 0

ГОС: W_β (0) = 0

Примеры:

1. Охват усилителя с большим К_охв:

W_куэ = ,

W_куэ = , W_β (s) = T₁S +1

2. Охват апериодического звена ЖОС:

W _э(s) = =

Т₁ = ; К₁ =

Уменьшение коэффициента усиления

нетрудно скомпенсировать за счет усилителя.

3. О хват последовательно соединенных апериодического и интегрирующего звеньев ЖОС:

W_э = =

Соединение стало статическим.

4. Охват апериодического и интегрирующего звеньев ГОС:

W_э =

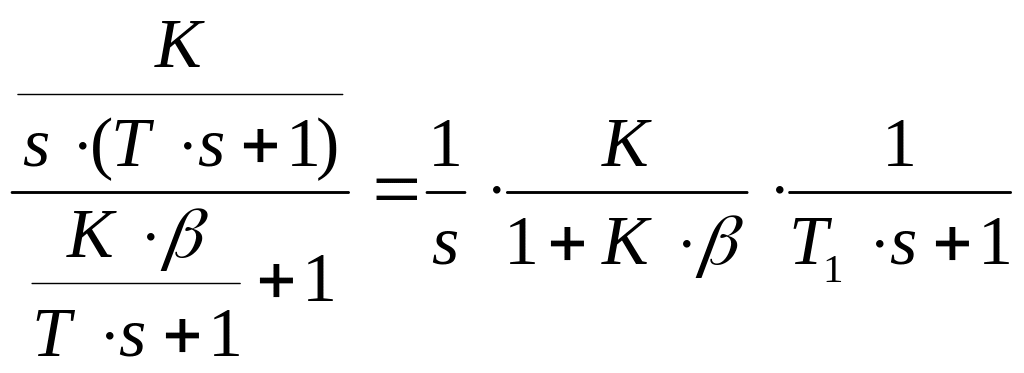
T₁ =

5. Оценка коррекции по ЛЧХ:

Сложные выражения: W_охв (s) и W_ку (s) W_кэ (s)

W_ск(s) =

L_ск(ω) = L_нс(ω) – 20 lg

Ľ₂(ω) = 20 lg

Ľ₂(ω) =

По рассмотренной методике решают задачи разработки систем с заданными свойствами, задачи синтеза. В общем случае задача синтеза сложна и не получила своего окончательного решения для линейных стационарных систем. Поэтому синтез осуществляется не как нахождение некоторой наилучшей системы, а как реализация желаемой системы. После выбора этой системы решается задача коррекции нескорректируемой системы с тем, чтобы приблизить скорректированную систему к желаемой. При этом в самих системах для коррекции может использоваться обратная связь по состоянию.

60. О модальном регулировании

x` = Ах(t) + BU(t) x(t) R_n; U(t) R_m

y(t) = Cx(t) (1) y(t) R_e

Для управления этой системой можно использовать сигнал U(t) = V(t) – F*x(t) (2)

1. – уравнение разомкнутой системы

2. – принимает вид для замкнутой системы

V(t) – задающий сигнал, F*x(t) – сигнал ОС

(3)

A A_R = A – BF – системная матрица замкнутой системы

rank R =

если (А, В) – полностью управляема, то F – регулятор

det (sI - A_R) = 0

S_i*(A_R) – наперед заданные корни

Модальное регулирование – управление расположением мод замкнутой системы

F – модальный регулятор

Это управление удобно реализовать, если вектор состояния x(t) имеет измер. координаты состояния. Реализация модального управления наводит на непреодолимые затруднения. Вместо модального управления, матрицу F выбирают как стабилизирующую управлением.

det (sI - A_R) = 0

S_i (A_R) : I = , ReS_i(A_R) устойчивость с запасом

δ – степень устойчивости

Дискретные системы

61. Общие сведения о дискретных системах

Система называется дискретной, если хотя бы один из сигналов имеет дискретную форму (импульсная или цифровая). При автоматическом управлении все объекты управления являются аналоговыми, поэтому структуру дискретной системы можно рассматривать в виде:

ДФ – дискретный фильтр

ФИ – формирователь импульсов управления

О – объект управления

Д – аналоговый датчик

к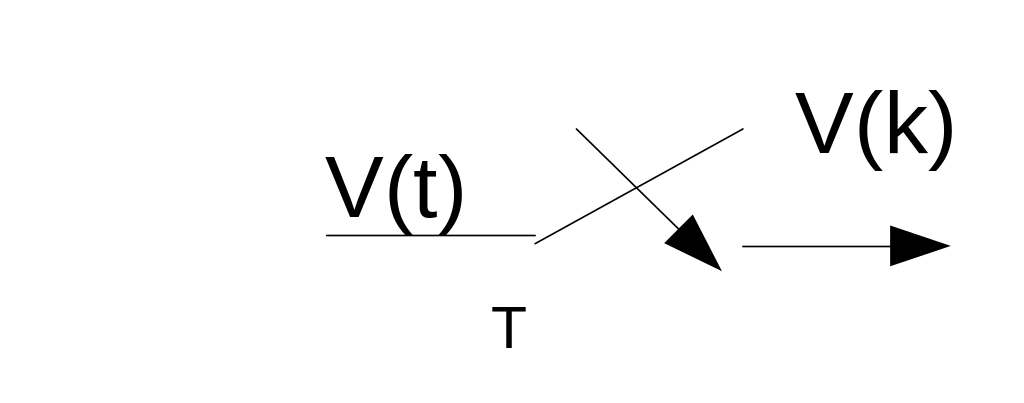 люч:

Т – период замыкания ключа на бесконечномалое

время

Решетчатая функция:

V(0) = V(t), t = 0

V(1) = V(t) и т.д.

V(k) =

V(t) V(kT) = V(k) = V_k

Аналогичным преобразованиям подвергается сигнал y(t) y(k)

Если дискретный фильтр является импульсным устройством, то он оперирует разностью: ε(k) = V(k) – y(k)

Если ДФ – цифровое устройство, то будем считать, что ε(k) ε*(k)

Разрядность кода достаточно велика, т.е. шаг квантования мал. Это позволяет одинаково анализировать как импульс, так и цифровой системы.

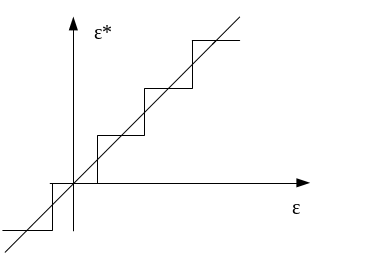
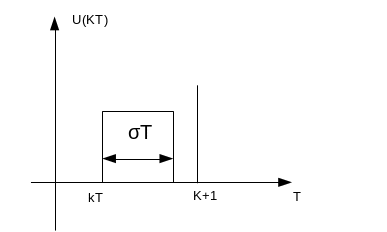
Для цифрового сигнала ФИ – это ЦАП.

U(kT) =

0

ЦАП можно рассматривать как ФИ при σ = 1

Д ля анализа подобных систем используются дискретные модели, которые позволяют определить зависимость между отдельными отсчетами.

y(t) kT

y(k,ε) = y ((k+ε)T) смещенная решетчатая функция:

62. Разностные уравнения

f(t) f(kT) = f(k) , k = 0, 1, 2

f́ (t) ~ Δ f(k) = f(k+1) – f(k) – классическая разность вперед

f(k) = f(k) – f(k-1) - классическая разность назад

f ″(t) ~ Δ² f(k) = Δ f(k+1) – Δ f(k) = f (k+2) – 2f(k+1) + f(k)

f ^m (t) ~Δ^m f (k) =

Дифференциальным уравнениям будут соответствовать разностные уравнения:

1. C₀ y(k+n) + C₁ y(k+n+1) +…+ C_n-1 y(k+1) + C_n + y_k = b₀ V(k+m) + b₁ V(k+m+1) +…+ b_m V(k)

2. C₀ y(k) + C₁ y(k - 1) + …+ C_n y(k - n) = b₀ V(k+m–n) +…+ b_m V(k - n)

Чтобы решить эти уравнения, необходимо задать начальные условия:

y(k+n-1), …, y(k) – вектор начальных условий

y(k - 1), …, y(k - n) – аналогично

Рассмотрим однородные разностные уравнения:

C₀ y(k) + C₁ y(k - 1) + …+ C_n y(k - n) =0

y(k) = С₁Z + С₂Z + …+ С_nZ

где Z_i – корни характеристического уравнения C₀Zⁿ + C₁Z^n-1 + …+ C_n = 0, i =

C _i – произвольная постоянная из вектора НУ, i =

Если определен вектор НУ, то разностные уравнения можно решить рекуррентно.

y(k)→0, k→∞,

Равномерная асимптотическая устойчивость:

63. Z – Преобразование.

Преобразование Лапласа позволяет алгебраизовать дифференциальные уравнения. Для дискретных систем аналогичную роль играет Z – преобразование, которое алгебраизовывает разностные уравнения. Z – преобразование получают путем модификации преобразования Лапласа для решетчатых функций.

F*

e^sT = Z

Z - Z – преобразование решетчатой функции

Z – преобразование обладает следующими свойствами:

1. преобразование линейно

f(t) =

2. изображение простейших функций

δ(k) – играет роль δ – функции для аналогичных сигналов

f(k) = δ(k) =

Z{ δ(k)} = 1*Z⁰ = 1

f(k) = 1(k) = 1, k = 0, 1, 2,…

3. Z{1(k)} = 1*Z⁰ + 1*Z^-1 + … =

f(k) = kT, k = 0, 1, 2,…

Z{kT} = T(0* Z⁰ + 1*Z^-1 + 2*Z^-2 + …) = TZ^-1(1 + 2 Z^-1 +3 Z^-2 + …) = TZ^-1 (1 + Z^-1 + Z^-2 + …) = =

f(k)

Z{f(k+1)} - ?

Z{f(k+1)} = f₁* Z⁰ + f₂* Z^-1 +… = Z⁺¹{ f₁* Z^-1 + f₂* Z^-2 + … + f₀ - f₀} = Z*F(Z) - f₀

F(Z) = f₁* Z^-1 + f₂* Z^-2 + … + f₀

f(0) = 0, Z – оператор сдвига на 1 период квантования

Z{f(k-1)}= Z^-1F(Z)

Передаточные функции дискретных систем.

64. Передаточная функция дискретного фильтра.

α₀ y(k+n) + α₁ y(k+n-1) +…+ α_n y(k) = β₀ ε(k+m) + β₁ ε (k+n-1) +…+ β_m ε(k) (1)

Преобразуем левую и правую части разностного уравнения (1) с помощью Z – преобразования:

(α₀*Zⁿ + α₁*Z^n-1 + … + α_n) y(Z) = (β₀*Z^m + β₁*Z^m-1 + …+ β_m) E(Z)

W_дф(Z) = - ПФ дискретного фильтра

C(Z) = , B(Z) =

ПФ дискретного фильтра является полным аналогом передаточной функции непрерывных систем:

C(Z) = 0, Z_i , i = - полюсы ПФ

B(Z) = 0, r_i, i = - нули ПФ

65. Передаточная функция формирователя импульсов и объекта.

U(kT) =

Для определения ПФ формирователя импульсов рассматривают следующую модель:

1. Пусть момент к = 0, U(k) = 0, k = 1, 2,…

U(0*T) = 1(t) – 1(t – σT)

L {U(0*T)} =

U(0*T) – ИПХ формирователя импульсов

W_фи(s) = L{ U(0*T)}

W_фи(s) =

ПФ формирователя импульсов рассматривают всегда вместе с объектом, т. к. они соединены последовательно, то W_фи(s)*W₀(s) =

Для нахождения дискретной модели этого соединения:

W₀(Z) = Z{L^-1{ W_фи(s) *W₀(s)}}

Необходимо найти решетчатую функцию, соответствующую этой ИПХ:

W₀(Z) =

W₀(s)*1/s – приведенная ПФ объекта

Приведенная ПФ совпадает с переходной характеристикой объекта. Таким образом, для определения ПФ требуется:

1. определить h(t) = L^-1{W₀(s)*1/s} – ПХ объекта управления

2. t = kT, k = 0, 1, 2,… h(k) – решетчатая функция

3. найти изображение W₀(Z) = Z{h(kT)}

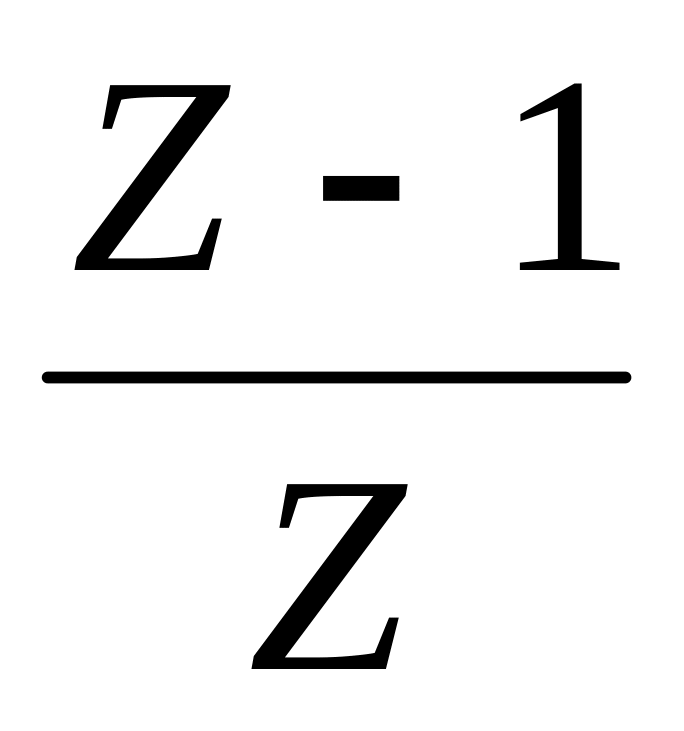
Пример определения ПФ W₀(Z): ОУ – апериодическое звено с коэффициентом усиления к₁ и постоянным временем Т₁

W₀(s) = , σ = 1

1. L^-1{W₀(s)*1/s} = k₁(1-e ^{–α t}), α₁ =

2. решетчатая функция h(k) = k₁(1-e ^{–α k T}), Т – период квантования

3. Найдем Z – изображение:

Z{h(k)} =

= k₁[(1+Z^-1+Z^-2+…)Z^-1 – e^{-α T}Z^-1(1+e^{-α T}Z^-1+e^{-2 α T}Z^-2+…)] = k₁

Z{h(k)} = k_{1 ,} d = e^{-α T}

W₀(Z) = - ПФ

Рассматривая ПФ, соответствующую дискретной модели, позволено рассматривать модель в 2-х видах:

Z^-1 – оператор запаздывания

Z – оператор опережения

ε(k) = ε(kT), k = 0, 1,…

y(Z) = E(Z)*W(Z)

Особенность этой системы – квантование сигнала рассогласования.

Найдем ПФ замкнутой системы:

E(Z) = V(Z) – y(Z)

y(Z) = W(Z)(V(Z) – y(Z))

W(Z) = W_дф*W₀(Z)

Ф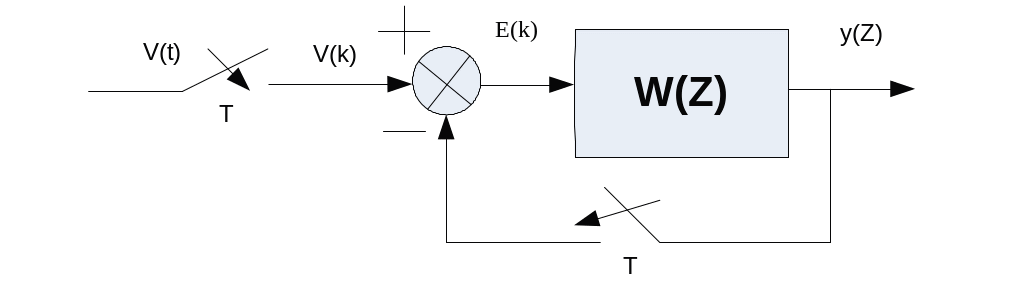 (Z) = y(Z)/V(Z) =

W(Z) – ПФ разомкнутой системы

Ф(Z) – ПФ замкнутой системы

(*) ε(t) = V(t) – y(t)

y(k) E(k)*W(Z)

(**) E(k) = V(k) – y(k-1)

Ф(Z) = y(Z)/V(Z) =

(*) и (**) – уравнения замыкания

Объект может описываться не только уравнениями входных – выходных(ПФ), но и уравнениями состояния.

66. Передаточная функция объекта, описанного уравнениями состояния при кусочно-постоянном уравнении.

x́(t) = Ax(t) + BU(t) – уравнение состояния объекта

y(t) = Cx(t) – уравнение выхода

U(t) = U(kT) = U_k, t [kT,(k+1)T]

Найдем дискретную модель объекта при y(k) = y(t) , t = kT

Рассмотрим общее решение уравнения:

x(t) = e^A x(t₀) + B U(τ)dτ

t₀ = kT, t = (k+1)T

x(k+1) = e^ATx(k) + B U(τ)dτ

Учтем, что

1. U(τ) =

(k+1)T-τ = σ

x(k+1) = e^AT x(k) +

A_d = e^AT, detA

B_d =

x(k+1) = A_d x(k) + B_d U(k)

y(kT) = C x(k)

e^AT = A_d

1. e^AT = L^-1{(sI-A)^-1}

2. t = T

3. e^AT

Zx(Z) = A_d x(Z) + B_d U(Z)

y(Z) = C x(Z)

x(Z) = (ZI - A_d)^-1 B_d U(Z)

y(Z) = C (ZI - A_d)^-1 B_d U(Z)

W(Z) = C (ZI - A_d)^-1 B_d

67. Устойчивость дискретных систем.

Устойчивость определяется корнями характеристического уравнения.

1 . Для модели вход – выход:

Ф(Z) =

W(Z) = - ПФ разомкнутой

системы

ПФ замкнутой системы:

Ф(Z) = , где Д(Z) = D(Z) + C(Z) – характеристический многочлен замкнутой системы

Д(Z) = 0, Z_i , i = ,

Д(Z) * y(k) = 0

y(k) = , где Z_i – корни характеристического уравнения

C_i – произвольная постоянная

Если y(t) 0 при к ∞, то тривиальное решение уравнения Д(Z) * y(k) = 0, y(k) = 0

называется равномерным асимптотически устойчивым. Необходимое и достаточное условие:

i = , x_св[n]→0, n→0

Для анализа устойчивости разрабатываются примерные устойчивости дискретных систем, которые аналогичны критической устойчивости непрерывной системы.

Если корни принадлежат площади этого круга, то система

устойчива; если за пределами круга, то неустойчива; если

на границе, то будут периодические колебания.

i = ,

y[k]→0, k→0, y[k]

y[k] =

, y(k)→0, k→∞

y(k) →∞, k→∞ - система неустойчива

W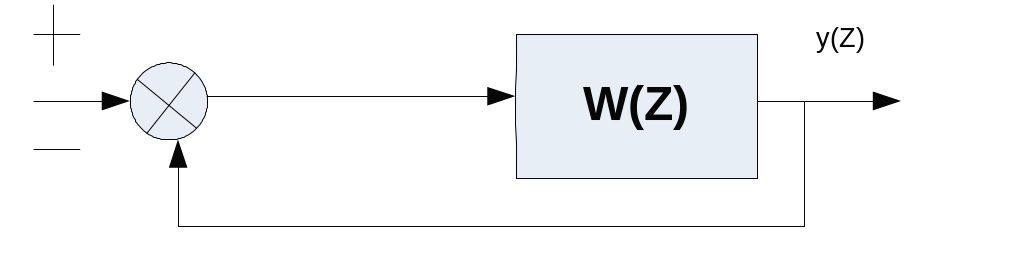 (Z) =

Характеристический многочлен замкну-

той системы:

Ф(Z) = = =

Если есть система автоматического управления (MATLAB, MathCad), то достаточно применить оператор для нахождения корней. Если выбрать W(Z, k₁, T₁),то Д(Z, k, T₁).

k₁ [k_1min, k_1max], T₁ [T_1min, T k_1max],

Z_i (k₁, T₁) – траектория корней характеристического уравнения i = ,

Часто для описания дискретной модели используются уравнения состояния:

x[n+1] = A_d x(k) + B_d U(k)

y(k) = C_d x(n)

x(k) Rⁿ

U(k) R^m

y(k) R^l

Исследование устойчивости такой системы связано с оценкой корней характеристического уравнения системы.

det (ZI - A_d) = 0

Раскрытие определителя при больших n сопровождается ошибкой округления (ошибки счета). Ошибки счета могут привести к тому, что корни будут существенно отличаться от истинных.

Z_i = Z_i (A_d) , i = ,

Поэтому при определении устойчивости стараются избежать:

Д(Z) = det (ZI - A_d) – характеристический многочлен

Для этого используют критерии устойчивости. Среди них выделяют критерий Зубова:

A_d2 = A

А_d4 = A * A и т.д.

Если A_d2n→0, то все корни лежат внутри единого круга, зн., система устойчива.

Если , то среди корней есть такие, которые не лежат внутри окружности, зн., и система неустойчива.

68. Анализ качества дискретных систем.

Методология анализа качества дискретных систем аналогична методологии анализа качества непрерывных систем. Анализ качества дискретных систем в 2-ч режимах:

- в установившемся режиме

- в переходных процессах

Анализ в установившихся режимах сводится к определению показателей качества переходной характеристики. Рассмотрим этот анализ более подробно:

69. Анализ ошибок воспроизведения входных сигналов.

W₁(Z) – цифровой регулятор

W₂(Z) - отраженная ПФ объекта управления

1. ошибка по входу: E(Z) = Ф_ε (Z) V(Z)

2. E_f(Z) = Ф_f(Z) F(Z)

Ф_ε (Z) = - ПФ по ошибке воспроизведения входного сигнала

Ф_f(Z) = - ПФ по возмущению

Е_п(Z0 = Z{e(k)} = E(Z) + E_f(Z) = Ф_ε (Z) V(Z) + Ф_f(Z) F(Z) – полная ошибка

Анализ этих ошибок производится по действию типовых сигналов.

V(k), f(k) – типовые сигналы, к = 0, 1, 2,…

В качестве типовых сигналов используют дискретные полиномиальные сигналы.

g(k) – типовой сигнал (дискретный полиномиальный сигнал порядка r)

g₀(k) = 1(k), к = 0, 1, 2,…

g₁(k) = kT, к = 0, 1, 2,…

g₂(k) = , к = 0, 1, 2,…

g_r(k) = , к = 0, 1, 2,…

При r = 0 1(t) 1(k)

При r = 1, t kT

При r = 2,

g₀(k) – статические ошибки

Е_ст(t) = Ф_ε (Z) * - изображение статической ошибки

Е_cк(Z) = Ф_ε (Z) * - изображение скоростной ошибки

Е_уcк(Z) = Ф_ε (Z) *

Величины этих ошибок оценивают исходя из теоремы о конечных значениях:

g(nT), n = 0, 1, 2,… - решетчатая функция

Z{g(n)} = G(Z)

lim g(kT) = lim (Z-1) G(Z)

_{k→∞ k→∞}

Значения ошибок зависят от порядка астатизма дискретной системы и от порядка дискретного полинома.

υ – порядок астатизма

r – порядок дискретного полинома

Включим сумматор в цепь прямой передачи сигнала.

y(k) =

Z{y(k)} = y(0)Z⁰ + y(1)Z^-1 + y(2)Z^-2 + …= g(0)Z⁰ + (g(0) + g(1))Z^-1 + (g(0) + g(1) + g(2))Z^-2 + …=

= g(0) (1 + Z^-1 + Z^-2 + …) + g(1) Z^-1 (1 + Z^-1 + …) + g(2)Z^-2 (1 + Z^-1 + …) = G(Z)

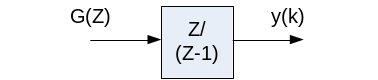
W_∑(Z) =

W(Z) =

W₀(1) = 1

Ф_ε (Z) =

ε_ст = lim (Z )

1. υ = 0 – статическая ошибка в статической системе

ε_ст =

V(n) = a₀ 1(t)

ε_ст = a₀ / (1+k)

2. υ = 1, 2,… ε_ст = 0

r = 1

ε_сk = lim (Z→1)

a) υ = 0 ε_сk = ∞

b) υ = 1 ε_сk = ε_сk =

V[n] = a₁nT, T>0

c) υ = 2, 3,… ε_сk = 0

r = 2 V(n) =

ε_усk = lim (Z→1)

υ = 0, 1 ε_усk = ∞

υ = 2 ε_усk =

Аналогичные ошибки возникают при действии полиномиального возмущения:

W₁(Z) =

W₂(Z) =

W(Z) =

70. Типовые законы регулирования, реализующиеся цифровыми регуляторами.

1. П – закон

2. И – закон

3. ПИ – закон

4. ПИД – закон

5. ПД – закон

П – закон:

U(k) = k_p - коэффициент усиления регулятора

U(Z) = k_p E(Z)

W_п(Z) = k_p =

И – закон:

U(k) = k_и

U(Z) = k_и

W_и(Z) = , υ = 1

ПИ – закон:

U(k) = k_р e(k) + k_и

U(Z) = (k_р + k_и

W_пи(Z) = , υ = 1

Быстродействие законов аналогично быстродействию непрерывных законов.

ПИД – закон:

U(k) = k_р e(k) + k_и + k_д(e(k) – e(k-1))

U(Z) = (k_р + + k_д(1-Z^-1))E(Z)

W_пид(Z) = k_р + + k_д

ПД – закон:

самостоятельно!

71. Анализ качества переходных процессов дискретных систем.

1. Рассмотрим дискретную модель системы:

Для анализа качества переходных процессов дискретных систем используют те же подходы, что и для непрерывных систем. Качество переходных процессов оценивается по переходной характеристике. Переходная характеристика – это реакция системы на единичный скачок при нулевых входах и нулевых начальных условиях.

1(k) = 1, k = 0, 1, 2,…

Данная структура имеет 2 входа, поэтому структура имеет 2 переходных характеристики:

1. V (k) = 1(k), f(k) = 0

Переходная характеристика по входу h(k)

2. f(k) = 1(k) , V(k) = 0

h_f(k), k = 0, 1, 2,… - переходная характеристика по возмущению

σ - ПИ – регулятор

h_m = max h (k)

_k

h_уст – установившееся значение переходной характеристики

h_уст = lim (Z-1) H(Z) при Z→1

H(Z) = Z{h(k)}

Значение σ не всегда будет точно отражать ПИ – регулятор. Если же нужна более точная оценка ПИ-регулятора, то вместо обычного Z – преобразователя надо использовать смещенную или модификацию Z – преобразования. Для построения переходной характеристики можно использовать следующие функции:

1. h(k), h_f(k)

H(Z) H_f(Z)

H(Z) = Ф(Z)

H_f(Z) =

2. Формулы обращения Z - преобразований

h(k) = Z^-1{H(Z)}

H_f(Z) = Z^-1{ H_f(Z)}

Существует несколько путей вычисления формул обращения Z- преобразований:

а) теорема разложений

Пусть H(Z) =

Теорема использует полюсы

Z_i = 1 Д(Z) = 0 Z₂,…,Z_n+1

h(k) =

Д́(Z_i) =

На основе разложения в ряд Лорана:

H(Z) = Ω₀ + Ω₁Z^-1 + Ω₂Z^-2 + …

H(Z) = h(0) + h(1) Z^-1 + h(2) Z^-2 + …

Ω₀ = h(0), Ω₁ = h(1), … ,Ω_k = h(k), k = 0, 1, 2,…

B(Z) = β₀Z^m + β₁Z^m-1 + … + β_m

Д(Z) = α₀Zⁿ + α₁Z^n-1 + … + α_n

Особенность дискретной системы: принципиальная возможность построения системы с конечной длительностью ПП.

Если Д(Z) = Zⁿ, Zi = 0, i = , то ПП будет длиться n шагов.

B(Z) = 1

72. Пример определения пх.

1. ДФ представляет собой П – закон регулирования К_д; W_д(Z) = К_д

2. Формирователь в виде ЦАПа (фиксатор нулевого порядка)

W_ф(Z) =

3. Объект W₀(s) =

W₀(Z) = Z{h₀(k)}

h₀(k) – h₀(t), t = kT; ПХ непрерывного объекта

Определим ПФ W₀(Z)

h₀(t) = k₁ - = k₁ (1 – e^-αT); α =

h₀(k) = k₁( 1(k) – d^-αkT)

Z{ h₀(k)} = k_{1 = ,} где d = e^-αT – период квантования

Определим ПФ разомкнутой системы:

W(Z) = W_д(Z) * W_ф(Z) * W₀(Z) = k_д

Найдем ПХ по входу:

H(Z) =

h(k) = Z^-1{H(Z)}

Если для описания динамики системы используют разностное уравнение системы, то их решение получают рекуррентным вычислением его ординат.

Литература:

1. Бесекeрский В. А., Попов Е. П. Теория систем автоматического управления.

. Изд. 4-е Санкт-Петербург. Изд. «Профессия» 2004 г.

2. Методы классической и современной теории автоматического управления в 5-ти томах под ред. Н. Д. Егупова, М. 2000г. Т. 1, т.2

3. Мирошник И. В. Теория систем автоматического управления. Линейные системы СПб. 2005

4. Теория автоматического управления под ред. А. А. Воронова. М.: 1986 г. Часть 1 (2)

5. Афанасьев, Калмановский, Носов Математическая теория конструирования систем управления, М.: 1989г.

6. Теория автоматического управления под редакцией Яковлева, М. 2003г.

7. Певзнeр Л. Д. Теория систем управления, М.: 2002 г.

8. Шишмарев В.Ю. Основы автоматического управления.- М.: «Академия», 2008 г.

104