разные поправки, что и было сделано в самых первых спектральных исследованиях, см. (3.1.3). С увеличением n поправки s, p, d в (3.1.3) уменьшаются, но незначительно, оставаясь одного порядка [1].
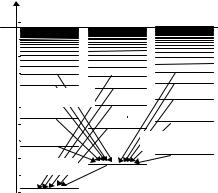
Рис. 3.3.4. Электронные орбитали атома Cs и схема электронных переходов в главной. 1-й и 2-й побочных сериях при излучении. Предел сходимости всех типов термов общий и соответствует энергии иона Cs+. Предел сходимости главной серии равен 3,89 эВ, потенциалу ионизации Cs, побочных – на 1,38 эВ меньше.
|
E |
|
d |
0 |
s |
p |
|
n |
|
|
|
11 |
|
|
|
10 |
2-я побочная |
|
|
9 |
|
|
|
8 |
|
|
|
7 |
|
|
1-я побочная |
|
|
|
|
|
главная |
|
|
6 |
|
|
|
Следующий существенный результат квантовой теории – правила отбора для оптических переходов. На изменение главного квантового числа ограничений нет, но орбитальное квантовое число должно измениться на ±1. Это объясняет закономерность чередования поправок в главной и побочных сериях, см. (3.1.3) и существо самих серий.
В основном состоянии щелочного атома его валентный электрон находится на орбитали ns. У атома Cs – 6s, см. рис. 3.3.4. Первый разрешенный оптический переход – на орбиталь 6р, остальные линии этой серии, названной главной, – на 7р, 8р… Тот же спектр может проявиться и в излучении, в переходах из высоких р-состояний на 6s (а так же на 7s… и т.д.). Но в излучении, при возбуждении, обеспечивающем заселение всех верхних состояний, переход может произойти и в 6р- состояние. 1-я побочная серия – переходы из d-состояний, 2-я побочная
– из s-состояний, см таблицу на стр. 202.
3.3.2.3.Ридберговские серии в молекулярных спектрах
Радиусы ридберговских орбиталей быстро растут с увеличением главного квантового числа, пропорционально n2, см. (3.2.9). Уже при n = 10 он превышает 5 нм, но при этом система остается довольно устойчива. Энергия связи составляет ≈ 0,14 эВ. Состояние электрона на такой орбитали мало зависит от того, находится в центре ее атомный или молекулярный ион, если его размер много меньше этих 5 нм. Ведь
209
выражение (3.2.9) получено как решение задачи о состоянии электрона в центральном поле. На больших расстояниях поле любого иона можно рассматривать как центральное.
Таким образом, у любой молекулы имеется спектр ридберговских возбужденных состояний, и, соответственно, спектры оптических пе-
реходов электронов из невозбужденных, основных состояний, в эти
ридберговские состояния. Причем – любых электронов, не обязательно валентных. Подобные серии наблюдались и в спектрах возбуждений остовных электронов. Естественно, правила отбора сохраняются и типы ридберговских состояний, в которые возможен оптический переход, зависят от типа исходного состояния.
Так же, как и в атомах, ридберговские термы сходятся к ионизационному пределу, к нулевой энергии связи электрона с оставляемым ионом, а оптический предел сходимости равен потенциалу ионизации возбуждаемых электронов. Первые точные измерения потенциалов ионизации сложных молекул сделаны именно оптически, анализом ридберговских серий в их спектрах поглощения.
210