9

Лабораторная работа № 17-1. Б-207.

ИССЛЕДОВАНИЕ 3АТУXAЮЩИХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ.

Основные понятия.

Если в проводнике изменяется сила тока, то в нем возникает электродвижущая сила самоиндукции (ЭДС), препятствующая этому изменению Е = - L . (1)

Коэффициент пропорциональности L называется коэффициентом самоиндукции (индуктивностью). Величина его зависит от формы, размеров проводника и от магнитной проницаемости окружающей среды. Большой индуктивностью обладают катушки индуктивности, состоящие из многих витков. Если включить такую катушку в цепь переменного тока, то в ней возникает ЭДС самоиндукции, препятст­вующая изменению тока (1). Это приводит и появлению индуктивного (реактивного) сопротивления катушки X_l , которое может пре­восходить ее активное сопротивление R. Включение в цепь переменного тока конденсатора С приводит к возникновению емкостного сопротивления X_С. Рассмотрим теперь цепь, состоящую из последовательно соеди­ненных: сопротивления R, индуктивности L, и емкости С. Такая цепь называется колебательным контуром (рис. 1). Как известно, если зарядить конденсатор С, а затем отключить источник питания, то в колебательном контуре возникнут электрические колебания.

В процессе колебаний энергия электри­ческого поля заряженного кoндeнcaтopa преобразуется в энергию· магнитного поля катушки индуктивности и, наоборот, энергия магнитного поля преобразуется в электрическую энергию. При протекании тока в контуре в активном сопротивлении выделяется джоулево тепло, что приводит к потере энергии и затуханию колебаний. В связи с этим с течением времени амплитуда колебаний уменьшается. / рис.2/.

Выведем уравнение этих колебаний. Запишем для контура 2-е правило Кирхгофа:

U + U_l = E , (2)

где U = IR – падение напряжения на сопротивлении R;

U_C = - разность потенциалов на обкладках конденсатора С;

E = - L - ЭДС самоиндукции катушки L.

Подставляя значения U, E в (2), получим

UR + U_C = - L . (3)

Поскольку q = U_C C , а I = = C и = C

Тогда, подставляя в (3) значение I, , получим

CR + U_C = -LC ,

Путем несложных преобразований (4) окончательно получаем

+ + = 0 . (5)

Выражение (5) и представляет собой дифференциальное уравнение колебаний, возникающих в колебательном контуре (рис. 1).

Решением этого уравнения является функция:

U_C = U₀ cos t ;

здесь

= - круговая частота; (6)

U_m = U₀ - амплитуда колебаний. (7)

Анализ решения уравнения (5) показывает, что колебательный процесс в контуре затухает, т.е. амплитуда колебаний уменьшается по экспоненциальному закону (7). Такие колебания называются затухающими, а величина называется коэффициентом затухания. Затухание колебаний обусловлено наличием в контуре активного сопротивления R (а также активной составляющей сопротивления катушки индуктивности L). В идеальном случае, когда R = 0, выражение (6) преобразуется к виду

=

и получается известная формула Томсона для периода колебаний колебательного контура

T = 2n (поскольку T = ).

Характер изменения амплитуды колебаний

U_m = U₀

может быть представлен графически (рис. 2).

Отношение двух последовательных амплитуд U_mk и U_m(k+1) (7), отстоящих друг от друга во времени на период колебания Т:

= =

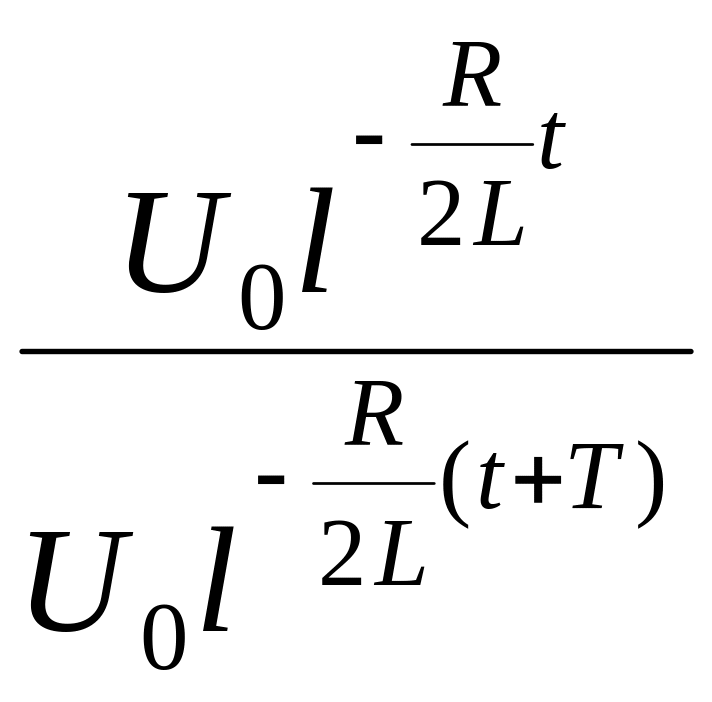и называется декрементом затухания.

Соответственно логарифм этого отношения

ln =

называется логарифмическим декрементом затухания.

Лабораторная работа исследование затухающих колебаний в колебательном контуре

Цель работы: Изучение затухающих колебаний.

Приборы и принадлежности: Осциллограф, колебательный контур, звуковой генератор ГЗ – 111.

Методика и техника эксперимента

К олебательным контуром называется цепь, состоящая из конденсатора С, катушки индуктивности L и омического сопротивления R. Если зарядить конденсатор до разности потенциалов U, а затем дать ему возможность разряжаться через индуктивность L, то в колебательном контуре возникают свободные колебания тока, заряда на обкладках конденсатора и напряжения между обкладками конденсатора. В процессе колебаний, энергия электрического поля заряженного конденсатора преобразуется в энергию магнитного поля катушки индуктивности и, наоборот, энергия магнитного поля преобразуется в электрическую энергию. При протекании тока в контуре в активном сопротивлении выделяется джоулево тепло, что приводит к потере энергии и затуханию колебаний. В связи с этим, с течением времени амплитуда колебаний уменьшается так, как показано на рисунке.

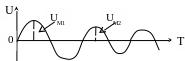
Выведем уравнение затухающих колебаний. Полагая, что мгновенные значения токов и напряжений удовлетворяют законам, установленным для цепей постоянного тока, применим к колебательному контуру второе правило Кирхгофа:

I·R + U_С = ε_S, (6.1)

где IR – падение напряжения на резисторе; U_С = – напряжение на конденсаторе; ε_S = – L – ЭДС самоиндукции.

Так как I = , а q = C·U, тогда I = C . Найдем производную силы тока: . Подставляя эти выражения в уравнение (6.1), получим:

+ + = 0. (6.2)

Разделив уравнение (6.2) на LC получим:

+ + = 0. (6.3)

Выражение (6.3) представляет собой дифференциальное уравнение затухающих колебаний, возникающих в колебательном контуре.

Решением этого уравнения является функция:

U = U₀ cos(ωt+φ), (6.4)

где β = R/2L – коэффициент затухания.

Так как циклическая частота собственных колебаний контура равна

ω₀² = 1/LC, то уравнение (6.3) можно представить в виде:

+ 2β + ω₀²U = 0. (6.5)

U₀ = U_m – амплитуда затухающих колебаний;

ω = – частота затухающих колебаний; φ – начальная фаза.

Из выражения для частоты ω следует, что затухающие колебания в контуре возникают лишь в том случае, если: ω₀² >β²; > ; R < 2 .

Если R > , то колебания в контуре не возникают, а происходит, так называемый апериодический разряд конденсатора.

Для характеристики степени затухания колебаний, кроме коэффициента затухания β, используют также логарифмический декремент затухания.

Логарифмическим декрементом затухания λ называется натуральный логарифм отношения двух амплитуд напряжения U_m, разделенных интервалом времени, равным периоду колебаний Т:

λ = ln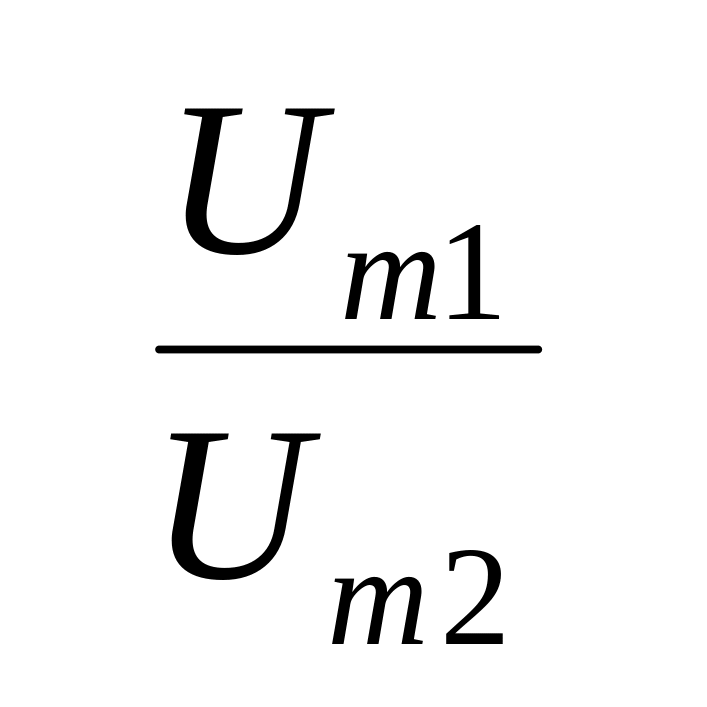 , (6.6),

где U_m1 = U₀ ; U_m2 = U₀ .

Подставив значения U_m в формулу (6.4), получим:

λ = β·T. (6.7)

Принципиальная схема для получения затухающих колебаний представлена ниже:

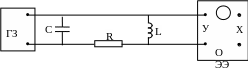
Она представляет собой колебательный контур, состоящий из конденсатора С, катушки индуктивности L и сопротивления R. Колебания в контуре наблюдаются с помощью осциллографа ОЭ. Для возбуждения колебаний служит звуковой генератор ГЗ-111.