Архив С / 3 семестр / Информатика / Экономика_1курс / Табличный процессор4

Решение финансово-экономических задач

1.Простые проценты

Основные понятия:

Процент – абсолютная величина дохода от предоставления денег в долг в любой его форме.

Процентная ставка – относительная величина дохода за фиксированный интервал времени, измеряемая в процентах или в виде дроби.

Период начисления – интервал времени, к которому приурочена процентная ставка.

Капитализация процентов – присоединение начисленных процентов к основной сумме.

Формула называется формулой простых процентов, где S – наращенная сумма в конце срока, P - первоначальная сумма долга, i – ставка простого процента (в годовом исчислении), n=T/t – количество периодов начисления процентов (T – срок ссуды, t – период начисления).

Проценты за весь срок рассчитываются по формуле: .

Задание1. Вы берете в банке ссуду в размере 100 млн. рублей на два года. Ставка составляет 30% годовых. Определить проценты за весь срок ссуды и сумму, образовавшуюся к концу срока ссуды.

!!! Практика расчета по простым процентам используется при выдаче кратковременных ссуд и на период не больше года, так что n может быть и меньшим 1. В этом случае , где z – количество дней, на которые взята ссуда, y - количество дней в году.

Величина z. При точном определении количества дней подсчитывается число дней между датой выдачи ссуды и датой ее возврата, причем день выдачи и день возврата считаются одним днем. При приближенном определении количества дней ссуды подсчитывается число полных месяцев между датой выдачи ссуды и датой ее возврата и количество дней сверх полного месяца. Количество дней в каждом месяце принимается равным 30.

Величина y. Точное количество дней соответствует 365 или 366. Чаще всего в банковских операциях используется приближенное количество дней, равное 360. Процент, подсчитанный с таким числом дней, называется коммерческим, или обыкновенным.

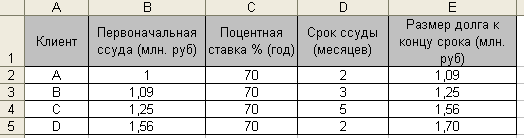
Задание2. Банк выдал ссуду на сумму 1 млн. рублей клиенту А на срок 2 месяца, затем деньги, полученные от клиента А, выдал клиенту В на срок 3 месяца. Деньги, полученные от клиента В, выдал клиенту С на 5 месяцев, наконец, деньги, полученные от клиента С, - клиенту D на 2 месяца. Все ссуды были даны под 70% годовых. Какую сумму вернет банку клиент D? Произвести расчет методом простого коммерческого процента.

2.Сложные проценты

Основные понятия:

Капитализация процентов – присоединение начисленных процентов к основной сумме.

Сложный процент – метод начисления, при котором проценты, полученные за год, прибавляются к первоначальной сумме вклада (долга банка перед клиентом), т.е. капитализируются, и в последующем году проценты начисляются уже на эту новую сумму.

Формула , где P - первоначальная сумма долга, i – процентная ставка (например, если процентная ставка 70, то i=70/100), n – количество периодов начисления.

Задание3. Банк выдал ссуду на сумму 1 млн. рублей клиенту А на срок 2 месяца, затем деньги, полученные от клиента А, выдал клиенту В на срок 3 месяца. Деньги, полученные от клиента В, выдал клиенту С на 5 месяцев, наконец, деньги, полученные от клиента С, - клиенту D на 2 месяца. Все ссуды были даны под 70% годовых. Какую сумму вернет банку клиент D? Произвести расчет методом сложных процентов.

3.Финасовые функции

Финансовые функции присутствуют в Пакете Анализа. Для их использования необходимо выбрать Сервис→Надстройки→Пакет Анализа.

БЗ – будущая стоимость, рассчитывает будущую стоимость инвестиций на основе периодических постоянных платежей и постоянной процентной ставки. ЛТ;ПС;ТИП). Изучите синтаксис функции, используя справку.

Все аргументы, означающие деньги

Синтаксис: БС (СТАВКА;КПЕР;П, которые вы платите, представляются отрицательными числами, а деньги, которые вы получаете, представляются положительными числами.

Задание4. Гражданин желает поместить 100 000 руб. на 5 лет под сложную ставку в 15% годовых. Определить размер вклада по окончании срока, используя два способа решения задачи: по формуле сложных процентов и с использованием встроенной функции.

Задание5. Какую сумму необходимо положить в банк, чтобы через 5 лет получить 201 136 руб. при использовании схемы сложного процента с ежегодным начислением процентов и годовой ставкой 15%? Решить задачу, используя два способа решения задачи: по формуле сложных процентов и с использованием встроенной функции.

ПС – функция, обратная к функции БС и позволяющая определить первоначальный объем вклада. Изучите синтаксис функции, используя справку.

Если выплаты осуществляются ежемесячно, то процентная ставка за месяц составит процент/12, ежеквартально, то процент/4.

Если ссуда дана на 4 года с ежемесячными выплатами, то периодов выплат будет 4·12=48.

Решите следующие задачи, используя встроенные финансовые функции (все решения на одном листе книги).

1.Определите, какая сумма окажется на счете, если вклад размером 900 руб. положен под 9% годовых на 19 лет, а проценты начисляются ежеквартально.

Ответ: 4883 руб.

2.Какая сумма должна быть выплачена, если 6 лет назад была дана ссуда 1500 руб. под 15% годовых с ежемесячным начислением процентов?

Ответ: 3669 руб.

3.Определите необходимую сумму текущего вклада, чтобы через 12 лет он достиг 5000 руб., если процентная ставка по нему составляет 12%.

Ответ: 1283 руб.

4.Взносы на сберегательный счет составляют 200 руб. в начале каждого года. Определите, сколько будет на счете через 7 лет при ставке 10%.

Ответ: 2087 руб.

5.Есть два варианта вложения средств в сумме 300 тыс. руб. в течении 4 лет: в начале каждого года под 26% и в конце каждого года под 38% годовых. Определите, сколько денег окажется на счете для каждого варианта через 4 года.

Ответ: 756142 руб.; 1088022 руб.

!!! Для выполнения задания изучите функцию КПЕР, назначение всех ее аргументов.

6.Ссуда в 5000 руб. погашается ежемесячными платежами по 141,7 руб. Через сколько лет произойдет погашение ссуды, если годовая ставка процента 16% (используется функция КПЕР).

Ответ: 48 месяцев.

7.Рассматривается два варианта покупки дома: заплатить сразу 100000 руб. или платить в рассрочку в течении 15 лет по 9400 руб. ежемесячно. Какой вариант выгодней, если ставка процента 8% годовых?