
Возрастание и убывание функции
Возрастание
и убывание дифференцируемой функции
связано со знаком её производной.
Напомним, что функция ![]() называется возрастающей на
интервале
называется возрастающей на
интервале ![]() ,
если для любых двух точек
,
если для любых двух точек ![]() из
неравенства
из
неравенства ![]() следует,
что
следует,
что ![]() ; убывающей на
интервале
,
если из неравенства
следует,
что
; убывающей на
интервале
,
если из неравенства
следует,
что ![]() ; невозрастающей на
интервале
,
если из неравенства
следует,
что
; невозрастающей на
интервале
,
если из неравенства
следует,
что ![]() ,
и неубывающей на
интервале
,
если из неравенства
следует,
что
,
и неубывающей на
интервале
,
если из неравенства
следует,
что ![]() .
.
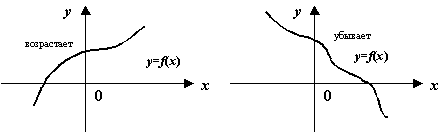
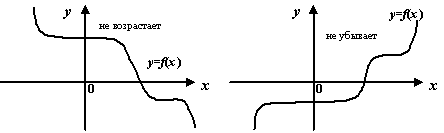
Рис.7.15.Графики возрастающей, убывающей, невозрастающей и неубывающей функций
Очевидно,
что функция
возрастает
тогда и только тогда, когда убывает
функция ![]() ;
аналогичное утверждение связывает
неубывающую функцию с невозрастающей.
;
аналогичное утверждение связывает
неубывающую функцию с невозрастающей.
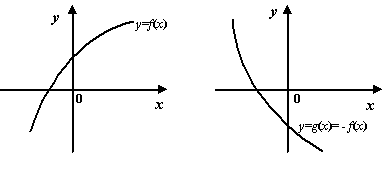
Рис.7.16.Графики функций и
Теорема 7.2 Пусть
функция
дифференцируема
на интервале ![]() и
и ![]() при
всех
при
всех ![]() .
Тогда
возрастает
на
.
Если же
.
Тогда
возрастает
на
.
Если же ![]() при
всех
,
то
не
убывает на
.
при
всех
,
то
не
убывает на
.
Аналогично,
если ![]() при
всех
,
то
убывает
на
,
а если
при
всех
,
то
убывает
на
,
а если ![]() при
всех
,
то
не
возрастает на
.
при
всех
,
то
не
возрастает на
.
Доказательство.
В силу предыдущего замечания, теорему
достаточно доказывать только для
случаев
и
.
Пусть
при
всех
и
,
.
Применим к отрезку ![]() формулу
конечных приращений:
формулу
конечных приращений:
![]()
где ![]() .
В правой части
.
В правой части ![]() и
и ![]() ,
так что
,
так что ![]() ,
откуда
,
что означает возрастание функции.
,
откуда
,
что означает возрастание функции.
Точно
так же, если
,
то получаем ![]() ,
откуда
,
что означает неубывание функции.
,
откуда
,
что означает неубывание функции.
Максимум и минимум функции.
Приведем
точные определения точек
экстремума.
Определение. Точка
x0 называется
точкой минимума функции f, если для всех
x из некоторой окрестности x0 выполняется
неравенство f(x) ≥ f(x0.
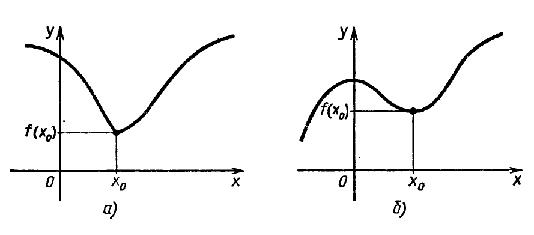
Это
наглядно показано на рисунке 1:
 рисунок
1
Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0.
Это
наглядно показано на рисунке 2:
рисунок
1
Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0.
Это
наглядно показано на рисунке 2:
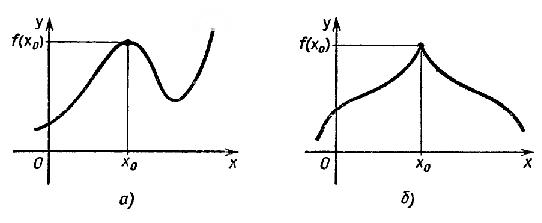 рисунок
2
По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно).
В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно).
Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже:
рисунок
2
По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно).
В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно).
Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже:
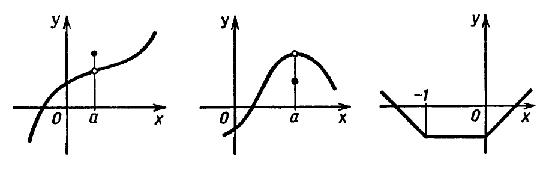 Слева
направо: a - точка максимума; a - точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума.
Для
точек минимума и максимума функции есть
общее определение - точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название - экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума - xmin.
Слева
направо: a - точка максимума; a - точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума.
Для
точек минимума и максимума функции есть
общее определение - точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название - экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума - xmin.
Список литературы.
Лит.: И л ь и н В. А., П о з н я к Э. Г., Основы математического анализа, 3 изд., ч. 1,М., 1971; КудрявцевЛ. <Д., Курс математического анализа, т. 1,2, М., 1981; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 1, М., 1975; [4] Б а х в а л о в Н. С., Численные методы, 2 изд., т. 1, М., 1975. Л. Д. Кудрявцев.
