Физический смысл производной

Ключевые слова: физический смысл производной, среднее ускорение материальной точки, сила и импульс, количество заряда, напряженность и потенциал

Понятие производной широко используется в современной физике. Приведем несколько примеров.

• Среднее ускорение материальной точки выражается формулой a= tv(t+ t)−v(t)

Мгновенное ускорение точки равно a=lim t 0 tv(t+ t)−v(t)=dtdv=v  

• Сила и импульс по второму закону Ньютона связаны соотношением F=dtdp=p .

• Количество заряда, прошедшего через поперечное сечение проводника, определяет силу тока: I=dtdq=q .

• В электростатическом поле, изменяющемся только по оси OX, напряженность и потенциал связаны соотношениемE=−dxd =− .

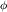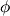Физический смысл производной x`(t) от непрерывной функции x(t) в точке t₀– есть мгновенная скорость изменения величины функции, при условии, что изменение аргумента Δt стремится к нулю.

Если  функция y = f(x) и ее аргумент x являются физическими величинами,  то производная   – скорость изменения переменной y относительно переменной x в точке .  Например, если S = S(t) – расстояние, проходимое точкой за время t,  то ее производная  – скорость в момент времени .  Если  q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени  t,  то   – скорость изменения количества электричества в момент времени , т.е. сила тока в момент времени .

Задачи.

Пусть точка движется по координатной прямой и закон ее движения (координата точки в момент времени  t) задается функцией   .   В момент времени     она находится в точке с координатой   ,  а в момент времени    – в точке с координатой   .  Тогда перемещение точки за промежуток времени     равно   . 

Величина     называется  средней скоростью  перемещения точки за промежуток времени   :

.

Предел средней скорости при     называется  мгновенной скоростью  точки в момент времени   :

.

При прямолинейном движении, совершаемом по закону   ,  мгновенная скорость точки в момент времени    равна значению производной функции     в точке     :

.

Аналогично определяется мгновенная скорость изменения других физических величин. Так, например, мгновенное ускорение (скорость изменения скорости) точки в момент времени    равно значению производной функции     в точке   :

                                   или

Пример 1.  Материальная точка движется прямолинейно по закону      .  Найдите мгновенную скорость точки в момент времени   .

Решение.

Ответ:  8 м/c

Пример 2.  Материальная точка массой  кг движется прямолинейно по закону     .  Найдите кинетическую энергию точки в момент времени   и равнодействующую всех сил, действующих на точку в этот момент.

Решение. Кинетическая энергия   вычисляется по формуле  , а равнодействующая F всех сил, действующих на точку, по формуле .

а)  откуда   и, следовательно,  ;

б)  откуда     и

Ответ:  1 Дж;   Н.

Московский приборостроительный техникум

Государственного образовательного учреждения высокого профессионального образования

Российский государственный торгово-экономический университет.

Самостоятельная работа по математике

На тему: «Геометрический смысл производной»

Студент: Валиев М.А.

Группа: Эк-119

Специальность: Компьютерные сети (230111)

Преподаватель: Балюк А.П.