
- •Основні властивості (аксіоми) належності точок і прямих на площині
- •Висота, бісектриса, медіана трикутника
- •Дотична до кола
- •Геометричне місце точок
- •Пряма й обернена теореми
- •Доведеннявід супротивного
- •Приклади розв’язування типових задач з геометрії для 7 класу
- •Теорема Піфагора
- •Симетрія відносно прямої
- •Множення вектора на число
- •Скалярний добуток векторів
- •Подібність прямокутних трикутників
- •Пропорційність відрізків хорд і січних кола
- •Вписані й описані чотирикутники
- •Теорема синусів
- •Розв’язування трикутників
- •Многокутники
- •Правильні многокутники
- •Паралельність прямих і площини
- •Ознака паралельності площин
- •Перпендикулярність прямих і площин
- •Перпендикуляр і похила
- •Відстань між мимобіжними прямими
- •Кут між мимобіжними прямими
- •Декартові координати та вектори в просторі
- •Перетворення в просторі
- •Подібність просторових фігур
- •Вектори в просторі
- •Тригранний і многогранний кути
- •Паралелепіпед
- •Правильні многогранники
- •Описані кулі
Подібність просторових фігур
Перетворення
фігури F
називається перетворенням
подібності,
якщо при цьому перетворенні відстані
між точками змінюють себе в одну й ту
саму кількість разів.
Як і на площині,
перетворення подібності в просторі
переводить прямі у прямі, півпрямі у
півпрямі, відрізки у відрізки і зберігає
кути між півпрямими. Перетворення
подібності переводить площини у
площини.
Аналогічно гомотетії на
площині визначається гомотетія
в просторі.
Гомотетія
є перетворенням подібності.
Перетворення
гомотетії у просторі переводить
довільну площину, яка не проходить через
центр гомотетії, у паралельну площину
(або в себе, якщо
).
На
рисунку:
;![]() ;
;
![]() ;
;![]() .
.

Вектори в просторі
Усі
основні означення векторів у просторі
залишаються такими самими, як означення
векторів на площині (див. розділ
«Геометрія. 8 клас»).
Координатами
вектора
,
де
![]() ,
,
![]() ,
називають числа
,
називають числа![]() ,
,
![]() ,
,
![]() .
Вектори
рівні тоді, й тільки тоді, коли вони
мають відповідно рівні координати. Це
дає підставу позначити вектор його
координатами
.
Вектори
рівні тоді, й тільки тоді, коли вони
мають відповідно рівні координати. Це
дає підставу позначити вектор його
координатами
![]() ,
або просто
,
або просто
![]() .
.
![]() .
Дії
над векторами в просторі позначають
так само, як і на площині:
.
Дії
над векторами в просторі позначають
так само, як і на площині:
![]()
![]() .
Діють
і геометричні правила: правило трикутника,
правило паралелограма, правило
многокутника.
Так само доводиться,
що
.
Діють
і геометричні правила: правило трикутника,
правило паралелограма, правило
многокутника.
Так само доводиться,
що
![]() ,
а напрям вектора
,
а напрям вектора
![]() збігається
з напрямом
,
якщо
,
і протилежний напряму
,
якщо
.
Зберігається
поняття колінеарних векторів і його
необхідна й достатня умова.
Скалярним
добутком векторів
збігається
з напрямом
,
якщо
,
і протилежний напряму
,
якщо
.
Зберігається
поняття колінеарних векторів і його
необхідна й достатня умова.
Скалярним
добутком векторів![]() і
і
![]() називається
число
називається
число
![]() .
Має
місце теорема, за якою скалярний добуток
векторів дорівнює добутку їх абсолютних
величин і косинуса кута між векторами:
.
Має
місце теорема, за якою скалярний добуток
векторів дорівнює добутку їх абсолютних
величин і косинуса кута між векторами:
![]() .
Для
того щоб два вектори були перпендикулярними,
необхідно й достатньо, щоб їх скалярний
добуток дорівнював нулю.
Кожний
вектор у просторі можна єдиним способом
розкласти за трьома координатними
векторами
.
Для
того щоб два вектори були перпендикулярними,
необхідно й достатньо, щоб їх скалярний
добуток дорівнював нулю.
Кожний
вектор у просторі можна єдиним способом
розкласти за трьома координатними
векторами
![]() ,
,
![]() і
і
![]() (див.
рисунок).
(див.
рисунок).

Геометрія. 11 клас
Многогранники
Двогранним
кутом
називається фігура, утворена двома
півплощинами зі спільною прямою, що їх
обмежує, —
ребром
двогранного кута. Півплощини називаються
гранями
двогранного кута.
Площина, перпендикулярна
до ребра двогранного кута, перетинає
його грані по двох півпрямих. Кут,
утворений такими півпрямими, називається
лінійним
кутом
двогранного кута (див. рисунок). За міру
двогранного кута приймається міра його
лінійного кута.
 Міра
двогранного кута не залежить від вибору
лінійного кута.
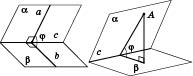
Побудувати лінійний
кут двогранного кута можна двома
способами.
1. Обрати точку на ребрі
кута й провести через цю точку
перпендикуляри до ребра, що лежать у
гранях кута (див. рисунок нижче зліва).
Кут між цими перпендикулярами — лінійний
кут даного двогранного кута.
2.
Обрати точку на грані двогранного кута
й опустити з неї перпендикуляри на ребро
кута та на іншу грань двогранного кута
(див. рисунок нижче справа). З’єднати
основи цих перпендикулярів. Кут між цим
відрізком і перпендикуляром, проведеним
до ребра двогранного кута, буде лінійним
кутом даного двогранного кута.
Міра
двогранного кута не залежить від вибору
лінійного кута.
Побудувати лінійний
кут двогранного кута можна двома
способами.
1. Обрати точку на ребрі
кута й провести через цю точку
перпендикуляри до ребра, що лежать у
гранях кута (див. рисунок нижче зліва).
Кут між цими перпендикулярами — лінійний
кут даного двогранного кута.
2.
Обрати точку на грані двогранного кута
й опустити з неї перпендикуляри на ребро
кута та на іншу грань двогранного кута
(див. рисунок нижче справа). З’єднати
основи цих перпендикулярів. Кут між цим
відрізком і перпендикуляром, проведеним
до ребра двогранного кута, буде лінійним
кутом даного двогранного кута.
Тригранний і многогранний кути
Нехай
промені a,
b,
c
виходять з однієї точки й не лежать в
одній площині.
Тригранним
кутом![]() називається фігура, яка складається з
трьох плоских кутів
називається фігура, яка складається з
трьох плоских кутів
![]() ,
,
![]() ,
,
![]() (див.
рисунок). Ці кути називаються гранями
тригранного кута, а їх сторони — ребрами.
Спільна вершина плоских кутів називається
вершиною
тригранного кута. Двогранні кути,
утворені гранями тригранного кута,
називаються двогранними
кутами тригранного кута.
Аналогічно дають означення многогранного
кута.
(див.
рисунок). Ці кути називаються гранями
тригранного кута, а їх сторони — ребрами.
Спільна вершина плоских кутів називається
вершиною
тригранного кута. Двогранні кути,
утворені гранями тригранного кута,
називаються двогранними
кутами тригранного кута.
Аналогічно дають означення многогранного
кута.
 Теорема
1. У тригранному куті кожний плоский кут
менший за суму двох інших.
Теорема
2. Сума плоских кутів тригранного кута
менша за
.
Теорема
1. У тригранному куті кожний плоский кут
менший за суму двох інших.
Теорема
2. Сума плоских кутів тригранного кута
менша за
.
Многогранники
Многогранник
—
це таке тіло, поверхня якого складається
із скінченної кількості плоских
многокутників. Многогранник називається
опуклим,
якщо він лежить по один бік від площини
кожного з плоских многокутників на його
поверхні. Спільна частина такої площини
й поверхні опуклого многокутника
називається гранню.
На
рисунку нижче зліва зображений неопуклий
многогранник; на рисунку справа —
опуклий.
 Грані
опуклого многогранника є плоскими
опуклими многокутниками. Сторони
граней називаються ребрами
многогранника,
а вершини граней — вершинами
многогранника.
Грані
опуклого многогранника є плоскими
опуклими многокутниками. Сторони
граней називаються ребрами
многогранника,
а вершини граней — вершинами
многогранника.
Призма
Призмою
називається
многогранник, який складається з двох
плоских многокутників, що лежать у
різних площинах і суміщаються паралельним
перенесенням, та всіх відрізків, що
сполучають відповідні точки цих
многокутників (див. рисунок). Многокутники
називаються основами
призми,
а відрізки, які сполучають відповідні
вершини, — бічними
ребрами призми.
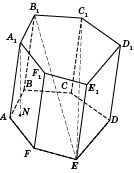 Позначення:
Позначення:
![]() .
Бічна
поверхня призми складається з
паралелограмів. Кожний із них має дві
сторони, які є відповідними сторонами
основи, а дві інші — суміжними бічними
ребрами. Основи призми рівні й лежать
у паралельних площинах. Бічні ребра
призми паралельні та рівні. Висотою
призми
називається відстань між площинами її
основ.
Відрізок, який сполучає дві
вершини призми, що не належать одній
грані, називається діагоналлю
призми.
(На рисунку
.
Бічна
поверхня призми складається з
паралелограмів. Кожний із них має дві
сторони, які є відповідними сторонами
основи, а дві інші — суміжними бічними
ребрами. Основи призми рівні й лежать
у паралельних площинах. Бічні ребра
призми паралельні та рівні. Висотою
призми
називається відстань між площинами її
основ.
Відрізок, який сполучає дві
вершини призми, що не належать одній
грані, називається діагоналлю
призми.
(На рисунку
![]() —
висота,
—
висота,
![]() і
і
![]() —
діагоналі.)
Діагональні
перерізи
— це перерізи призми площинами, що
проходять через два бічних ребра, які
не належать одній грані (див.
рисунки).
—
діагоналі.)
Діагональні
перерізи
— це перерізи призми площинами, що
проходять через два бічних ребра, які
не належать одній грані (див.
рисунки).
 Призма
називається прямою,
якщо її бічні ребра перпендикулярні до
основ. У протилежному випадку призма
називається похилою.
Бічні
грані прямої призми — прямокутники,
висота прямої призми дорівнює бічному
ребру, діагональні перерізи є
прямокутниками.
Бічною
поверхнею призми
називається сума площ бічних граней.
Повна
поверхня призми
дорівнює сумі бічної поверхні й площ
основ.
Теорема 1. Бічна поверхня прямої
призми дорівнює добутку периметра
основи та висоти, тобто довжини бічного
ребра.
Перпендикулярним
перерізом призми
будемо називати переріз площиною,
перпендикулярною до бічного ребра
призми (а це означає, що ця площина є
перпендикулярною до всіх бічних ребер
призми).
Теорема 2. Бічна поверхня
похилої призми дорівнює добутку довжини
бічного ребра і периметра перпендикулярного
перерізу.
На рисунку
Призма
називається прямою,
якщо її бічні ребра перпендикулярні до
основ. У протилежному випадку призма
називається похилою.
Бічні
грані прямої призми — прямокутники,
висота прямої призми дорівнює бічному
ребру, діагональні перерізи є
прямокутниками.
Бічною
поверхнею призми
називається сума площ бічних граней.
Повна
поверхня призми
дорівнює сумі бічної поверхні й площ
основ.
Теорема 1. Бічна поверхня прямої
призми дорівнює добутку периметра
основи та висоти, тобто довжини бічного
ребра.
Перпендикулярним
перерізом призми
будемо називати переріз площиною,
перпендикулярною до бічного ребра
призми (а це означає, що ця площина є
перпендикулярною до всіх бічних ребер
призми).
Теорема 2. Бічна поверхня
похилої призми дорівнює добутку довжини
бічного ребра і периметра перпендикулярного
перерізу.
На рисунку
![]() —
перпендикулярний переріз.
Sб
= H
⋅
Pосн;
Sп
= Sб
+ 2Sосн.
Sб
= l
⋅
Pпер;
Sп
= Sб
+ 2Sосн.
—
перпендикулярний переріз.
Sб
= H
⋅
Pосн;
Sп
= Sб
+ 2Sосн.
Sб
= l
⋅
Pпер;
Sп
= Sб
+ 2Sосн.
 Очевидно,
що ця теорема є правильною й у випадку
прямої призми, бо тоді перпендикулярний
переріз буде перерізом площиною,
паралельною площинам основ призми.
Зверніть
увагу: якщо деякий многокутник є
перпендикулярним перерізом призми, то
його внутрішні кути є лінійними кутами
двогранних кутів між відповідними
бічними гранями.
У випадку прямої
призми лінійними кутами двогранних
кутів між бічними гранями є безпосередньо
кути основи.
Приклад
На
рисунку
—
пряма призма.
Очевидно,
що ця теорема є правильною й у випадку
прямої призми, бо тоді перпендикулярний
переріз буде перерізом площиною,
паралельною площинам основ призми.
Зверніть
увагу: якщо деякий многокутник є
перпендикулярним перерізом призми, то
його внутрішні кути є лінійними кутами
двогранних кутів між відповідними
бічними гранями.
У випадку прямої
призми лінійними кутами двогранних
кутів між бічними гранями є безпосередньо
кути основи.
Приклад
На
рисунку
—
пряма призма.

![]() —
лінійний кут двогранного кута між
гранями
—
лінійний кут двогранного кута між
гранями
![]() і
і
![]() .
Призма
називається правильною,
якщо:
• в основі її лежить правильний
многокутник;
• призма є прямою.
.
Призма
називається правильною,
якщо:
• в основі її лежить правильний
многокутник;
• призма є прямою.
