1. Проективное пространство.

Непустое множество  называется проективным пространством n измерений (порожденным векторным пространством ), если задано отображение , удовлетворяющее следующим аксиомам проективного пространства:

1) отображение f сюръективное (любому элементу из  соответствует хотя бы один вектор из )

2) равенство  выполняется тогда и только тогда, когда , то есть всем коллинеарным векторам  соответствует одна точка пространства .

Проекти́вное простра́нство над телом K — пространство, состоящее из прямых (одномерных подпространств) некоторого линейного пространства L(K) над данным телом. Прямые пространства L(K) называются точками проективного пространства.

Если L имеет размерность n + 1, то размерностью проективного пространства называется число n а само проективное пространство обозначается KPⁿ и называется ассоциированным с L (чтобы это указать, принято обозначение P(L)).

Переход от векторного пространства L(K) размерности n + 1 к соответствующему проективному пространству KPⁿ называется проективизацией пространства L(K).

Точки KPⁿ можно описывать с помощью однородных координат.

Если два треугольника расположены на плоскости таким образом, что прямые, соединяющие соответственные вершины треугольников, проходят через одну точку, то три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой.

Обратное тоже верно:

Если два треугольника расположены на плоскости таким образом, что три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой, то прямые, соединяющие соответственные вершины треугольников, проходят через одну точку.

Эти две теоремы являются двойственными по отношению друг к другу, и иногда объединяются в единую теорему, которая формулируется так: «Два треугольника имеют центр перспективы тогда и только тогда, когда они имеют ось перспективы».

2. Проективная плоскость и ее модели.

Проективная пло́скость — двумерное проективное пространство. Проективная плоскость отличается важной ролью, которую играет т. н. аксиома Дезарга, в проективных пространствах больших размерностей являющаяся теоремой.

Проективная плоскость над телом K это множество прямых (одномерных подпространств) трёхмерного линейного пространства K³. Данные прямые называются точками проективной плоскости. Проективная плоскость над телом K обычно обозначается KP², например , , и т. д..

3. Расширенная плоскость и ее свойства.

4. Проективная прямая и ее модели.

О пределение: Проективной прямой называется некоторое множество , для которой существует взаимнооднозначное отображение вида P₁→S, где S — пучок прямых вида плоскости и элементы множества Р₁ называется проективными точками.

Некоторые свойства проективной прямой:

1. Проективная прямая состоит из множества проективных точек.

2. Существует точка принадлежащая проективной прямой и точки не принадлежащие ей (т.к. существует другие п учки).

3. Порядок точки на Евклидовой прямой задается отношением лежать между.

На_проективной прямой такое отношение определять нельзя:

4. На проективной прямой порядок точки определяется отношением, который называется разделенность пар точек.

5. Расширенная прямая и ее свойства.

6. Координаты точки на проективной прямой.

7. Координаты точки на проективной плоскости.

8. Построение точки на проективной прямой по ее координатам.

9. Построение точки на проективной плоскости по ее координатам.

10. Принцип двойственности

В проективной геометрии на плоскости двойственными понятиями являются, «точка» и «прямая», «точка лежит на прямой» и «прямая проходит через точку». Каждой аксиоме в проективной геометрии на плоскости формулируется двойственное предложение, которое может быть доказано с помощью этих же аксиом (этим обосновывается Д. п. в проективной геометрии на плоскости)

11. Теорема Дезарга.

Теорема Дезарга является одной из основных теорем проективной геометрии. Она формулируется следующим образом:

Если два треугольника расположены на плоскости таким образом, что прямые, соединяющие соответственные вершины треугольников, проходят через одну точку, то три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой.

Обратное тоже верно:

Если два треугольника расположены на плоскости таким образом, что три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой, то прямые, соединяющие соответственные вершины треугольников, проходят через одну точку.

Эти две теоремы являются двойственными по отношению друг к другу, и иногда объединяются в единую теорему, которая формулируется так: «Два треугольника имеют центр перспективы тогда и только тогда, когда они имеют ось перспективы».

12. Порядок точек на проективной прямой.

На прямой в обычной евклидовой геометрии положение точек можно было характеризовать одним числом, одной координатой, отсчитываемой в некотором масштабе от точки, принятой за ноль. Так как в проективной геометрии бесконечно удаленная точка является равноправной с любой другой точкой, то уже невозможно одним числом представить координату этой бесконечно удаленной точки.

Здесь уже, на проективной прямой исходят из рассмотрения взаимного расположения двух пар точек.

Пусть A и B, C и D две пары точек, расположенные на проективной прямой (рис.5). Тогда чтобы совместить точку C с другой точкой своей пары, т.е. CD мы при движении ее по прямой обязательно встретимся в какой-то момент с т. A или т. B. Аналогично, чтобы совместить B с A, при движении точки B она когда-нибудь совпадет с C или D. В таком случае говорят, что пара точек A и B разделяет пару точек C и D. На этом основаны аксиомы порядка и введения координат на проективной прямой.

1. Каковы бы ни были три различные точки A, B, C произвольной прямой U, на этой прямой существует такая точка D, что пара A, B разделяет пару C, D.

2. Если пара A, B разделяет пару C, D; пара C, D разделяет пару A, B.

3. Каковы бы ни были четыре различные точки A, B, C, D прямой из них могут быть всегда единственным образом составлены две раздельные пары.

13. Двойное отношение четырех точек прямой. Свойства двойного отношения.

Двойным (или сложным) отношением четверки точек A, B, C, D, лежащих на одной (вещественной или комплексной) прямой, называют число

где через a, b, c, d обозначены координаты точек A, B, C, D соответственно.

Двойное отношение не зависит от выбора координаты на прямой. Часто пишут также так:

подразумевая, что через AC / BC (соответственно AD / BD) обозначено отношение направленных отрезков.

• Двойное отношение четверки точек на прямой сохраняется при проективных преобразованиях плоскости или пространства.

Двойным отношением четверки прямых a, b, c, d, проходящих через одну точку, называют число

знак которого выбирается следующим образом: если один из углов, образованных прямыми a и b, не пересекается ни с одной из прямых c или d (в этом случае говорят, что пара прямых a и b не разделяет пару прямых c и d), то (ab,cd) > 0; в противном случае (ab,cd) < 0.

• Двойное отношение сохраняется при дробно-линейных преобразованиях, в частности не зависит от выбора координат на прямой.

• 

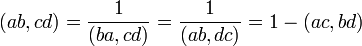
14. Гармонические четверки точек. Свойства гармонических четрверок

Введем обозначения: AB, CD (со стрелкой) – ненулевые коллинеарные векторы; AB, CD (с чертой)– их длины, взятые с одинаковыми знаками, если векторы сонаправлены, и с разными знаками, если они противоположно направлены. Тогда, в частности, выражения и будут представлять отношение и произведение, взятые со знаком «+», если векторы сонаправлены, и со знаком «–»,они противоположно направлены.

Воспользуемся принятыми обозначениями для определения гармонических четверок точек. Рассмотрим четыре точки А, В, С, D, лежащие на одной прямой. Будем говорить, что точки А, В, С, D (взятые в том же порядке, как указано) образуют гармоническую четверку, если (*)

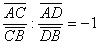Из равенства следует, что среди данных векторов три вектора сонаправлены, а четвертый вектор направлен противоположно по отношению к ним.

Отметим, что данное равенство равносильно каждому из следующих равенств:

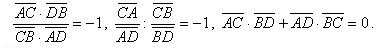
Можно написать еще несколько равенств, равносильных (*).