БИЛЕТ 10

1. Критерий планарности Понтрягина–Куратовского.

Для того чтобы сформулировать широко известный критерий Понтрягина–Куратовского, введем понятие гомеоморфизма графов. Нам понадобится операция подразбиения ребра e = ab графа. Она состоит в следующем: из графа удаляется ребро e и добавляются два новых ребра e₁ = av, e₂ = vb, где v — новая вершина.

Два графа называются гомеоморфными, если оба они могут быть получены из одного и того же графа подразбиением его ребер

Очевидно, что количество вершин степени 2 не влияет на планарность графа, т. е. если граф планарный, то любой граф, гомеоморфный ему, также является планарным.

Теорема 13.16. (Критерий Понтрягина – Куратовского). Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K₅ или K_3,3.

2. Формула включений и исключений.

Теорема 10.1. (формула включений и исключений).

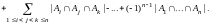(9)

 Каждый x элемент из 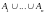дает единицу в 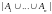. Покажем, что такой же вклад x вносит в правую часть равенства (9). Пусть, для определенности, x входит ровно в m множеств: . Тогда элемент x подсчитывается в правой части (9)

(10)

раз. Легко заметить, что из формулы бинома Ньютона для (a + b)ⁿ при a = 1 и b = –1 следует

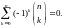
Используем его для преобразования выражения (10):



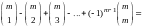
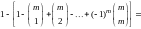
БИЛЕТ 11

1. Эйлеровы графы. Теорема Эйлера. Алгоритм Флери.

Цикл в графе называется эйлеровым, если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл, называется эйлеровым графом. Такой граф можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.

Теорема 14.1. (Л. Эйлер, 1736 г.). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.

 Необходимость. Пусть G — эйлеров граф. Эйлеров цикл этого графа, проходя через каждую его вершину, входит в нее по одному ребру, а выходит по другому. Это означает, что каждая вершина инцидентна четному числу ребер эйлерова цикла, а поскольку такой цикл содержит все ребра графа G, то отсюда следует четность степеней всех его вершин.

Достаточность. Предположим теперь, что степени вершин графа G четны. Начнем цепь P₁ из произвольной вершины v₁ и будем продолжать ее, насколько возможно выбирая каждый раз новое ребро. Так как степени всех вершин четны, то, попав в очередную отличную от v вершину, мы всегда будем иметь в распоряжении еще не пройденное ребро. Поэтому цепь P₁ можно продолжить путем добавления этого ребра. Таким образом, построение цепи P₁ закончится в вершине v₁, т. е. P₁ непременно будет циклом. Если окажется, что P₁ содержит все ребра графа G, то это будет требуемый эйлеров цикл. В противном случае, удалив из G все ребра цикла P₁, рассмотрим граф G₁, полученный в результате такой операции. Поскольку P₁ и G имели вершины только четных степеней, то, очевидно, и G₁ будет обладать тем же свойством. Кроме того, в силу связности графа G графы P₁ и G₁ должны иметь хотя бы одну общую вершину v₂. Теперь, начиная с вершины v₂, построим цикл P₂ в графе G₁ подобно тому, как строили цикл P₁. Обозначим через P₁‘ н P₁” части цикла P₁ от v₁ до v₂ и от v₂ до v₁ соответственно (см. рис. 14.2). Тогда получим новый цикл графа P₃ = P₁'  P₂  P₁”, который, начиная с v₁, проходит по ребрам цепи P₁‘ до v₂, затем обходит все ребра цикла P₂ и, наконец, возвращается в v₁ по ребрам цепи P₁” (рис. 14.2).

Если цикл P₃ не эйлеров, то проделав аналогичные построения, получим еще большой цикл и т. д. Этот процесс закончится построением эйлерова цикла. 

1. Начиная с произвольной вершины u, присваиваем произвольному ребру uv номер 1. Затем вычеркиваем ребро uv и переходим в вершину v.

2. Пусть w — вершина, в которую мы пришли в результате выполнения предыдущего шага, и k — номер, присвоенный некоторому ребру на этом шаге. Выбираем любое ребро, инцидентное вершине w, причем мост выбираем только в том случае, когда нет других возможностей; присваиваем выбранному ребру номер k + 1 и вычеркиваем его.

Этот процесс, называемый алгоритмом Флёри, заканчивается, когда все ребра графа вычеркнуты, т. е. занумерованы.

2. Число всех отображений, число сюръективных отображений конечных множеств (элементы в 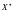неразличимы).

Утверждение 7.5. А. Число сюръективных отображений f : X*  Y (X* означает, что элементы X неразличимы) равно ;

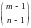Б. Число всех отображений f : X*  Y равно .

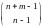 А). Так как f — сюръективное отображение, то справедливо

| f ^–1(y₁) | + | f ^–1(y₂) | + | f ^–1(y₃) | + . . . + | f ^–1(y_n) | = m ,

где | f^–1(y_i) | = a_i > 0, i = 1, 2,…, n, или a₁ + a₂ + … + a_n = m. Поставим в соответствие набору (a₁, a₂,…, a_n) двоичный вектор

(1)

Очевидно, что соответствие между векторами (1) и сюръективными отображениями f является биекцией (элементы X* неразличимы). Подсчет векторов (1) можно трактовать как подсчет расстановок n – 1 перегородок (нулей) на m – 1 место между m единицами (две перегородки не могут располагаться рядом из-за сюръективности f ). Ясно, что это можно сделать 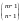способами.

Б). Если f не являться сюръекцией, то прообразы некоторых элементов yY могут не существовать, т. е. | f (y) | ^–1 = 0. Это значит, что в любой промежуток разрешается ставить любое количество перегородок. Подсчитаем число таких расстановок. В (1) имеется m – n + 1 мест для 1 и перегородок. Ставим на любые n –1 из них перегородки, а оставшиеся места автоматически заполняются 1. Число способов сделать это равно . 

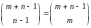БИЛЕТ 12