2. Определитель произвольного порядка.

Теперь можно ввести понятие определителя - го порядка.

Пусть – квадратная матрица х . Определителем матрицы называется число, равное следующему выражению:

(*)

В выражение для определителя входит ! слагаемых, каждое из которых соответствует некоторой подстановке 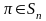. Знак перед слагаемым зависит от четности подстановки. Каждое слагаемое является произведением сомножителей: по одному из каждой строки и из каждого столбца.

Проверим согласованность с формулой (*) формул для вычисления определителей в случаях 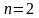и .

А). = 2. Имеем 2 перестановки: 1,2 и 2,1. Первая четная, вторая нечетная.

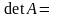
Б). = 3. Имеем 3! = 6 перестановок:

перестановка четность

1 2 3 +

1 3 2 -

2 1 3 -

2 3 1 +

3 1 2 +

3 2 1 -

.

Сопоставьте это с формулой, приведенной ранее.

2. Свойства определителя.

1). Если в матрице одна из строк нулевая (или один из столбцов нулевой), то 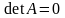. Доказательство очевидно, ведь в этом случае каждое слагаемое в формуле (*) равно 0.

2). Если две строки матрицы поменять местами (элементарное преобразование типа I), то определитель матрицы поменяет знак (кососимметричность). Иначе, пусть

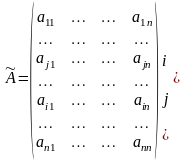
Тогда .

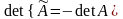Доказательство. Рассмотрим произвольное слагаемое в формуле (*) для матрицы , соответствующее подстановке , пока не учитывая его знак. Это слагаемое встретится и в разложении определителя 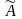, но будет соответствовать другой подстановке

: .

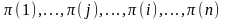Согласно лемме четность подстановок и различна, а значит, различны и знаки, с которыми эти слагаемые входят в соответствующие разложения определителей. Итак, при переходе от к все слагаемые в разложении (*) поменяют знаки, следовательно, изменит знак и определитель.

3). Если в матрице две одинаковые строки, то ее определитель равен нулю.

Доказательство моментально следует из предыдущего свойства. Если в такой матрице поменять местами две одинаковые строки, то определитель должен изменить знак. С другой стороны, он не изменится, так как не изменится и сама матрица. Значит, определитель равен нулю.

4). Пусть одна из строк матрицы представлена как сумма двух строк, т.е. матрица имеет вид

.

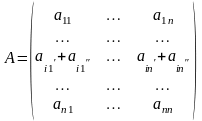Тогда 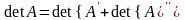, где

, .

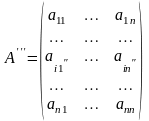Докажем это. По формуле (*)

=

+ .

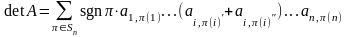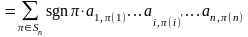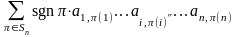
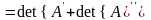5). Если одну из строк матрицы умножить на некоторое число 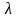, то определитель умножится на это же число . Действительно, если все элементы одной строки умножить на , то умножится на и каждое слагаемое в формуле (*), а значит, и определитель матрицы.

6). Если к одной строке матрицы прибавить другую строку, умноженную на какое-нибудь число (элементарное преобразование типа II), то определитель матрицы не изменится. Доказательство немедленно следует из предыдущих свойств. Пусть

.

Тогда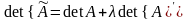 , где

-

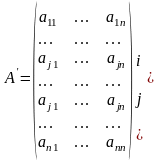матрица, у которой -я и -я строки совпадают, и следовательно, ее определитель равен нулю. Значит, .

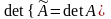7). При транспонировании матрицы определитель не меняется:

Докажем это. В разложении определителя (*) любое слагаемое с точностью до знака является произведением элементов матрицы по одному из каждой строки и из каждого столбца. Поэтому с точностью до знаков слагаемые в разложениях определителей исходной и транспонированной матриц совпадают. Теперь разберемся со знаками.

Возьмем произвольное слагаемое из разложения определителя матрицы и покажем, что в разложение определителя транспонированной матрицы оно будет входить с тем же знаком. Пусть это слагаемое соответствует подстановке π: . Упорядочим сомножители по второму индексу, т.е. по столбцам: , где 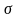– некоторая другая подстановка, причем 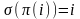. Заметим, что количество инверсий в перестановках 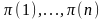и совпадает, ведь если выполнялось условие < , но > 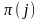, то после упорядочивания сомножителей по номерам столбцов появится соответствующая инверсия в перестановке номеров строк. Значит, четность подстановок и совпадает.

8). Из предыдущего свойства следует, что свойства 1)-6) справедливы не только для строк матрицы, но и для столбцов.

2. Разложение определителя по первой строке.

Заметим, что с увеличением размеров матрицы, т.е. с ростом , количество слагаемых в разложении (*) растет с огромной скоростью. При =4 оно равно 24, при =5 - 120, а при =6 - уже 720! Очевидно, что формула (*) едва ли пригодна для вычисления определителя при >3.

Выведем формулу, позволяющую свести вычисление определителя порядка к вычислению нескольких определителей порядка .

Сначала дадим

Определение. Минором 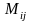называется определитель матрицы, получившейся из исходной вычеркиванием -й строки и -го столбца.

Теперь сформулируем и докажем следующую теорему.

Теорема 1 (о разложении определителя по первой строке). Справедлива формула:

. (**)

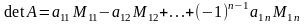Доказательство. Рассмотрим разложение (*). Разобьем сумму на группы слагаемых следующим образом: сначала соберем те произведения, которые содержат , потом те, которые содержат 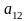и т.д. Получим

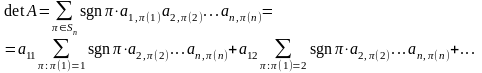
Заметим, что если есть перестановка , то - перестановка чисел от 1 до без числа . Число инверсий во второй перестановке на меньше чем в первой: так как число стояло на первом месте, то после него находилось чисел, меньших . После того, как убрали, эти инверсии исчезли. Остальные инверсии остались, новые появиться не могли.

Рассмотрим какую-нибудь группу слагаемых:

Все произведения элементов входят в разложение минора , но знак, с которым они входят в это разложение – в силу сделанного выше замечания – отличается на множитель 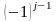. Таким образом, получаем требуемую формулу.

Дадим еще одно определение.

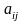Определение. Число называется алгебраическим дополнением элемента . Тогда формула (**) примет более изящный вид:

.
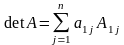