14. Взаимное расположение двух прямых. Нахождение точки пересечения, угла между прямыми. Условия параллельности и перпендикулярности прямых

Нахождение точки пересечения прямых

Пусть даны две прямые

и

Точка их пересечения удовлетворяет уравнениям обоих прямых. Получаем систему линейных уравнений.

(*)

По правилу Крамера:

; ;

Если , решение существует. Координаты точки пересечения

;

Если , а или , то решения нет, значит прямые – параллельные.

Если , то существует бесконечное множество решений, значит прямые совпадают.

Нахождение угла между прямыми

Пусть даны две прямые:

и

Условие параллельности

Условие перпендикулярности

[_]

15. Вывод канонического уравнения окружности

Пусть даны точка - центр окружности и ее радиус . Возьмем произвольную точку на плоскости - . Она принадлежит окружности тогда и только тогда когда расстояние от нее до центра равно радиусу , т.е. из билета №12

[_]

16. Эллипс: определение, каноническое уравнение, свойства

Определение

Эллипс – кривая на плоскости, для каждой точки которой сумма расстояний до 2-х фиксированных точек на плоскости , (фокусы) есть положительная постоянная величина ( ), большая, чем расстояние между фокусами ( ).

Каноническое уравнение

По определению эллипса

, (*)

Свойства

1. Эллипс симметричен относительно осей , . Если точка , то .

2. Исследуем форму эллипса при , . Из (*) получаем

Построим график последнего выражения

возрастает от до , убывает от до .

Следствие: эллипс находится в прямоугольнике

называется большой полуосью эллипса, - малой полуосью эллипса.

3. При (при этом ). Из (*) и

Получили уравнение окружности радиуса .

4. Эксцентриситет эллипса:

При - эллипс превращается в окружность.

При - эллипс вытягивается вдоль .

[_]

17. Гипербола: определение, каноническое уравнение, свойства

Определение

Гипербола – кривая на плоскости, для каждой точки которой модуль разности расстояний от двух фиксированных точек и (фокусов) есть положительная постоянная величина ( ) меньшая, чем расстояние между фокусами ( ).

Каноническое уравнение

, (*)

Свойства

1. Гипербола симметрична относительно осей , .

2. Исследуем форму гиперболы при и . Из (*)

При изменении от до , возрастает от до . При , точка гиперболы бесконечно приближается к прямой - к асимптоте гиперболы.

3. Построение гиперболы

1. Строится основной прямоугольник гиперболы

2. Продолжаем диагонали прямоугольника – получаем асимптоты: .

4. Эксцентриситет гиперболы .

Пусть фиксировано.

При гипербола вытягивается вдоль .

При гипербола вытягивается вдоль .

[_]

18. Парабола: определение, каноническое уравнение, свойства

Определение

Парабола – кривая на плоскости, для каждой точки которой расстояние до некоторой фиксированной точки плоскости (фокуса параболы) равно расстоянию до некоторой фиксированной прямой (директрисы параболы), которая не проходит через фокус параболы.

Каноническое уравнение

директрисе .

параболе

_(*)

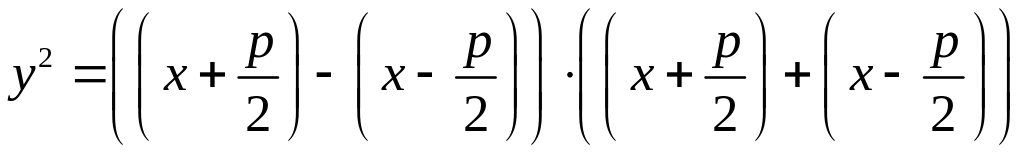
Свойства

1. Парабола симметрична относительно оси .

2. , значит парабола лежит в правой полуплоскости.

3. Начало координат (точка ) принадлежит параболе и является самой левой ее точкой.

4. Исследуем форму параболы при и . Из (*)

возрастает от до , возрастает от до .

[_]