9. Базис пространства векторов. Координаты вектора в базисе
Вектора
и
называются коллинеарными,
если
,
т.е. их представителей можно взять на
одной прямой.
Вектора , и называются компланарными, если их представителей можно взять на одной плоскости.
Базисом пространства
называется любая упорядоченная тройка
некомпланарных векторов
,
,
.
Базисом пространства называется любая упорядоченная пара неколлинеарных векторов.
Теорема
Любой вектор
(
)
раскладывается в линейную комбинацию
базисных векторов
(
):
(
)
(
)
Числа
(
)
называются координатами
вектора в базисе.
Доказательство:
Для :
Для :
(см. выше)
Подставляем, получаем:
Теорема
Координаты вектора в заданном базисе определены неоднозначно.
Операции над векторами в координатной форме
Пусть даны вектора
и
.
Тогда
Пусть дан вектор и число . Тогда
[_]
10. Скалярное произведение и его свойства
Пусть даны вектора
,
,
а
- угол между
и
.
Скалярным произведением
и
называется число
Корректность определения
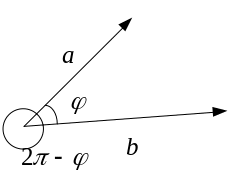
1.
2. Если
(либо
),
то
не определен, но
и
Свойства
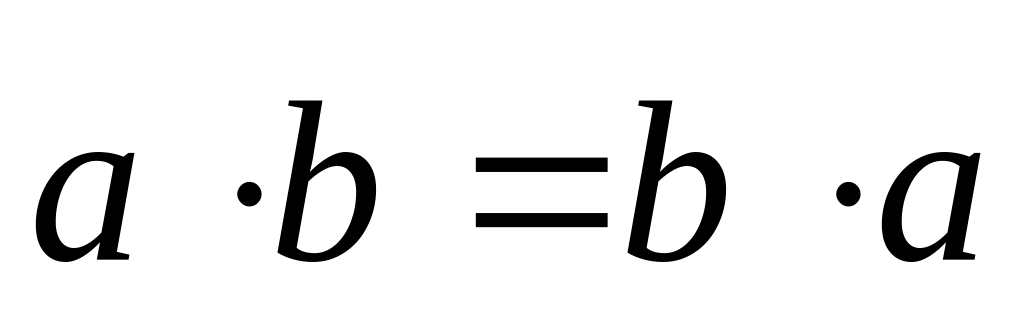
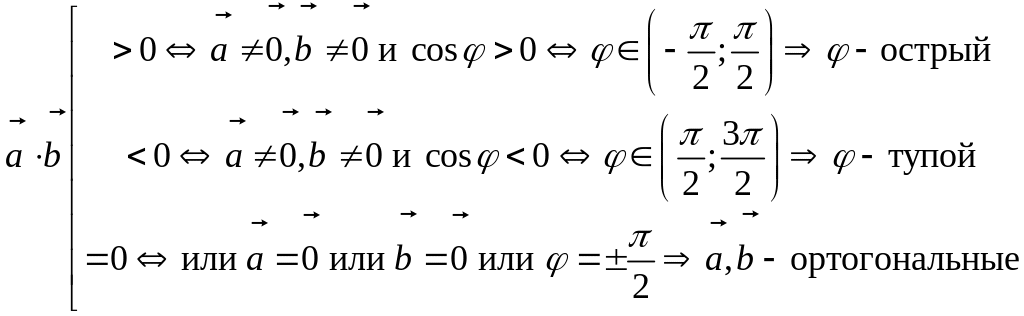
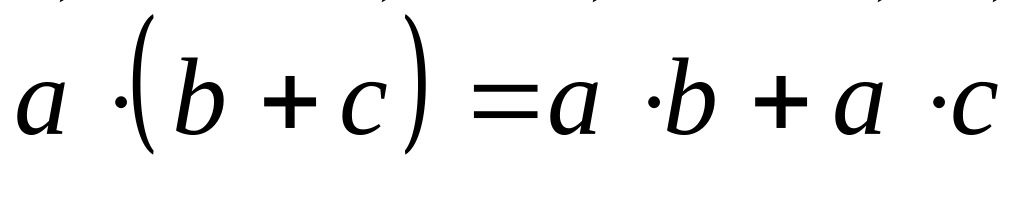
Для любого числа
Для любого
Если
и
,
то угол
[_]
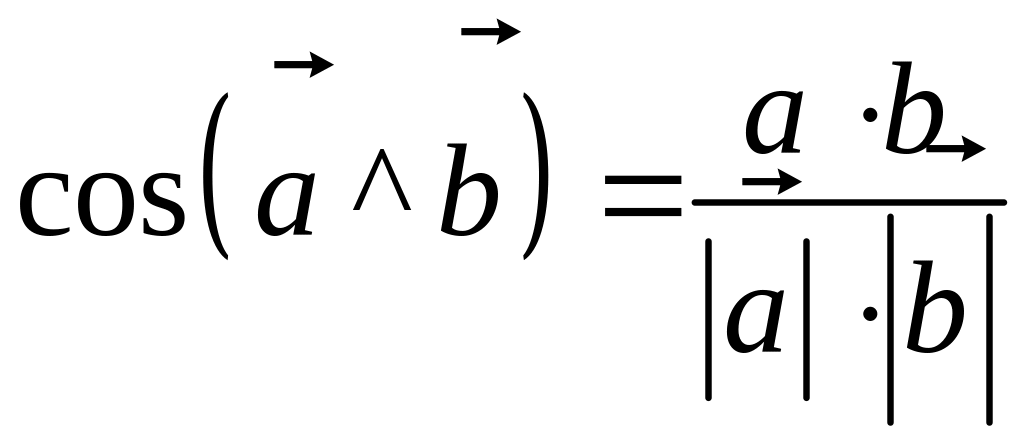
11. Ортонормированный базис. Скалярное произведение в ортонормированном базисе. Длина вектора, угол между векторами.
Ортонормированным базисом называется базис, в котором все базисные вектора перпендикулярны друг другу, а их модули равны 1:
,
,
,
,
,
Скалярное произведение
Обозначим
эти базисные вектора через
,
и
.
Имеем
,
,
(*)
(**)
Пусть даны векторы
,
С учетом (*) и (**) найдем
Длина вектора
Из билета №10
Угол между векторами
Из билета №10
[_]
12. Прямоугольная система координат в пространстве и на плоскости. Расстояние между двумя точками
Пусть
- произвольная точка пространства,
называемая началом координат.
Радиус-вектором точки
называется вектор, начало которого
совпадает с началом координат, а концом
является сама точка
.
Координаты точки
- это координаты ее радиус-вектора
.
Расстояние между двумя точками
Пусть даны две точки и . Проведем вектор . Тогда расстояние между этими точками будет равно длине этого вектора.
[_]
13. Различные формы уравнения прямой на плоскости
Общее уравнение прямой
при
(*)
Теорема
Общее уравнение первой степени от , (*) определяет на плоскости прямую.
Доказательство
1. Если
,
то (*)
,
,
- уравнение прямой.
2. При
,
(*)
- прямая
.
Неполное уравнение прямой
Неполное уравнение
– это когда в уравнении (*) один из
коэффициентов
,
или
равен 0.
1.
точка
принадлежит прямой, т.е. прямая проходит
через начало координат
2. - прямая .
3.
- прямая
.
Уравнение прямой
с угловым коэффициентом
Смысл
и
Пусть
,
тогда
,
т.е.
- смещение прямой по оси
относительно начала координат. Далее
из рисунка имеем
,
т.е. - тангенс угла наклона прямой.
Уравнение прямой,
с заданным угловым коэффициентом
и проходящей через точку
Уравнение прямой, проходящей через две заданные точки
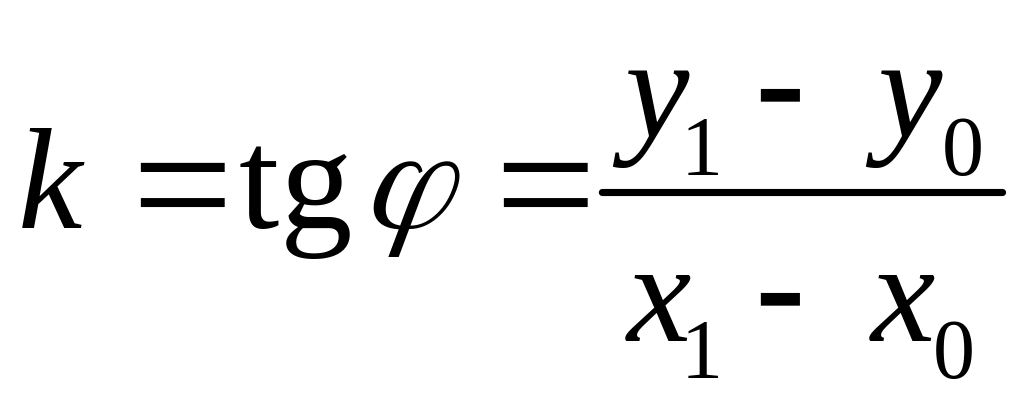
Воспользуемся
уравнением прямой с заданным угловым
коэффициентом и проходящей через точку
:
[_]
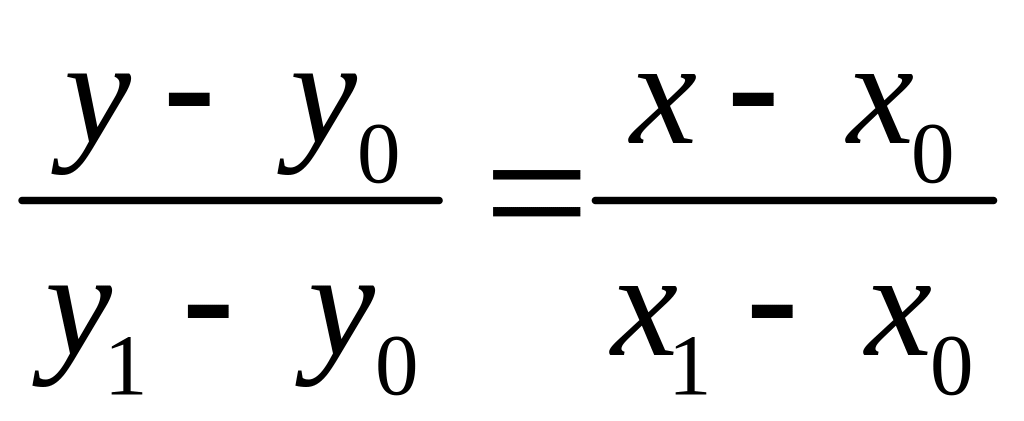