1. Решение систем линейных уравнений методом Гаусса
Общий вид системы линейного уравнения из 3-х уравнений с 3 неизвестными:
(*)
,
,
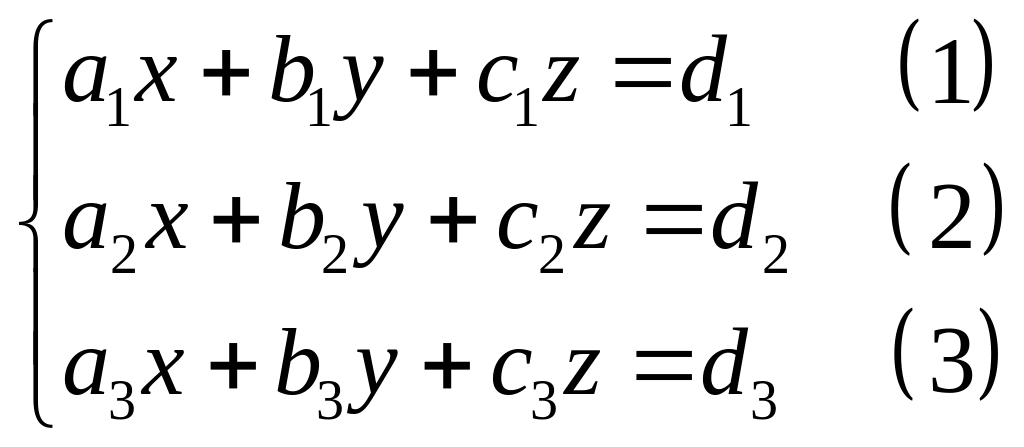называются переменными,
,
,
- коэффициентами,
- свободными членами.
Для решения такой системы уравнений можно использовать, например, метод Гаусса.
Метод Гаусса
Рассмотрим (*). Пусть
.
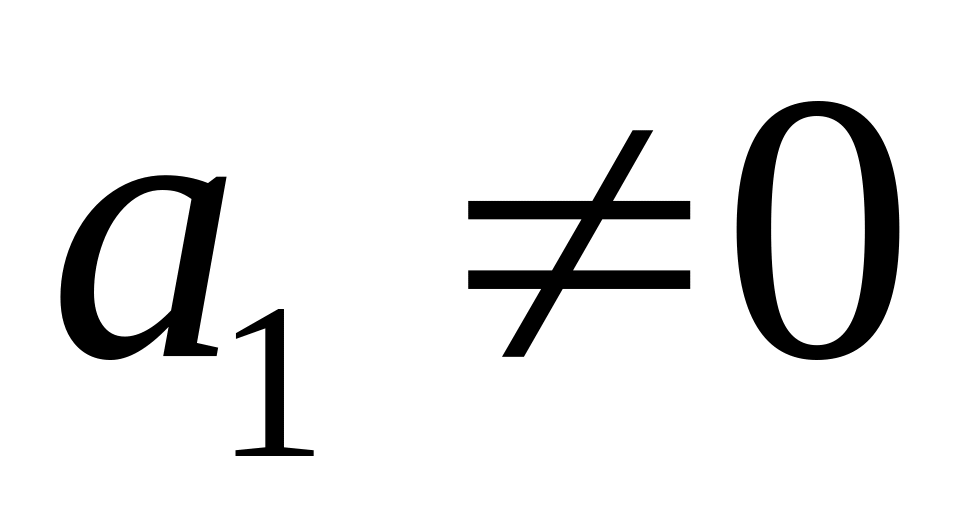Тогда исключим
из уравнений (2) и (3). Для этого:вычтем из строки (2) строку (1), помноженную на
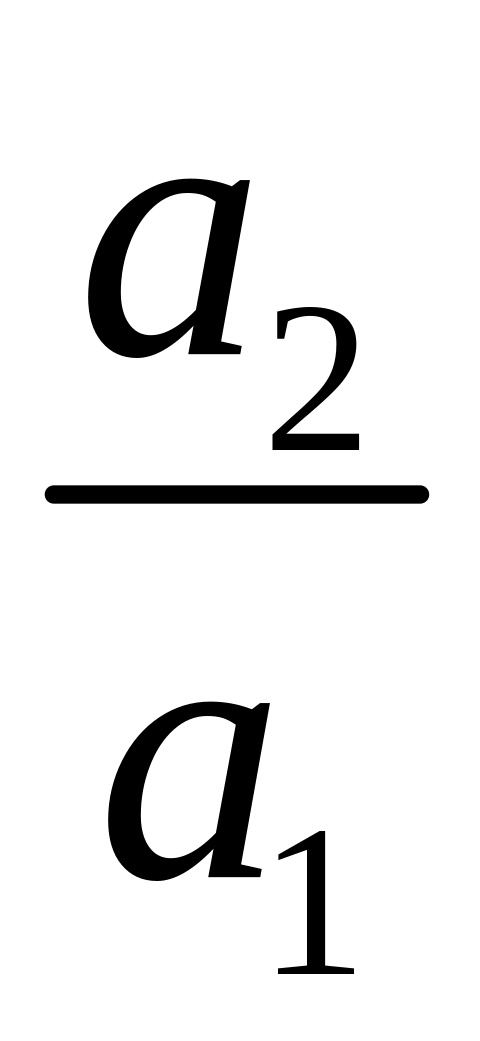;вычтем из строки (3) строку (1), помноженную на
.
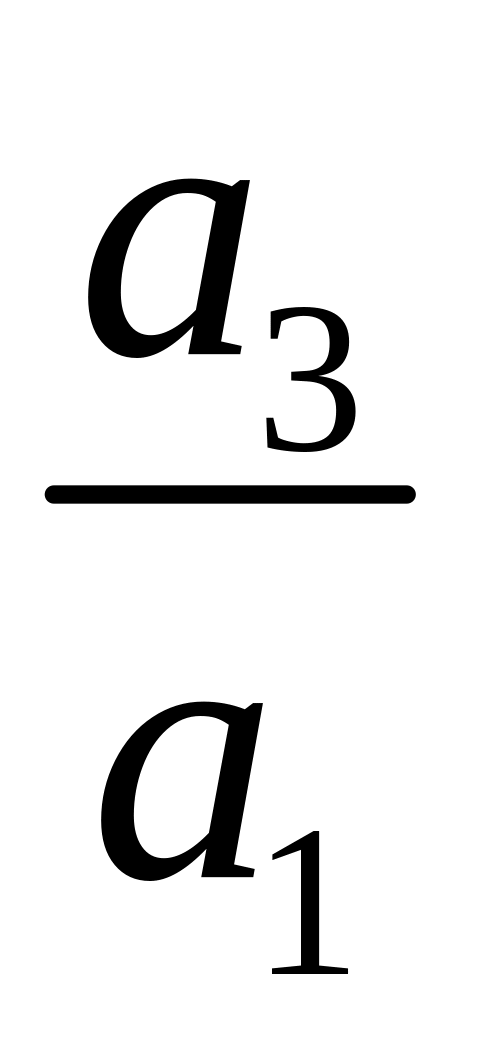Получим систему вида:
(**)
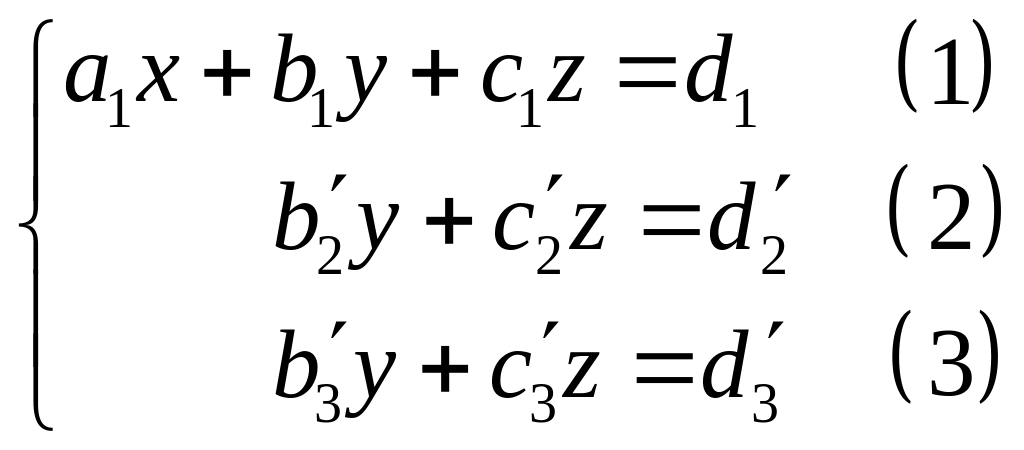Рассмотрим (**). Пусть
.
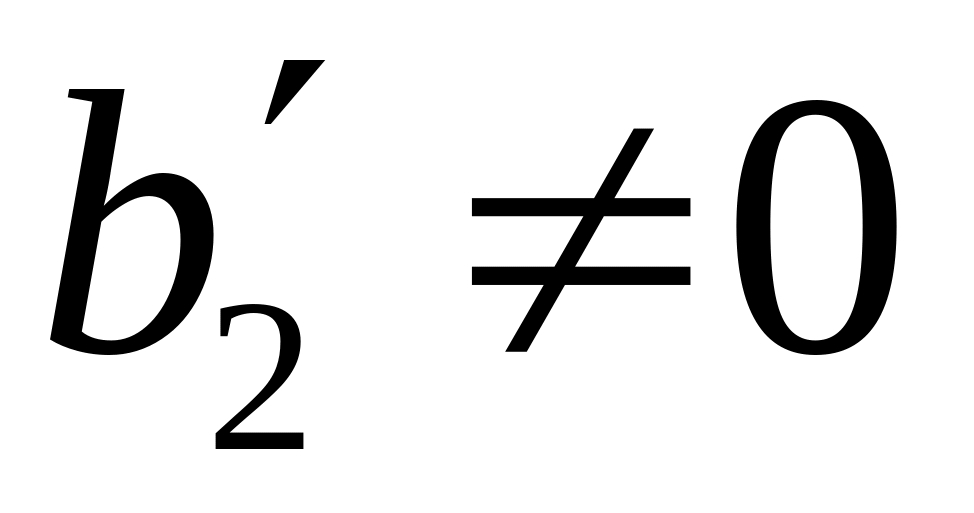Тогда исключим
из уравнения (3). Для этого вычтем из
строки (3) строку (2), помноженную на
.
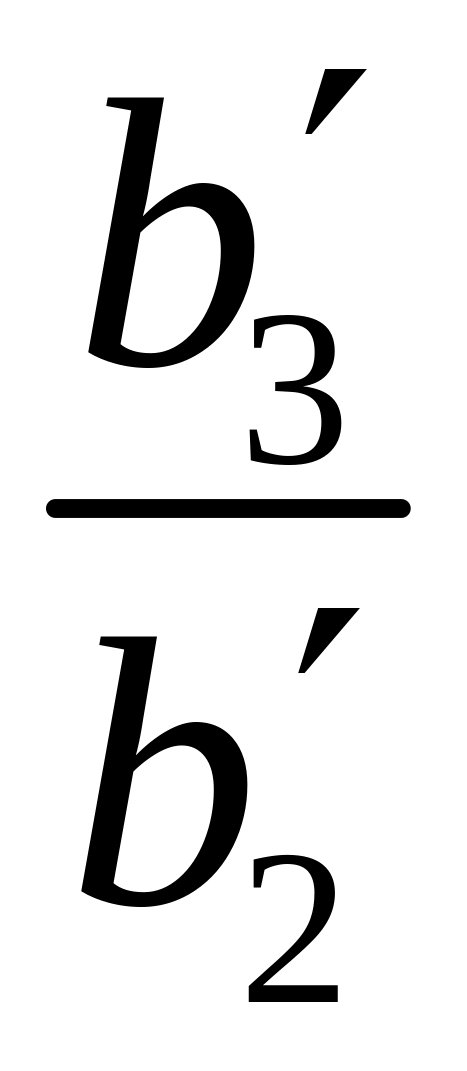Получим один из четырех видов системы:
1.
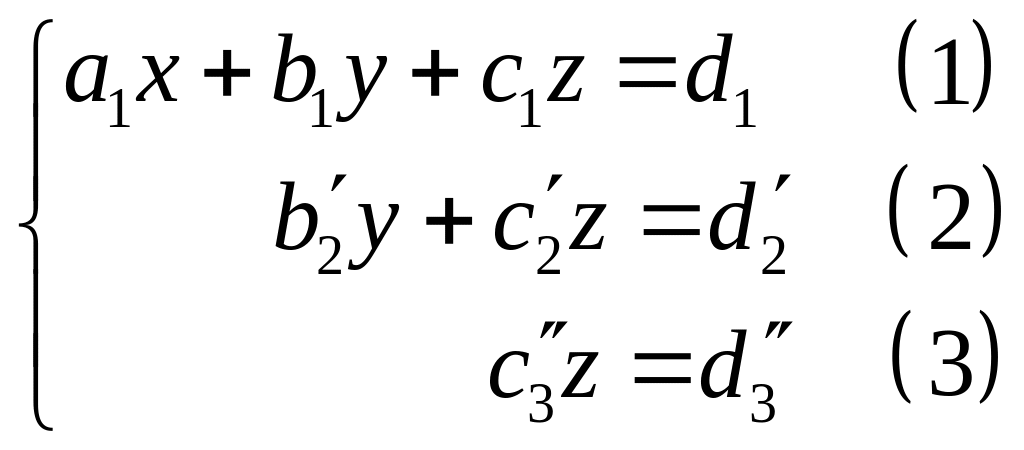
Пусть
.
Получаем решение:
;
;
.
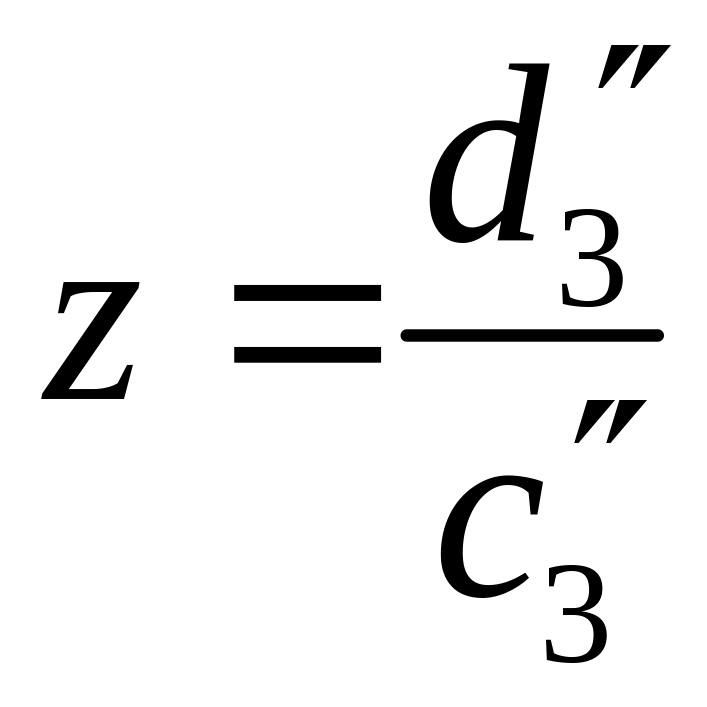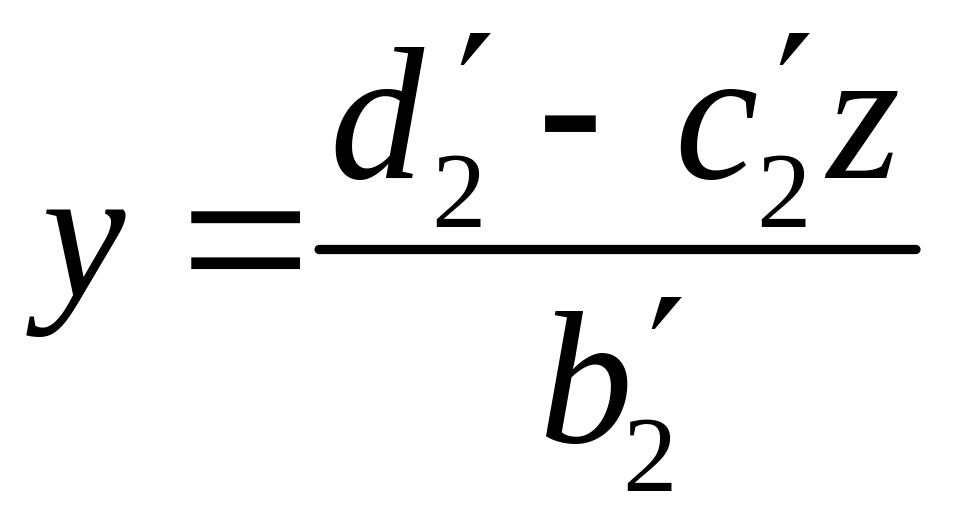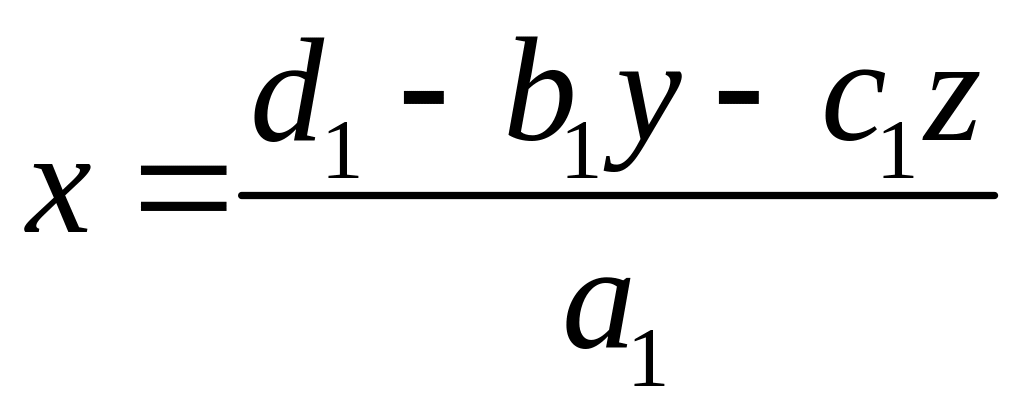2.
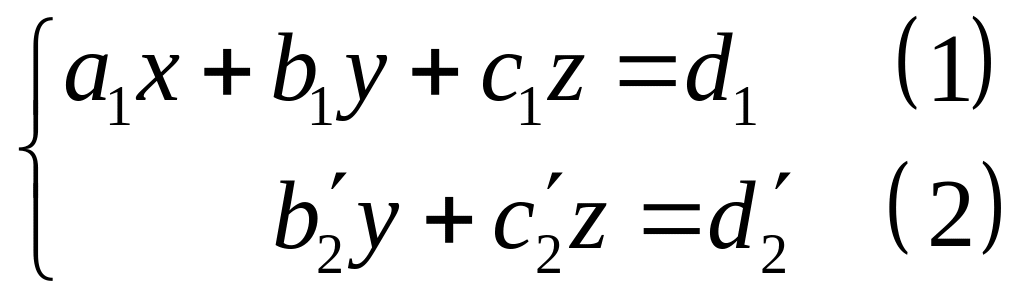
Система имеет бесконечное множество решений. Главные неизвестные: , , свободные - .
Присваиваем свободной
переменной любое постоянное значение:
.
Тогда
;
.
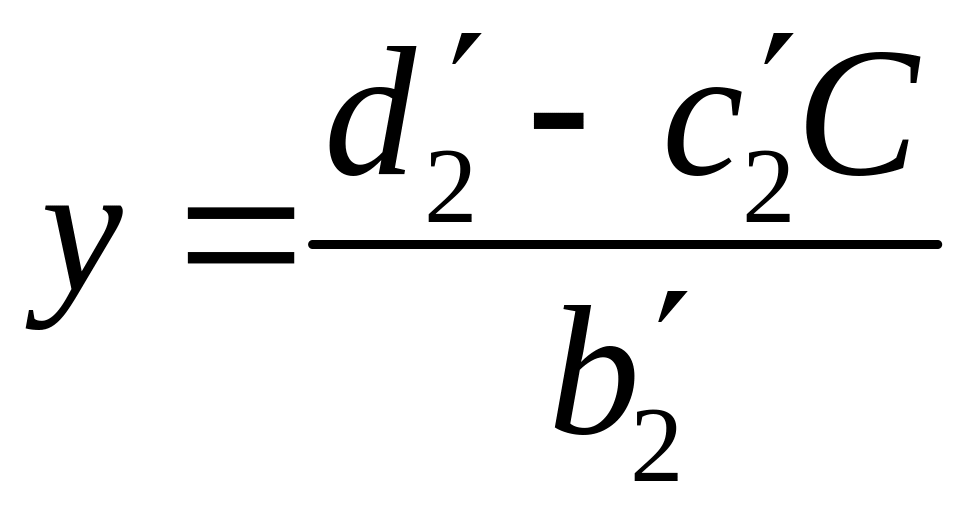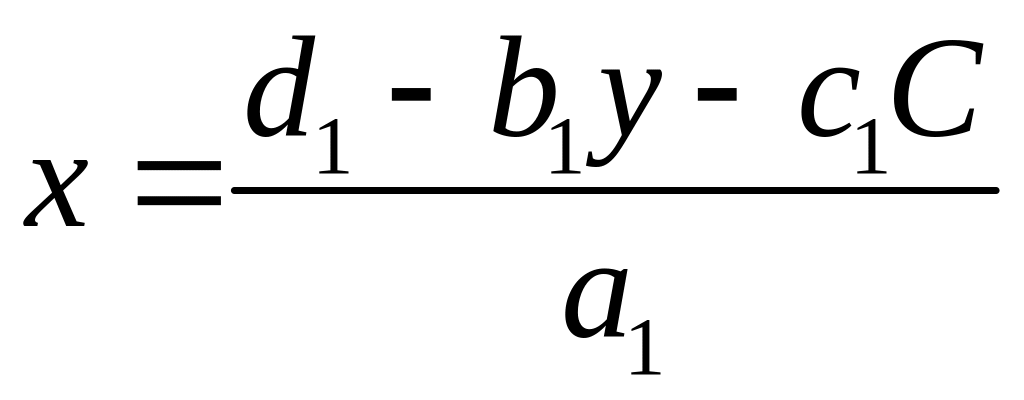3.
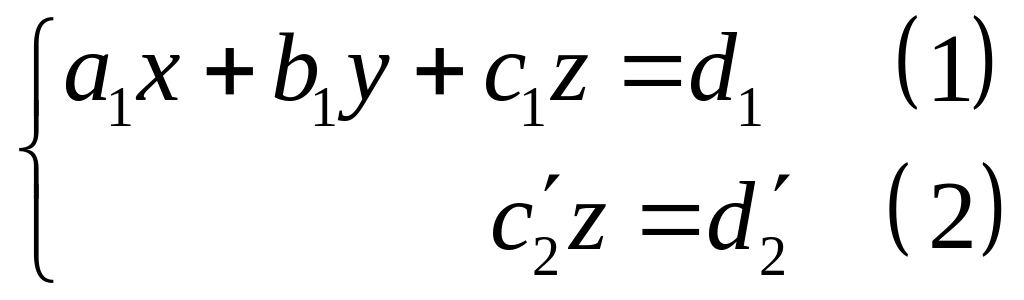
Система имеет бесконечное множество решений. Главные неизвестные: , , свободные - .
Присваиваем свободной
переменной любое постоянное значение:
.
Пусть
.
Тогда
;
.
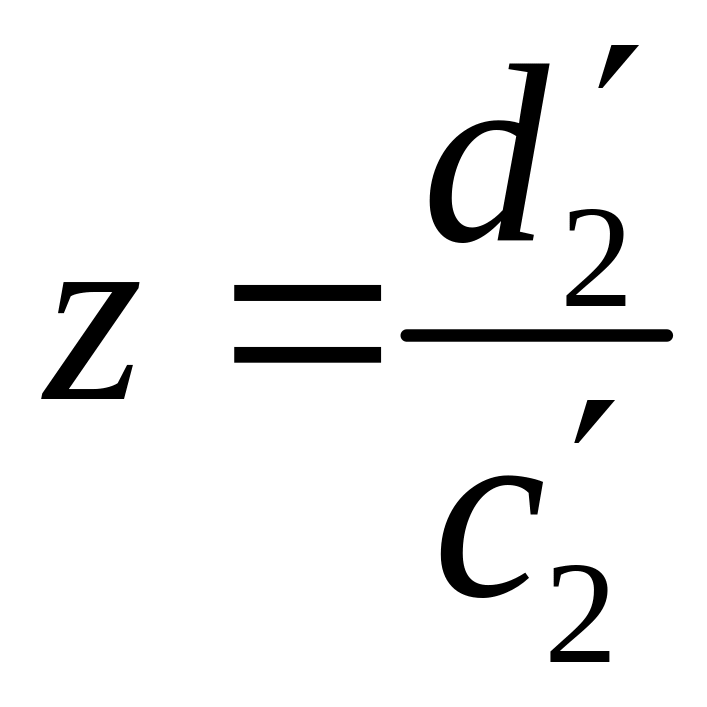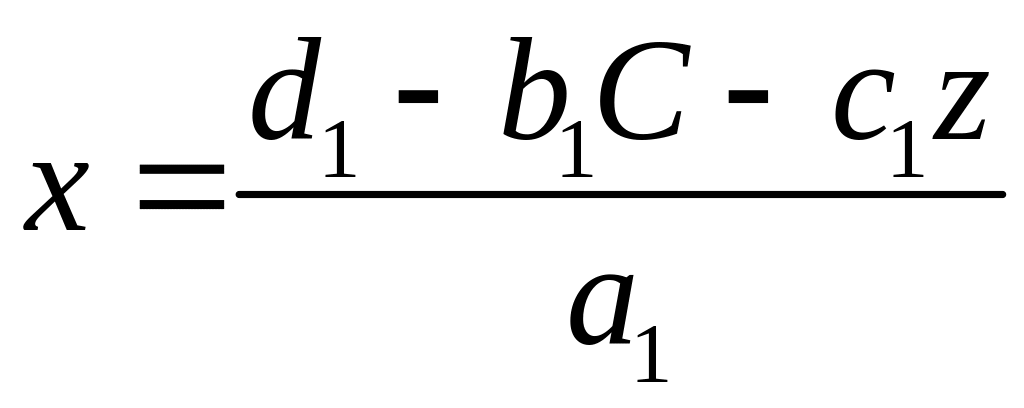4.
Система имеет бесконечное множество решений. Главные неизвестные: , свободные - , .
Присваиваем свободным
переменным любые различные постоянные
значения:
,
.
Тогда
.
[_]
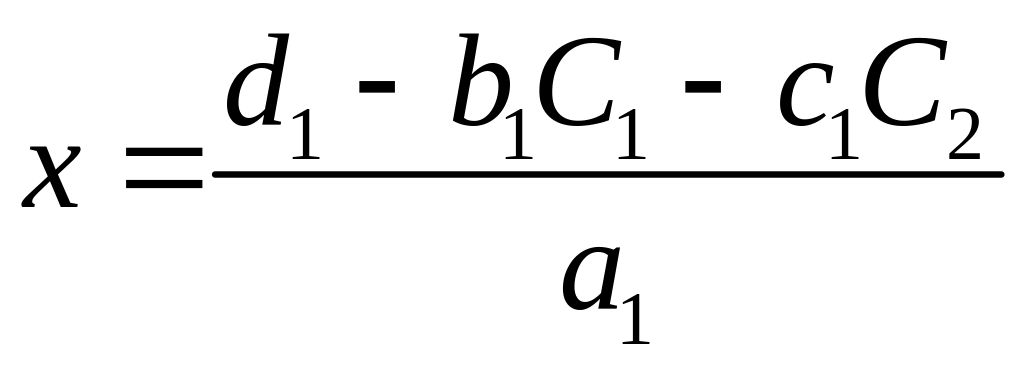2. Матрицы. Равенство матриц. Операции над матрицами: транспонирование, сложение, умножение на число, произведение матриц
Матрица
размером
(
- строки,
- столбцы) – это таблица
,
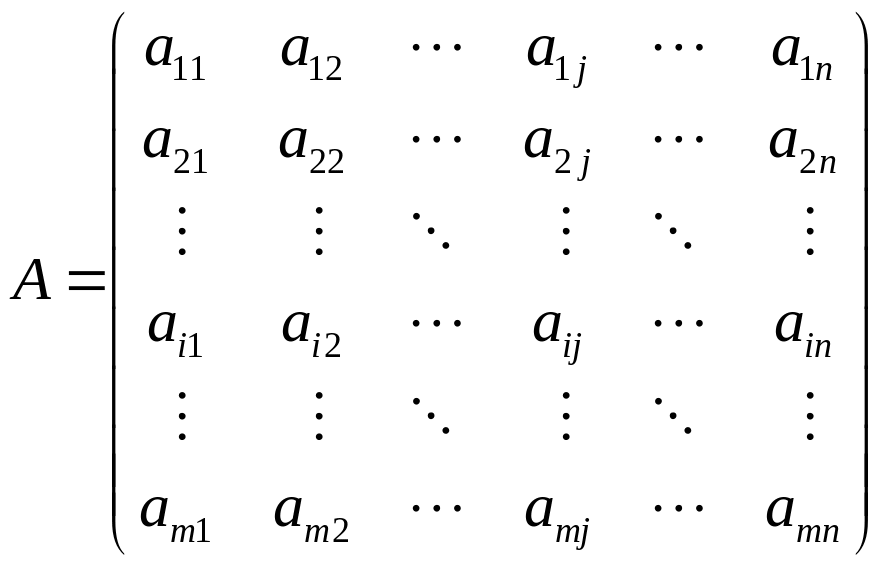Сокращенно
Равенство матриц
Пусть
,
.
Тогда
,
и
.
То есть матрицы равны, когда число строк,
столбцов и каждый элемент одной матрицы
равен числу строк, столбцов и каждому
элементу другой матрицы соответственно.
Транспонирование матриц
Транспонирование матрицы
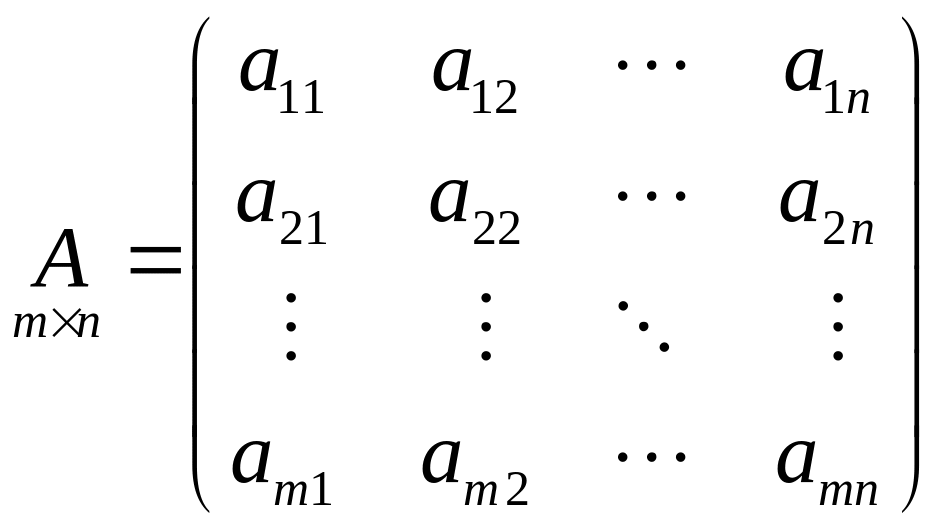
это переход к матрице
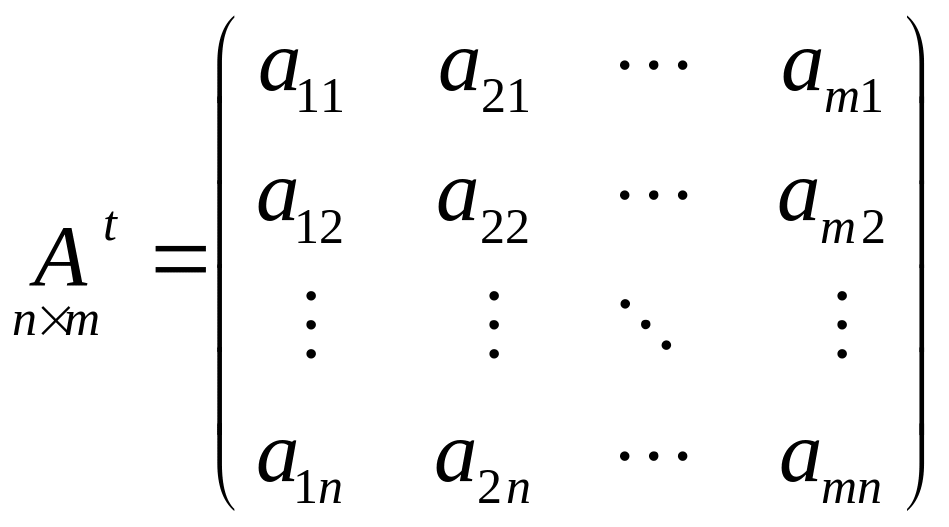
Пример
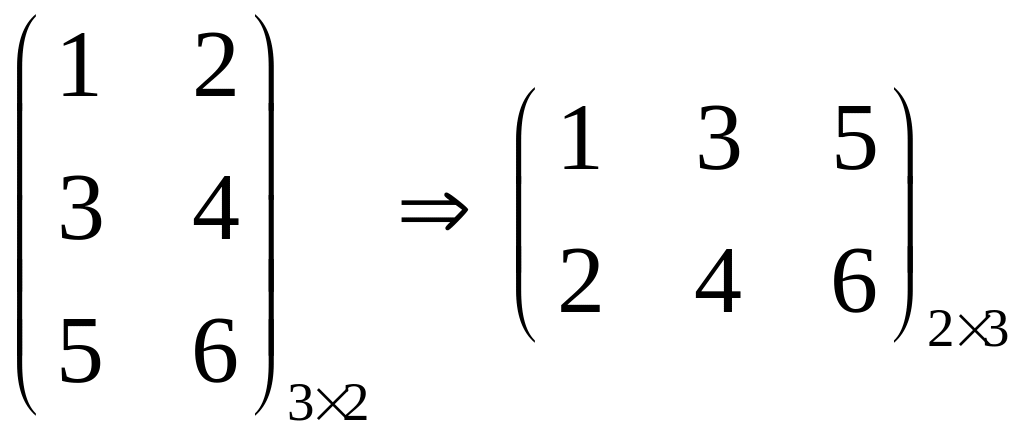
Свойство транспонирования:
Сложение матриц
Пусть даны две матрицы
;
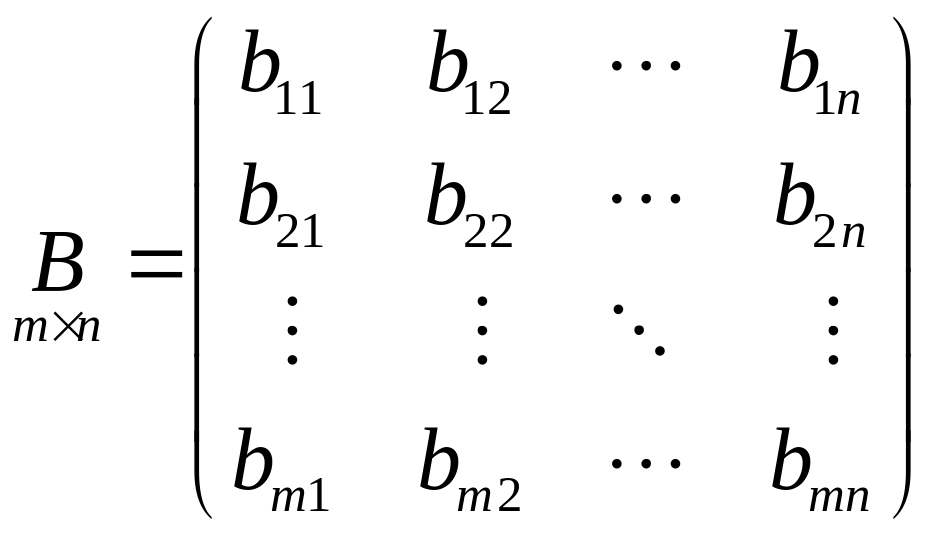
Тогда их суммой называется матрица
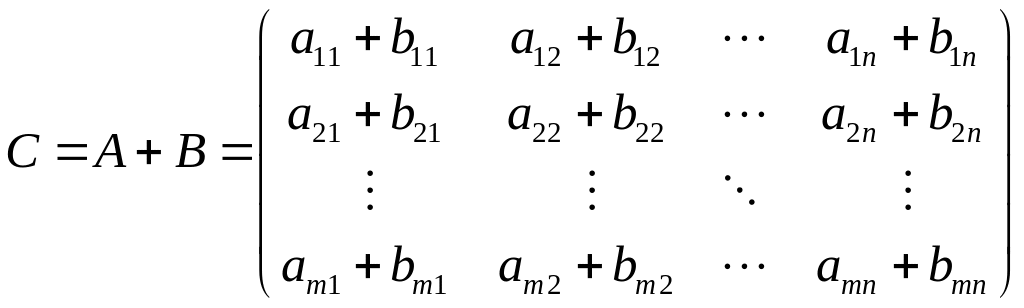
То есть
.
Умножение на число
Пусть дана матрица
Произведением
матрицы
на число
является матрица
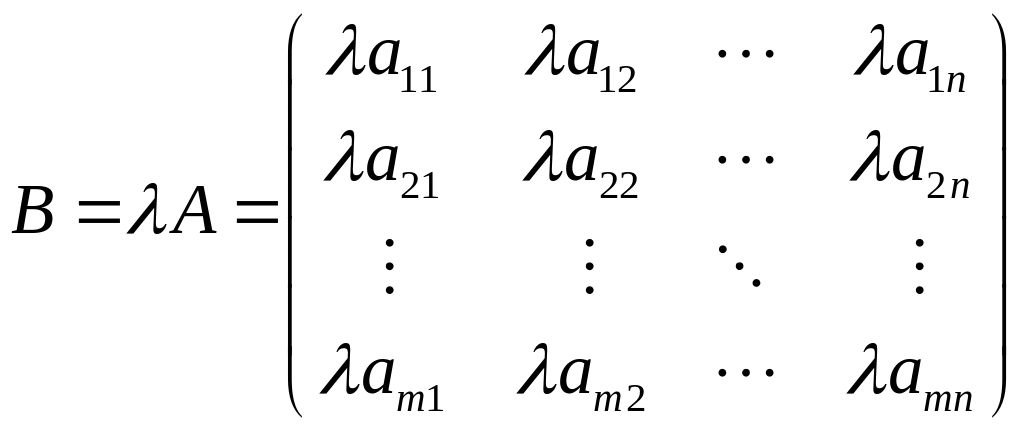
То есть
.
Умножение матриц
Пусть даны матрицы
и
(т.е. число столбцов первой матрицы равно
числу строк второй матрицы). Тогда
произведением этих матриц называется
матрица
,
где
,
т.е. произведение
-ой
строки матрицы
на
-ый
столбец матрицы
.
[_]
3. Определители 2-ого и 3-его порядков: их определения и свойства
Пусть дана квадратная матрица порядка .
:
.
:
.
:
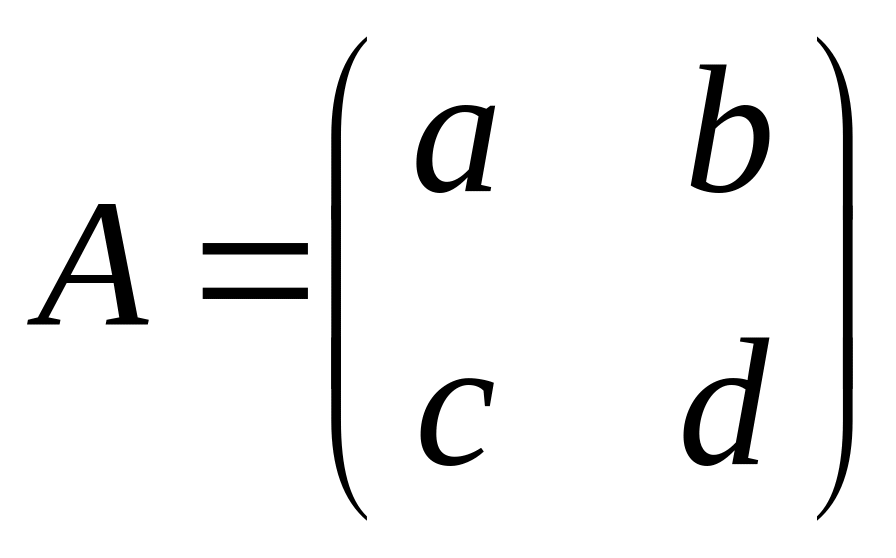
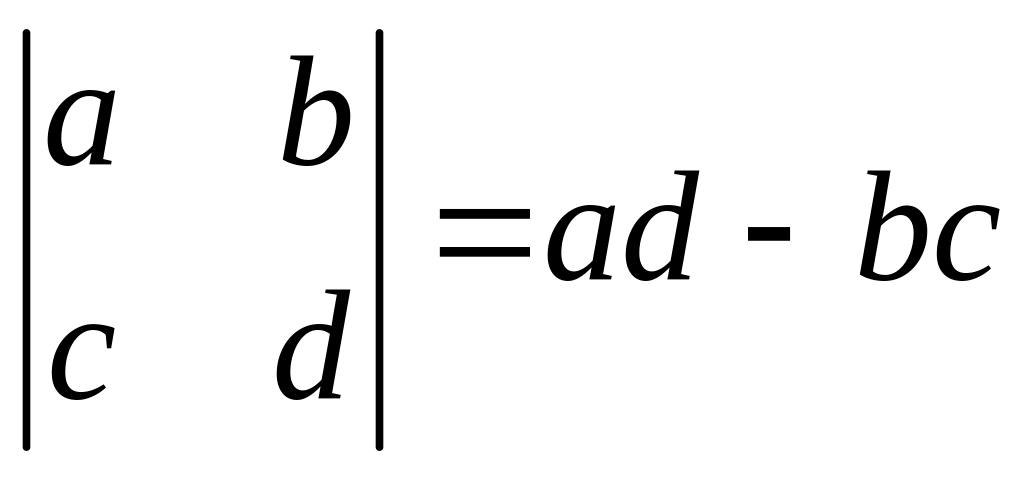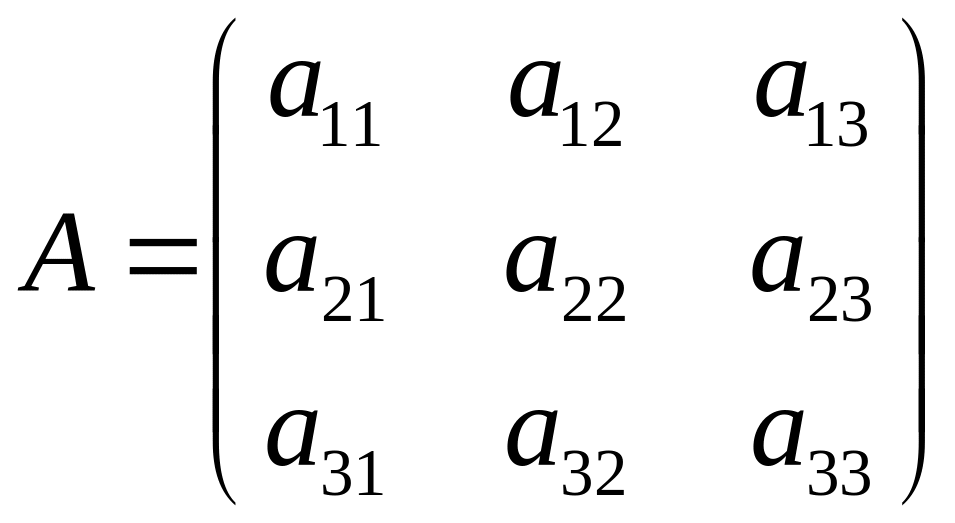
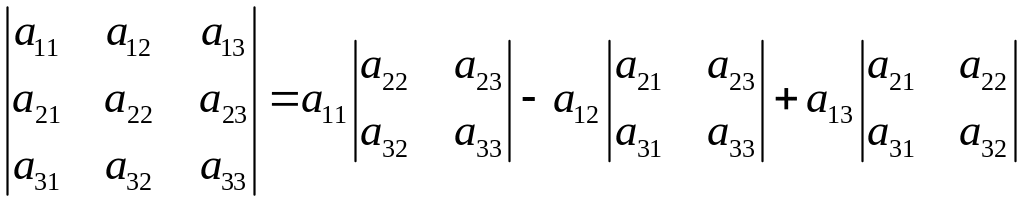
Свойства
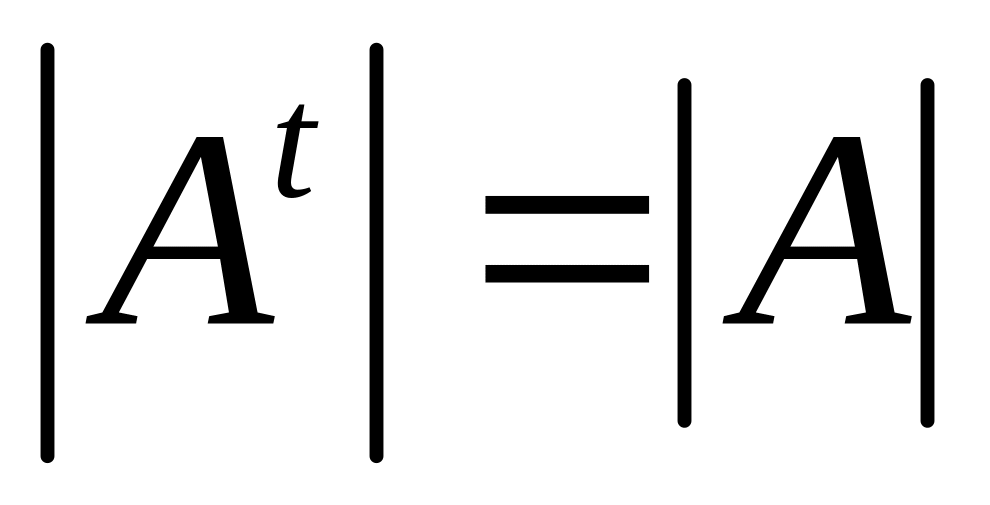
При перестановке двух строк местами меняется только знак определителя (на противоположный).
При прибавлении к строке другой строки, помноженной на произвольное число, определитель не меняется.
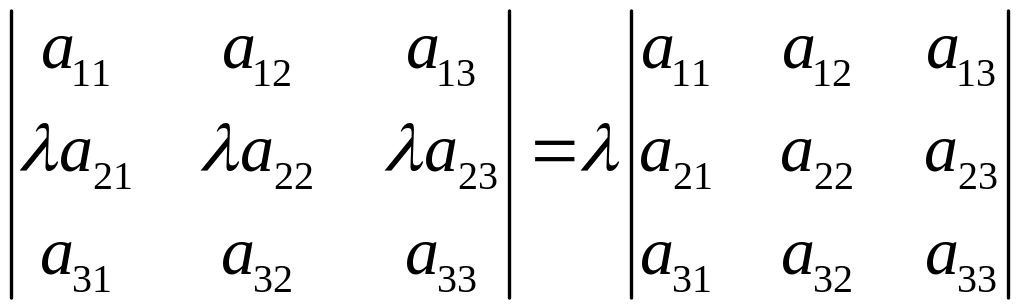
Следствие:
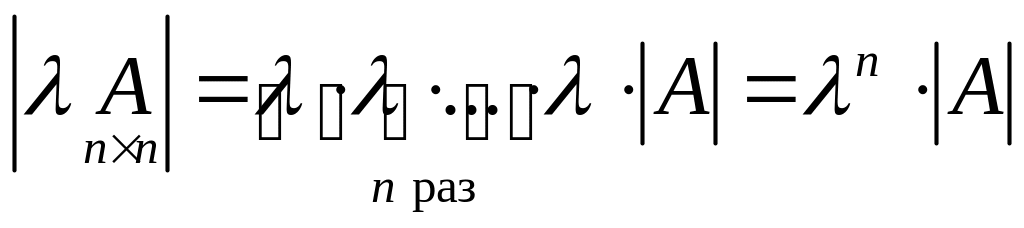
Определитель матрицы, содержащей строку, состоящую из нулей, равен 0.
Следствие: Определитель с двумя равными или пропорциональными строками равен 0, так как с помощью элементарных преобразований можно получить нулевую строку.
Определитель произведения матриц:
[_]