
- •Теория Вероятностей
- •Теорема 3. Монотонность вероятности.
- •Теоремы умножения вероятностей
- •Теорема умножения для зависимых событий
- •Функция распределения случайной величины, ее свойства.
- •Проверка гипотезы о нормальном распределении генеральной совокупности. Критерия согласия Пирсона.
- •Выборочный коэффициент корреляции r
- •Раздел3
Проверка гипотезы о нормальном распределении генеральной совокупности. Критерия согласия Пирсона.
Критерием согласия называется критерий проверки гипотезы о предлагаемом законе распределения.
Критерий согласия Пирсона (критерий проверки гипотезы о нормальном распределении генеральной совокупности):
1) По выборке объема n построить статический ряд:
2) Вычислить по таблице оценку математического ожидания и выборочное среднее квадратическое ожидание σв.
3)
В предположении нормального распределения
генеральной совокупности вычислить
теоретические частоты m1
теор,…,ml
теор
по формуле: mi
теор.=npi,
где
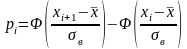 ,
Ф(х) – интегральная функция распределения
Лапласа.
,
Ф(х) – интегральная функция распределения
Лапласа.
4)
Вычислить число
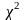 по формуле:
по формуле:
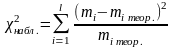 или
или

5)
По табл. 5 приложения найти число
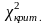 ,
учитывая заданный уровень значимости
α и число степеней свободы k=l-3.
,
учитывая заданный уровень значимости
α и число степеней свободы k=l-3.
6)
Сравнить число
 и
:
и
:
если < , то нет основания отвергать гипотезу о нормальном распределении генеральной совокупности;
если > , то гипотезу о нормальном распределении генеральной совокупности следует отвергнуть.
Корреляционная зависимость. Нахождение параметров уравнения линейной регрессии методом наименьших квадратов. Выборочно я коэффициент корреляции, его свойства.
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.
Корреляция в математической статистике, вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия.
Метод наименьших квадратов применяется для нахождения оценок неизвестных параметров функциональной зависимости y=f{x), вид которой предполагается известным. Пусть на опыте получено k пар результатов измерений (хi, уi), где i=l, 2,..., k. Предположим, что зависимость между X и Y близка к линейной. В этом случае естественно искать зависимость у=ах+b.
Рассмотрим оценку по методу наименьших квадратов параметров а и b.Из условия минимума суммы
![]()
эти оценки вычисляют по формулам:
(4.5)
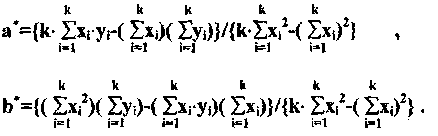 (4.6)
(4.6)
Если
предположить, что
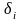 независимы, М(
)=0,
D(
)=
независимы, М(
)=0,
D(
)=
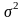 и полагая
и полагая
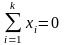 ,
можно
показать, что оценки
параметров а и b
линейной регрессии, полученные методом
наименьших квадратов, определяют по
формулам:
,
можно
показать, что оценки
параметров а и b
линейной регрессии, полученные методом
наименьших квадратов, определяют по
формулам:
![]()
Из этих равенств следует, что
![]()
Таким
образом, оценки а*,b*
являются несмещенными оценками параметров
а и b.
Оценки а* и b*
состоятельны, если
 при
k
->оо, так как в этом случае D(a*)-»0,
D(b*)-»0.
при
k
->оо, так как в этом случае D(a*)-»0,
D(b*)-»0.
Выборочный коэффициент корреляции r
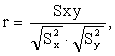 где
где
![]()
![]() ,
,
![]()
Выборочный
коэффициент корреляции r
является оценкой коэффициента корреляции
 генеральной
совокупности
и поэтому служит для измерения линейной
связи между величинами – количественными
признаками Y
и X.
генеральной
совокупности
и поэтому служит для измерения линейной
связи между величинами – количественными
признаками Y
и X.
r имеет свойства 1,3 коэффициента r, что позволяет использовать его как меру линейной связи между х и у:
1)
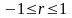
3) r = 1 тогда и только тогда, когда между x и y существует линейная зависимость.
В
самом деле, если r = 1, то дискриминант
трехчлена f(a) равен нулю, и существует
единственный корень уравнения f(a) = 0,
обозначим его ао. Тогда
![]() ,
выражение под знаком математического
ожидания равно нулю, то есть
,
выражение под знаком математического
ожидания равно нулю, то есть
![]() или
или
![]() .
.
Обратно,
если y
линейно выражается через x:
![]()
![]()
