Теоремы умножения вероятностей

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Пример 5: пусть А - из урны вытянули белый шар, B - из урны вытянули белый шар, тогда АВ - из урны вытянули два белых шара; если А - идет дождь, B - идет снег, то АB - дождь со снегом; А - число четное, B - число кратное 3, тогда АB- число кратное 6.

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В.

Два события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события А и В называются зависимыми. Например, из одной колоды тянут карты, не возвращая их.

Условной вероятностью P_A(B) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Теорема умножения для зависимых событий

Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: 

P (AB) = P (A)*PA(B).

(2.4)

Пример 6. В читальном зале имеется 6 учебников по информатике, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.

Решение. Рассмотрим следующие события:  А1- первый взятый учебник в переплете;  A2- второй взятый учебник в переплете.

Событие A = A₁ * A₂, состоит в том, что оба взятых учебника в переплете. События А₁ и А₂ являются зависимыми, так как вероятность наступления события А₂ зависит от наступления события А₁. Поэтому, для вычисления вероятности воспользуемся формулой (2.4).

Вероятность наступления события А₁ в соответствии с классическим определением вероятности:

P (А₁) = m / n = 3/6 = 0,5.

P _А1 (А₂) определяется как условная вероятность наступления события А₂ при условии, что событие А₁ уже наступило:

P _А1 (А₂) = 2/5 = 0,4.

Тогда искомая вероятность наступления события А:

P (А) = 0,5 * 0,4 = 0,2.

Теорема умножения для независимых событий

Теорема. Вероятность произведения двух независимых событий А и В равна произведению их вероятностей: 

P(AB) = P(A)*P(B).

(2.5)

Теорема сложения вероятностей совместных событий

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример 6. А - появление четырех очков при бросании игральной кости; В - появление четного числа очков. Событие А и В - совместны.

Теорема. Вероятность появления хотя бы одного из двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их совместного появления: 

P (A + B) = P (A) + P (B) - P (AB).

(2.6)

Пример 7. Два студента читают книгу. Первый студент дочитает книгу с вероятностью – 0,6; второй – 0,8. Найти вероятность того, что книга будет прочитана хотя бы одним из студентов.

Решение. Вероятность того, что книга будет прочитана каждым из студентов не зависит от результата отдельно взятого студента, поэтому события А (первый студент дочитал книгу) и B (второй студент дочитал книгу) независимы и совместны. Искомую вероятность находим по формуле 2.6.

Вероятность события АB (оба студента дочитали книгу):

P (AB) = P (A) * P (B) = 0,6 * 0,8 = 0,48.

Тогда

P (A + B) = 0,6 + 0,8 - 0,48 = 0,92.

Формула полной вероятности

Теорема. Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B₁, B₂,…, B_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A: 

(2.7)

Вероятность гипотез. Формулы Байеса

Теорема. Если существуют n попарно несовместных событий B₁, B₂,…, B_n, образующих полную группу, и известны условные вероятности события А, то можно найти вероятности того, что событие А произошло при условии появления некоторого события B_i по формуле: 

.

(2.8)

Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

• Вероятность противоположного события: Событие, противоположное событию A, обозначается как 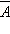  и состоит в том, что в результате испытания A не произошло. Например, в нашем случае 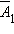  значит, что на кубике A выпало число, не равное 1. Сумма вероятностей события и его отрицания есть достоверное событие, то есть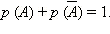 

(Док-во): Выпишем все возможные результаты броска кубика A: A₁, A₂, A₃, A₄, A₅, A₆. В этом случае общее число равновероятных вариантов N = 6, при этом   встречается   раз, «не 1» –   

Значит,   

Вообще, поскольку все возможные варианты заключаются либо в событии A, либо в событии «не A», то 

• Монотонность вероятности:

• Вероятность объединения нескольких несовместных событий:

P(A + B) = P(A) + P(B) - вероятность наступления в результате эксперимента хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий.  Обсуждение. Напомним, что события А и В называются несовместными, если в результате опыта они не могут появиться вместе. (Пожалуйста, не путайте их с независимыми событиями, которые мы обсуждали в прошлом разделе. Независимые события могут спокойно сосуществовать друг с другом.)

• Вероятность суммы двух совместных событий:

Теорема (вероятность суммы совместных событий). Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ).

• Классическая модель вероятности и классическая формула вероятности:Вероятностью случайного события А в данном испытании называется число, обозначаемое p(A) и вычисляемое по формуле: p(a)=m/n, где n – число всех возможных элементарных событий рассматриваемого испытания, m- число тех элементарных событий из всех возможных, которое благоприятствуют появлению события А.

Ситуация, когда полную группу составляют равновозможные события, называется классической. Поэтому определение вероятности, опирающееся на такое условие называется классическим определение вероятности.

Пусть пространство элементарных событий можно отождествить с мно­жеством G точек, образующих одну из следующих геометрических фигур, — отрезок прямой или дуга кривой конечной длины, ограниченное множество на плоскости или часть поверхности конечной площади, ограниченное мно­жество в пространстве, имеющее объём, — причем по условиям опыта вероят­ность попадания в какую-либо часть множества G пропорциональна мере (длине, площади, объему) этой части и не зависит от ее расположения в G и формы. Тогда вероятность Р(А) события AcG определяется по формуле

Р(А)= мера А /мера G (геометрическая вероятность).

Независимые события. Вероятность произведения двух независимых событий. Вероятность появления хотя бы одного из нескольких независимых в совокупности событий. Условная вероятность. Вероятность произведения двух зависимых событий. Формула полной вероятности. Формула Байеса. Схема Бернулли и формула Бернулли:

Событие В называется независимым от события А, если наступление события А не влияет на появление или непоявление события В. В противном случае события А и В называются зависимыми.

События называются равновозможными, если есть основание считать, что ни одно из них не является более возможным, чем остальные.

Говорят, что несколько случайных событий А₁,…, A_n образуют полную группу событий, если в результате испытания обязательно наступает хотя бы одно из них.

Говорят, что события А₁,…, A_n образуют полную группу равновозможных попарно несовместных событий, если в данном испытании события А₁,…, A_n являются равновозможными и любые два из них – несовместные. Такие события будем называть элементарными событиями (или случаями, исходами).

Элементарное событиеА₁ называется благоприятствующим для появления событии А, если наступление события А₁ влечет за собой появление события А.

Событие, обозначаемое , называется противоположным событием по отношению к событию А, если появление одного из них в результате данного испытания исключает появление другого.

Если Р(А)>0,то Условной вероятностью называется вероятность события В при условии, что событие А уже наступило называется число Р(В/А)=Р(АВ)/Р(А)

Событие В называется независимым от события А, если наступление события А не влияет на появление или непоявление события В. В противном случае события А и В называются зависимыми.

Теорема (вероятность произведения двух независимых событий). Вероятность совместного наступления двух независимых событий равна произведению вероятностей этих событий: Р(АВ)=Р(А)Р(В).

Теорема (вероятность произведения двух зависимых событий). Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие наступило: Р(АВ)=Р(А)Р_А(В) либо Р(АВ)=Р(В)Р_В(А).

Доказательство: n – число исходов, m,k – благоприятствующие события А,В.

Теорема (формула полной вероятности). Вероятность события А, которое может наступить лишь при условии наступления одного из попарно несовместных событий Н1,Н2,…,Нn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Появление события А изменит вероятности 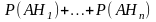элементарных событий. Причем вероятность осуществления события 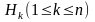после наступления события А определяется следующей формулой Бейеса:

Под схемой Бернулли понимают конечную серию повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают , а непоявления (неудачи) его . Я. Бернулли установил, что вероятность ровно успехов в серии из повторных независимых испытаний вычисляется по следующей формуле:

То значение , при котором число является максимальным из множества { }, называется наивероятнейшим, и оно удовлетворяет условию

np - q m np+ p,

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из событий с вероятностью ( . Вероятность появления раз первого события и - второго и -го находится по формуле

При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

• Случайная величина. Дискретные и непрерывные случайные величины. Закон распределения. Функция распределения случайной величины и ее свойства. Плотность распределения случайной величины, ее свойства:

Случайной называется величина, принимающая в результате испытания только одно значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Различают два типа случайных величин: дискретные и непрерывные.

Случайная величина Х называется дискретной, если в результате испытания она принимает одно из конечного или бесконечного множества значений х₁,х₂,….

Случайная величина Х называется непрерывной, если множество ее значений заполняет полностью некоторый промежуток (a;b).

Законом распределения вероятностей дискретной случайной величины называется зависимость между возможными значениями x_k (k=1,2,…) дискретной случайной величины и их вероятностями p_k (k=1,2,…).

Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, когда в прямоугольной системе координат строят ломанную, соединяющую последовательно точки координатами (x_k; p_k), k=1,2,…. Полученную линию называются многоугольником распределения.
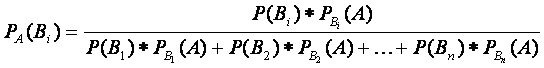