Теория Вероятностей

• Случайные события: Подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом Ω. Пример: Случайный эксперимент состоит в бросании игральной кости: пример случайного события — выпавшее число чётно; события «Выпала единица», «Выпала двойка» и т. д. — элементарные исходы эксперимента; совокупность всех событий «Выпала 1»..«Выпала 6» — полная группа событий.

• Достоверные, невозможные, совместные, несовместные случайные события. Достоверным событием в теории вероятностей называется событие U, которое в результате опыта или наблюдения непременно должно произойти. Обозначается символом Ω. Для достоверного события P(U) = 1.То есть вероятность события U равна единице. Но, не всякое событие, вероятность которого равна 1, является достоверным (см. невозможное событие).Если оговорена некоторая допустимая погрешность (например, 10 ^{− 50}), то событие, вероятность которого не более чем на значение погрешности отличается от 1, называется практически достоверным. Невозмо́жным собы́тием в теории вероятностей называется событие, которое не может произойти в результате эксперимента. То есть событие, не содержащее ни одного элементарного исхода (что соответствует «пустому множеству» Ø в пространстве элементарных исходов). Легко доказать, что вероятность невозможного события равна нулю.Важно заметить, что обратное неверно, то есть из нулевого значения вероятности не следует, того, что данное событие является невозможным. Пример 1: Событие, состоящее в том, что нормальнораспределенная случайная величина примет некоторое конкретное значение. Для любой непрерывной случайной величины верно утверждение: вероятность того, что случайная величина примет определенное, наперед заданое значение равна нулю (P{ξ = x₀} = 0). Пример 2: Эксперимент состоит в том, что монета подбрасывается бесконечное число раз. Событие «Монета бесконечное число раз упадет цифрой вверх» имеет нулевую вероятность, но оно может произойти. При применении вероятностных методов так же вводят определение практически невозможного события. Практически невозможным событием называют событие, вероятность которого не выше определёной наперёд заданной величины. Событие, противоположное невозможному, называется достоверным событием.В теории вероятности – любое событие, которое представляет собой одновременное возникновение любых двух (или более) других событий. При раскладывани и колоды карт, например, "черная пятерка" будет совместным событием, так как состоит из всех карт, которые являются и черными и имеют пять символов. В теории вероятностей несколько событий называются несовместимыми, если никакие два из них не могут появиться одновременно в результате однократного испытания случайного эксперимента. Определение: Если  — вероятностное пространство, и 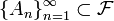 — группа событий, то эти события называются несовместимыми, если они попарно не пересекаются, то есть .

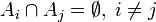• Полная группа событий: В теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1. Определение: Пусть есть вероятностное пространство. Любое разбиение множества Ω элементами сигма-алгебры 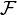называется полной группой событий. Пример: Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий: A: монета упадет орлом;B: монета упадет решкой; C: монета упадет на ребро; Таким образом, система {A,B,C} является полной группой событий.

• Алгебра событий:

Суммой (или объединением) событий А и В называется событие, обозначаемое А+В, которое состоит в наступлении хотя бы одного из событий А или В.

Произведение (или совмещением) событий А и В называется такое событие, обозначаемое АВ, состоящее в одновременном наступлении и события А, и события В.

Если события А₁,…,А_n образуют полную группу попарно несовместных событий, то справедливы равенства: .

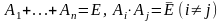Для событий А и 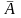справедливы равенства: А+ =Е, 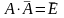Следовательно, событий А и всегда образуют полную группу несовместных событий.

• Аксиомы ТВ:

Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,

   Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B)    Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом.    Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию .    Аксиома 2. Вероятность достоверного события равна единице.    Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:

P(A+B)=P(A)+P(B)

(1)

   Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то

(2)

   Событием, противоположным событию , называется событие , состоящее в ненаступлении события . Очевидно, события и несовместны.    Пусть, например, событие состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие заключается в том, что изделие стандарту не удовлетворяет. Пусть событие — выпадение четного числа очков при однократном бросании игральной кости; тогда — выпадение нечетного числа очков.    Теорема 1. Для любого события вероятность противоположного события выражается равенством

(3)

  Доказательство. Событие + , состоящее в наступлении или события , или события , очевидно, является достоверным. Поэтому на основании аксиомы 2 имеем Р( + )=1. Так как события и несовместны, то используя аксиому 3, получим Р( + )=Р( )+P( ). Следовательно, Р( )+P( )=1, откуда .    Теорема 2. Вероятность невозможного события равна нулю.    Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.