Функция распределения случайной величины, ее свойства.

Функцией распределения (или интегральной функцией распределения) случайной величины Х называется функция F(x), равная при каждом вероятности того, что Х в результате испытания примет значение, меньшее х: F(x)=P(X<x), .

Свойства:

1)

2) F(x) – неубывающая функция.

3) F(x) – непрерывны слева ;

4) ;

5) вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна 0;

6) если Х – непрерывная случайная величина, то функция F(x) непрерывна на .

Плотностью распределения вероятностей (или дифференциальной функцией распределения) непрерывной случайной величины Х называется функция f(x), задаваемая равенством f(x)=F’(x), .

График функции f(x) называется кривой распределения величины Х.

Свойства:

1) ;

2) ;

3) Теорема о вероятности попадания в заданный интервал.

Х – непрерывная случайная величина, f(x) – плотность распределения,

4) условие нормировки;

5) геометрически вероятность попадания случайной величины Х в промежуток (a;b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми x=a, x=b.

6) Если все значения случайной величины Х заключены в промежутке (a₁;a₂), то

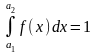
• Функция от случайных величин. Примеры. Математическое ожидание случайной величины. Центрированная случайная величина. Смысл и свойства математического ожидания:

Рассмотрим функцию F(х), определенную на всей числовой оси следующим образом: для каждого х значение F(х) равно вероятности того, что дискретная случайная величина   примет значение, меньшее х, т. е.

(18)

   Эта функция называется функцией распределения вероятностей, или кратко, функцией распределения. 

  Зная функцию распределения F(x), легко найти вероятность того, что случайная величина   удовлетворяет неравенствам  .     Рассмотрим событие, заключающееся в том, что случайняя величина примет значение, меньшее  . Это событие распадается на сумму двух несовместных событий: 1) случайная величина   принимает значения, меньшие  , т.е.  ; 2) случайная величина  принимает значения, удовлетворяющие неравенствам  . Используя аксиому сложения, получаем

   Отсюда

   Но по определению функции распределения F(x) [см. формулу (18)], имеем  ,  ; cледовательно,

(19)

   Таким образом, вероятность попадания дискретной случайной величины в интервал   равна приращению функции распределения на этом интервале.     Рассмотрим основные свойства функции распределения.     1°. Функция распределения является неубывающей.     В самом деле, пусть  < . Так как вероятность любого события неотрицательна, то  . Поэтому из формулы (19) следует, что  , т.е.  .     2°. Значения функции распределения удовлетворяют неравенствам  .     Это свойство вытекает из того, что F(x) определяется как вероятность [см. формулу (18)]. Ясно, что *   и  .     3°. Вероятность того, что дискретная случайная величина   примет одно из возможных значений xi, равна скачку функции распределения в точке xi.     Действительно, пусть xi - значение, принимаемое дискретной случайной величиной, и  . Полагая в формуле (19)  ,  , получим

(20)

   В пределе при   вместо вероятности попадания случайной величины на интервал   получим вероятность того, что величина   примет данное значение xi:

   C другой стороны, получаем  , т.е. предел функции F(x) справа, так как  . Следовательно, в пределе формула (20) примет вид

(21)

   т.е. значение p(xi) равно скачку функции ** xi

Пусть имеется случайная величина Х с математическим ожиданием mx.

Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания. Центрирование случайной величины равносильно переносу начала координат в точку, абсцисса которой равна математическому ожиданию.

Мат ожид приближенно = среднему знач случ величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Если дискретная случайная величина X принимает счетное множество возможных значений, то математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называют определенный интеграл

Если возможные значения принадлежат всей оси Ох, то

M(X)=интегр от – беск до +беск xf (x)dx.

Предполагается, что несобственный интеграл сходится абсолютноСвойства математического ожидания.

1. Математическое ожидание постоянной величины равно самой постоянной.

М(С) = С.

2. Постоянный множитель можно выносить за знак математического ожидания. М(СХ)=СМ(Х).

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

X xi x₂ Y yi у₂

Р Pi Рг g gi g₂

Составим все значения, которые может принимать случайная величина XY

XY xiy, х,у₂ x₂yi х₂у₂

^Р Plgl Plg2 P2gl P2g2

Математическое ожидание равно сумме произведений всех возможных

значений на их вероятности:

Мат ожид суммы двух случ величин = сумме мат ожид слагаемых. М(Х+Y)=М(Х)+М(Y)

• Дисперсия случайной величины, се смысл. Среднеквадратическое отклонение. Свойства дисперсии. Моменты случайной величины:

Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайно величины Х от ее математического ожидания: D(X)=M(X-M(X))².

Свойства: 1) D[C]=0, где C=const.дисп пост вел С =0

2) D[CX]= -постоянный множитель можно выносить за знак дисперсии,возведя его в квадрат

3) X,Y независимы, D[X+(-)Y]=D[X]+D[Y]

4) D[X+C]=D[X]

Для оценки рассеяния возможных значений случ вел вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики.к их числу относят и среднекв отклон.

Среднеквадратическим отклонение случайной величины Х называется число, вычисляемое по формуле

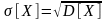
Легко показать,что дисперсия имеет размерность ,равную квадрату размерности случ аеличины.Т.к. среднекв отклон = квадратному корню из дисперсии,то размерность сигма(Х) совпадает с размерностью Х.Поэтому в тех случаях,когда желательно,чтобы оценка рассеяния имела размерность случ велич,вычисляют среднекв отклон,а не дисперсию.

Моме́нт случа́йной величины́ — числовая характеристика распределения данной случайной величины

Если дана случайная величина определённая на некотором вероятностном пространстве, то:

• -м нача́льным моментом случайной величины где называется величина

если математическое ожидание в правой части этого равенства определено;

• -м центра́льным моментом случайной величины называется величина

если математическое ожидание в правой части этого равенства определено. Если определены моменты -го порядка, то определены и все моменты низших порядков В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:

• Биномиальное распределение. Распределение Пуассона и предельная теорема Пуассона. Равномерное и показательное распределение. Математическое ожидание, дисперсия этих распределений:

Биномиальным называется закон распределения дискретной случайной величины X – числа появлений события A в n независимых испытаниях, в каждом из которых появляется либо событие А, либо событие , и вероятность появления события А равна p, а вероятность появления события равна q=1-p.

Тогда P(X=k) – вероятность появления события А ровно k раз в n испытаниях – вычисляется по формуле Бернулли:

Если число испытаний n очень велико, а вероятность p появления события А в каждом испытании очень мала, то для вычисления P(X=k) используют формулу Пуассона: , где . При этом говорят, что случайная величина Ч распределена по закону Пуассона.

Мат ожид этого распредМ=np,а дисперсия D=npq

Распределение Пуассона.

Если число испытаний n очень велико, а вероятность p появления события А в каждом испытании очень мала, то для вычисления P(X=k) используют формулу Пуассона: , где . При этом говорят, что случайная величина Ч распределена по закону Пуассона. Мат ожид и дисперсия = лямбда

Теорема Пуассона в теории вероятностей описывает способ получения распределения Пуассона как предел биномиальных распределений.Формулировка

Пусть есть Пусть также дана последовательность такая, что

Тогда

Равномерное распределение, его числовые характеристики.

Равномерным распределением называется распределение таких непрерывных случайных величин, все значения которых лежат на некотором интервале (a;b) и плотность распределения вероятностей задается формулой: . - функция распределения вероятностей таких случайных величин.

Числовые характеристики непрерывной случайной величины Х, равномерно распределенной в интервале (a;b), вычисляется по формулам: .

Вероятность попадания величины Ч в промежуток (а₁;а₂), где (а₁;а₂) (a;b), вычисляется по формуле: .

Показательное распределение, его числовые характеристики.

Показательным (или экспоненциальным) называется распределение таких непрерывных случайных величин, у которых функция плотности распределения вероятностей задается формулой: , где – некоторое постоянное положительное число.

Функция распределения F(x) таких случайных величин задается формулой:

Для непрерывной случайной величины Х, имеющей показательное распределение вероятностей, числовые характеристики вычисляются по формулам: M(X)=1/λ, D(X)=1/ λ², σ(Х)=1/ λ.

Вероятность попадания величины Х в интервал (a;b) вычисляется по формуле: P(a<X<b)=e^-λa-e^-λb.

• Нормальное распределение. Смысл параметров нормального распределения. Влияние параметров на форму кривой распределения Вероятность попадания значения нормально распределенной случайной величины в заданный интервал. Правило 3-х сигм:

Нормальным называется распределение вероятностей тех непрерывных случайных величин, у которых плотность распределения задается формулой: где – некоторые числа(параметры) Достаточно знать эти параметры, чтобы задать нормальное распределение. Выясним смысл этих параметров и докажем, что m - это математическое ожидание, а сигма -среднеквадратическое отклонение. В зависимости от параметров аист нормальное распределение может называться немного по-разному. Общим называется нормальное распределение с произвольными параметрами м и сигма (сигма>0)

Нормированным называют нормальное распределение с параметрами m=0 и сигма=1. Например, если Х-нормальная величина с параметрами m и сигма, то U=(Х-m)/сигма - нормированная нормальная величина, причем, M(U)=0 и сигма(U)=1. Плотность нормированного распределения задается функцией, которая табулирована. Причем, если F(x) - функция общего нормального распределения, a F₀(x) -

функция нормированного распределения, то легко проверить, что F(x)=Fo((x-m)/сигма).

График плотности нормального распределения называют нормальной кривой или кривой Гаусса. Если исследовать эту функцию, видно, что

Изменение величины параметра m не изменяет форму нормальной кривой, а приводит лишь к ее сдвигу вдоль оси ОХ: вправо, если m возрастает и влево, если m убывает.

По иному обстоит дело, если изменяется параметр сигма. Как уже было выяснено, максимум функции плотности нормального распределения равен 1/[сигма(2пи)^1/2]. Поэтому, с возрастанием сигмы максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси ОХ, при убывании сигмы нормальная кривая становится более «островершинной». Важно отметить, что при любых значениях параметров аист, площадь, ограниченная нормальной кривой и осью ОХ остается равной единице (свойство плотности распределения). При m=0 и сигма=1 кривую называют нормированной.

В случае нормального закона распределения функция распределения вероятностей вычисляется по формуле: , где – функция Лапласа (или интеграл вероятностей, или функция ошибок).

Числовые характеристики случайной величины Х, заданной нормальным законом распределения, вычисляются по формулам: .

Вероятность того, что случайная величина Х примет значения из интервала (a;b), вычисляется по формуле: .

Следствие1: вероятность того, что модуль разности |X-a| меньше некоторого числа δ .

Следствие2: (правило трех сигм): если в следствии1 вместо δ подставить число 3δ, то вероятность того, что модуль разности |X-a|<3δ. На практике правило 3 сигм применяют так:если распределение изучаемой случ вел неизвестно,но условие,указанное в приведенном правиле,выполняется,то есть основание предполагать ,что изучаемая величина распределена нормально.

• Неравенство Чебышева. Закон больших чисел. Предельная теорема Муавра- Лапласа.

Теорема (неравенство Чебышева). Если случайная величина Х имеет конечные математическое ожидание Ь(Х) и дисперсию D(X), то при любом сколь угодно малом ε>0 справедливо неравенство.

Теорема Чебышева. При достаточно большом числе n независимых испытаний среднее арифметическое наблюдаемых значений случайной величины Х сходится по вероятности к ее математическому ожиданию М(Х), то есть где ε – достаточно малое положительное число, δ – зависит от ε и удовлетворяет неравенству: , где D(X) – дисперсия Х.

интегральная теорема Муавра-Лапласа

Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1 ,то вероятность того,что событие А появится в n испытаниях от К1 до К2 раз,приближенно = определенному интегралу:

,

 Математическая статистика

• Основные задачи математической статистики. Генеральная и выборочные совокупности. Выборка. Вариационный и статистический ряды. Гистограмма частот. Эмпирическая функция распределения. Точечные и интервальные оценки. Несмещенная, эффективная, состоятельная оценка.

Математическая статистика разрабатывает методы планирования и анализа эксперимента.

К типичным задачам математической статистики относятся:

- задача определения закона распределения случайной величины по статистическим данным;

- задача нахождения неизвестных параметров распределения случайной величины;

- задача проверки правдоподобия выдвигаемых по статистическим данным гипотез о законе распределения случайной величины, о ее параметрах.

Выборочной совокупностью (или выборкой) называется совокупность случайно отобранных объектов.

Генеральной совокупностью называется совокупность всех однородных объектов, из которых производиться выборка.

Объемом совокупности (генеральной или выборочной) называется число объектов этой совокупности.

Выборка называется представительной (или репрезентативной), если она осуществлена случайным образом, когда все объекты генеральной совокупности имели равные вероятности попасть в выборку.

Вариационным рядом выборки (1.1) называется способ ее запи­си, при котором элементы Xi упорядочиваются по величине, то есть записываются в виде последовательности в порядке их возрастания (верхний индекс), а не в порядке измерений (нижний индекс).

х⁽¹⁾, х⁽²⁾, ... ,х⁽ⁿ⁾, причем х⁽¹⁾ <= х⁽²⁾ < ... < х⁽ⁿ⁾. Каждое значение хi; вариационного ряда называется вариантой.

Разность между максимальным и минимальным элементами вы­борки х⁽ⁿ⁾- х ⁽¹⁾=w называется размахом выборки.

Пусть в выборке объемом n элемент хi встречается ni раз. Число ni называется частотой элемента xi . Очевидно, что

Статистическим рядом называется последовательность пар (xi,ni), которая записывается в виде табл. 1.Таблица 1( Статистическим рядом, соответствующим полученной случайной выборке, называется набор значений (вариант) качественного или количественного признака объектов выборки, которые располагаются в порядке возрастания. )

Xi	X1	х2	..	хк
ni	n1	n2	..	Nк

Отношение wi= ni/ n называется относительной частотой, или ча­стностью элемента хi, выборки. Статистическим распределением случайной величины X называется последовательность пар (хi ,wi), которая также записывается в виде табл. 2.

Таблица 2

Xi	X1	Х2		Xk
wi	w1	w2	…	wk

Заметим, что

Гистограммой ча­стот называют ступен­чатую фигуру, состоя­щую из прямоугольни­ков, основаниями кото­рых служат частичные интервалы длиною h, а высоты равны отноше­нию пi/h (плотность ча­стоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии пi/h. Площадь i-го частичного прямоугольника равна hпi/h=пi—сумме частот вариант i-го интервала; следо­вательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.

На рис. изображена гистограмма частот распреде­ления объема n = 100

Эмпирической функцией распределения случайной величины X называется функция F* (х), определяющая для каждого значения х относительную частоту события (Х< х), т. е. функция вида F* (x)=m/n, ( 1.3 )

где m - число выборочных значений меньших х(хi<х),ап - объем выборки.

Свойства F*(x) аналогичны свойствам теоретической функции распределения F(x) и вытекают непосредственно из определения (1.3), т. е.:

1) значения эмпирической функции распределения заключены между 0 и 1

О < F*(x) <1 ;

2. 

   F *(х) есть неубывающая функция аргумента х ;

3. F *(х)=0 при х< =хi (х i - наименьшая варианта) ; F *(х)=1 при х> х _k (x _k - наибольшая варианта).

Точечные статистические оценки параметров распределения.

Пусть собранный и обработанный статистический материал представлен в виде статистического ряда. Точечной оценкой наз оценку кот определяется одним числом. при выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, те приводить к грубым ошибкам.

Точечной статистической оценкой параметра а распределения случайной величины называется приближенной значений а* этого параметра, вычисленное по статистическим данным.

Любая точечная статистическая оценка некоторого параметра, вычисляемая на основе статистического ряда, должна удовлетворять трем требованиям:

1. при увеличении числа испытаний она должна находиться по вероятности к оцениваемому параметру (свойство состоятельности);

2. математическое ожидание статистической оценки (как случайной величины при изменении числа испытаний) равно оцениваемому параметру (свойство несмещенности);

3. при заданном объеме выборки статистическая оценка имеет наименьшую дисперсию (свойство эффективности)

Интервальной наз оценку, кот определяется двумя числами Qj * и Q₂* – концами интервала, при этом Q попадает в интервал Q1*< Q < Q₂*. Интервальные оценки позволяют установить точность и надежность оценок.

Качество оценок характеризуется некоторыми свойствами. Сфор­мулируем основные из них.

Свойство 1.

Оценка Q* называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть, если M(Q*)=Q. Замечание: Несмещенная оценка является точной в среднем, то есть не­смещенность оценки гарантирует отсутствие систематической ошибки.

Свойство 2.

Оценка Q*(n)=U(xi,x₂,...,x_n) величины Q называется состоя­тельной, если при п —> она сходится по вероятности к Q, то есть при любом е>0 limP(|Q*(n)-Q|<_E)=l.

n—»

Замечание:Состоятельность оценки гарантирует при п ->оо сколь угод­но большую точность оценки с вероятностью, сколь угодно близкой к единице.

Свойство 3.

Несмещенная оценка Q*=U(xi,x₂,...,x_n) величины Q называет­ся эффективной,если ее дисперсия минимальна по сравнению с дис­персиями других несмещенных оценок величины Q при любом, но од­ном и том же п, то есть D(Q*)=M[(Q*-Q)²]=min.

Замечание:Эффективность оценки гарантирует минимум средней квадратической ошибки M[(Q*-Q)²].

• Оценки математического ожидания и дисперсии. Выборочное среднее как несмещенная, состоятельная оценка математического ожидания. Выборочная и исправленная выборочная дисперсия:

В качестве статистической оценки математического ожидания принимают выборочное среднее. В качестве статистической оценки дисперсии D(X) случайной величины X примем выборочную дисперсию.

Выборочным среднем называется среднее арифметическое элементов выборки

(1.4)

Покажем, что выборочное среднее является несмещенной и состоятельной оценкой. Для этого предварительно заметим, что в теоретических рассуждениях выборку x1, x2, ... , х_n обычно рассмат­ривают как некоторую реализацию случайного вектора с n независи­мыми компонентами X1, Х2, ... , х_n , каждая из которых имеет распре­деление генеральной совокупности с теми же числовыми характери­стиками.

С учетом этого замечания установим несмещенность .

M( )=M((l/n) )=M((l/n) )=(l/n)*n*M(X)=M(X).

Состоятельность выборочной средней х как оценки М(Х) следует из закона больших чисел (теорема_Чебышева )[2, 3, 7].

По поводу эффективности заметим, что если случайная вели­чина X распределена по нормальному закону, то выборочное среднее является эффективной оценкой математического ожидания.

Выборочной дисперсией называется среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выбороч­ного среднего

S² = (l/n) (_Xi- )². (1.5)Можно показать, что оценка S² является смещенной. Для полу­чения несмещенной оценки дисперсии выборочную дисперсию S исправляют, умножая ее на множитель n/(n-1). Исправленная дис­персия

So² =(n/(n-l))S²=(l/(n-l)) (_Xi -x)² (1.6 )является уже несмещенной оценкой дисперсии. Оценка S² (а вместе с ней и S₀²) состоятельна.

• Точность и надежность оценки. Доверительный интервал. Доверительные интервалы для оценки математического ожидания и срсднсквадратичсского отклонения нормального распределения.

Для выборок небольшого объема вопрос точности оценок решается с помощью интервальных оценок. При этом по вычисленной точечной оценке а* параметра а при заданной вероятности γ и а*, строят интервал для истинного параметра а: а*- ε<a<а*+ ε, чтобы выполнялось равенство: P(а*- ε<a<а*+ ε)=γ. Число ε называется точностью оценки а*, границы интервала а*- ε и а*+ ε называются доверительными границами, интервал (а*- ε;а*+ ε) – доверительным интервалом, вероятность γ – доверительной вероятностью или надежностью интервальной оценки.

Интервальной оценкой математического ожидания m нормального распределения при известной дисперсии σ² называется интервал , удовлетворяющий равенству: , где – заданная доверительная вероятность, m – истинное математического ожидание, – точечная оценка математического ожидания, n – объем выборки; число находится из уравнения с помощью табл.2 функции Лапласа Ф(х).

Следовательно, интервальная оценка математического ожидания находится по формуле:

Интервальной оценкой математического ожидания m нормального распределения при неизвестной дисперсии называется интервал , удовлетворяющий равенству: где – заданная доверительная вероятность, m – истинное математическое ожидание, – точечная оценка математического ожидания, s² – точечная оценка дисперсии, n – объем выборки, число вычисляется из уравнения с помощью таблицы распределения Стьюдента. Следовательно, интервальная оценка математического ожидания с доверительной вероятностью вычисляется по формуле: .

Интервальной оценкой среднего квадратического отклонения σ нормального распределения называется интервал: удовлетворяющий равенству где – заданная доверительная вероятность, s² – исправленная выборочная дисперсия, n – объем выборки, число определяется ил таблицы4.

Следовательно, интервальная оценка среднего квадратического отклонения находится по формулам: если , если .

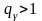• Статистическая проверка гипотез. Виды гипотез. Ошибки первого и второго рода. Статистические критерии проверки нулевой гипотезы. Критическая область. Проверка гипотез для нормального распределения

Статистической гипотезой называется предположение о виде распределения, о параметрах известных распределений. Например, стат.являются гипотезы: 1) генеральная сов-ть распределена по закону Пуассона( здесь сделано предложение о виде неизвестного распределения); 2) дисперсия двух нормальных сов-тей равны между собой (о параметрах двух известных гипотез)

Выдвинутая гипотеза называется нулевой (или основной) и обозначается Н_о.

Гипотеза, которая противоречит нулевой, называется конкурирующей гипотезой (или альтернативной гипотезой) и обозначается Н₁.

Гипотеза называется простой, если она содержит только одно предположение.

Гипотеза называется сложной, если она состоит из конечного или бесконечного числа предположений.

Ошибкой первого рода называется решение отвергнуть нулевую гипотезу H_o и принять конкурирующую гипотезу Н₁, если на самом деле гипотеза Н_о верна. Вероятность ошибки первого рода равна уровню значимости α.

Ошибкой второго рода называется решение принять нулевую гипотезу Н_о, то есть отвергнуть конкурирующую гипотезу Н₁, если на самом деле гипотеза Н₁ верна.

Гипотеза Н₀ проверяется с помощью статистического критерия.

Статистическим критерием (критерием) называют однознач­но определенное правило, устанавливающее условия, при которых проверяемую гипотезу Но следует или отвергнуть, или принять. В ос­нове критерия- функция Т= Т( х1, ..., хn) от выборочных данных (т. е. статистика критерия ), распределение которой известно. Примера­ми таких распределений, на основе которых построено большинство критериев, являются: нормальное, х2(хи-квадрат) - распределение, распределения Стьюдента и Фишера.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотез (об допустимых значений) называют совокупность значений критерия, при кот гипотезу принимают. Критическими называются точки, отделяющие критические области от областей принятия гипотез.

Различают правостороннюю, левостороннюю, двустороннюю критические области Правосторонней критической областью для проверки нулевой гипотезы с уровнем значимости α называется совокупность значений критерия проверки Z, для которых выполняется равенство: P(Z>Z_крит)= α. При этом Z_крит называется границей критической области.

.

Правосторонняя критическая область определяется неравенством: Z> Z_крит.

Левосторонняя критическая область определяется неравенством: Z<- Z_крит.

Односторонней называют правостороннюю или левостороннюю критическую облась.

Двусторонняя критическая область определяется неравенствами Z> Z_1крит и Z> Z_2крит.