14. Определение и примеры векторного пространства, векторов, линейной комбинации векторов.

Векторное пространство-непустое множество, в котором определенны две операции(сложение и умножение на число), относительно которых выполнены все аксиомы линейных операций над любыми n-мерными векторами. Например: n-мерные векторы образуют векторное пространство, которое обозначается как Rⁿ. Вектор в линейной алгебре — элемент векторного пространства. Линейная комбинация векторов — вектор, представленный в виде x = α_ia_i +... + α_na_n, где коэффициенты α_i — произвольные числа; a_i — рассматриваемые векторы (i = 1, ..., n).

15. Определение линейной зависимости и независимости системы векторов. Формулировка основных свойств линейно независимых векторов.

Векторы а1,а2,…аn пространства Rⁿ называются линейно независимыми, если уравнение α₁a₁+α₂a₂+…+α_na_n=0 имеет единственное нулевое решение α₁=0,α₂=0,α_n=0.

Векторы а₁,а₂,…а_n пространства Rⁿ называются линейно зависимыми, если найдутся числа α₁,α₂,α_n, неравные нулю, для которых выполнено равенство α₁a₁+α₂a₂+…+α_na_n=0. Свойства: линейно зависимо

M линейно независимо   M' линейно независимо для всех 

M линейно зависимо   M' линейно зависимо для всех 

16. Определение базиса и размерности векторного пространства.

Базисом векторного пространства называется упорядоченный набор e1,e2,…,en линейно независимых векторов, через которые любой вектор x пространства линейно выражается, т.е. существуют такие α₁,α₂,…,α_n, что x=α₁e₁+α₂e₂+…+α_ne_n.

Размерностью векторного пространства называется число векторов в каком-либо базисе. Обозначается dim. (dimR²=2, dimR³=3 и т.д.)

17. Определение матрицы перехода и её свойства.

Матрицей перехода от базиса   к базису   является матрица, столбцы которой - координаты разложения векторов   в базисе  .

С войства: 1.Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю. 2.

18. Три определения ранг матрицы. Формулировка теоремы о ранге матрицы.

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.

Теорема о ранге матрицы: Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).

19. Определения однородной слу, фундаментальной системы решений.

С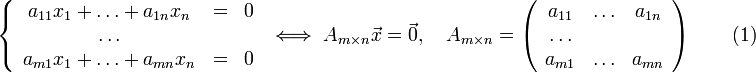 истема линейных уравнений называется однородной, если все входящие в нее уравнения являются линейными однородными уравнениями. СЛОУ – это СЛУ, если свободные члены равны нулю. x1=x2=x3=...=xn=0 – это и есть решение системы. Такая система всегда совместна.

ФСР – это базис пространства решений. Любое решение системы линейно выражается через фундаментальную систему.