1. Решение дифференциального уравнения методом Эйлера.

2. Найти интерполяционный полином 2 степени методом Лагранжа.

3. Провести оптимизацию полученного полинома методом Дихотомии.

4. Найти значения определенного интеграла методом Симпсона.

5. Составить блок-схемы алгоритмов и программы для приведенных решений на языке высокого уровня программирования.

Объект исследования – информатика специальные главы.

Предмет исследования - дифференциальное уравнение.

1.Методы решение дифференциального уравнения

Дифференциальное уравнение-уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.

Наиболее простым численным методом решения дифференциальных уравнений является метод Эйлера, который был описан в 1768 году в работе «Интегральные исчисления». Из-за своей простоты метод Эйлера находит своё применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

y_i=y_i-1+h*f(x_i-1;y_i-1)

где h-шаг.

1.1 Интерполяционные формулы — в математике формулы, дающие приближённое выражение функции   при помощи интерполяции, то есть через интерполяционный многочлен   степени  , значения которого в заданных точках   совпадают со значениями   функции   в этих точках. Многочлен   определяется единственным образом, но в зависимости от задачи его удобно записывать различными по виду формулами. Интерполяционная формула Лагранжа обеспечивает построение алгебраического многочлена P_n(x) для произвольно заданных узлов интерполирования. Для n + 1 различных значений аргумента x₀, x₁, ..., x_n и соответствующих значений функции f(x₀) =  y₀, f(x₁) =  y₁, ..., f(x_n) =  y_n

1.2 Оптимизация полинома методом Дихотомии.

Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у неё есть корень, как минимум один. Именно на базе этой теоремы и построено численное нахождение приближенного значения корня функции. Обобщенно этот метод называется дихотомией т.е. делением отрезка на 2 части. Алгоритм выглядит так:

•Задать начальный интервал.

• Убедиться, что на концах функция имеет знак.

• Повторять.▫

▫Выбрать внутри интервала точку X.

▫Сравнивать знак функции в точке Х со знаком функции в одном из концов.

▫Если совпадает, то переместить этот конец интервала в точку Х.

▫Иначе переместить в точку Х другой конец интервала.

Повторять до тех пор, пока не будет достигнута нужная точность.

1.3 Интегрирование методом Симпсона.

Метод Симпсона, названый в честь британского математика Томаса Симпсона, относится к приемам численного интегрирования, суть которого заключается в приближении подынтегральной функции на отрезке [a,b] интерполяционным полиномом второй степени.

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a,b]

2.Практическая часть.

uses crt;

var xi,y:real; klava:integer;

const h=0.1; //шаг

a=0; //начальное значение отрезка

b=1; //конечное значение отрезка

n=2; //степень полинома

//1

function fak(x,y:real):real;

begin

fak:=2*(sqr(x)+y); //исходное диф. уравнение

end;

function ailer(xi:real):real;

var x,y,r,pt:array[1..20] of real; i,j,k,m:integer;

begin

writeln ('Таблица значений:');

x[1]:=a;

y[1]:=1;

k:=1;

repeat

writeln('x',k,'=',x[k]:0:3,' y',k,'=',y[k]:0:3);

inc(k);

y[k]:=y[k-1]+h*fak(x[k-1],y[k-1]);

x[k]:=x[k-1]+h;

until not (x[k]<b);

end;

//2

function lagrang(xi:real):real;

var x,y,r,pt:array[1..20] of real; ct,u:real; i,j,k,m:integer;

begin

x[1]:=a;

y[1]:=1;

k:=1;

repeat

inc(k);

y[k]:=y[k-1]+h*fak(x[k-1],y[k-1]);

x[k]:=x[k-1]+h;

until not (x[k]<b);

for i:=1 to n+1 do

r[i]:=0;

for i:=1 to n+1 do

begin

ct:=1; pt[1]:=1; k:=1;

for j:=1 to n+1 do

if i<>j then

begin

ct:=ct*(x[i]-x[j]);

pt[k+1]:=1;

if k>1 then

for m:=k downto 2 do

pt[m]:=pt[m-1]-pt[m]*x[j];

pt[1]:=-pt[1]*x[j];

k:=k+1;

end;

u:=y[i]/ct;

for m:=1 to n+1 do

r[m]:=r[m]+pt[m]*u;

end;

writeln(' Интерполяционный полином Лагранжа ',n, ' -ой степени :');

writeln('Q(x)=',r[1]:0:2,'+',r[2]:0:2,'x+',r[3]:0:1,'x^2');

end;

//3

function q(x:real):real;

begin

q:=1+1.79*x+2.1*sqr(x); //полученный полином Лагранжа 2-й степени

end;

function dixotomiya(xi:real):real;

const eps=0.1; // точность метода дихотомии

var

x, a, b,t,d,c,g: real;

k: Integer;

begin

writeln ('Оптимизация полинома');

a:=0; b:=1;

t:=0; d:=1;

repeat

c := (a + b) / 2;

if (q(a) * q(c)) < 0 then b := c

else a := c;

inc(k)

until (b - a) <= eps;

x:= (a + b) / 2;

writeLn('корень(максимум) x=', x:5:5);

repeat

g := (t + d) / 2;

if (q(a) * q(b)) < 0 then d := g

else d := g;

inc(k)

until (d - t) <= eps;

x:= (t +d)/2 ;

writeLn('корень (минимум) x=', x:5:5);

readln;

end;

//4

function integral(xi:real):real;

var h,x:real;

n,i :integer;

integ :real;

begin

write('Введите количество разбиений интервала(четное число) n='); readln(n);

if (n mod 2)>0 then { mod-остаток от деления n на 2 с остатком}

begin

n:=n+1;

writeln('число n было нечетно, она заменено на n=',n);

end;

h:=(b-a)/n;

integ:=q(a)+q(b)+4*q(a+h);

for i:=1 to (n div 2)-1 do {частное деление n на 2 с остатком}

begin

x:=a+2*h*i;

integ:=integ+2*q(x)+4*q(x+h);

end;

integ:=h*integ/3;

writeln('Интеграл равен ',integ:3:3);

end;

begin

writeln ('Введите номер задания:');

writeln('1)Решить диф.уравнения dy/dx=2*(x^2+y),y(0)=1 на отрезке [0;1] методом Эйлера;');

writeln('2)Найти интерполяционный полином Лагранжа 2-ой степени;');

writeln('3)Провести оптимизацию полученного полинома методом дихотомии;');

writeln('4)Найти определенный интеграл методом Симпсона.');

readln(klava);

case klava of

1: writeln(ailer(xi));

2: writeln(lagrang(xi));

3: writeln(dixotomiya(xi));

4: writeln(integral(xi));

end; end.

Рисунок 1-полученные значения

2.Составим Блок-схему алгоритма программы

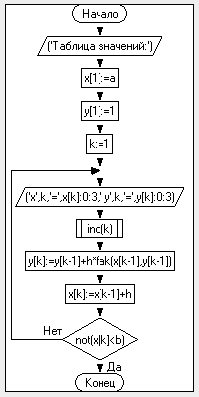
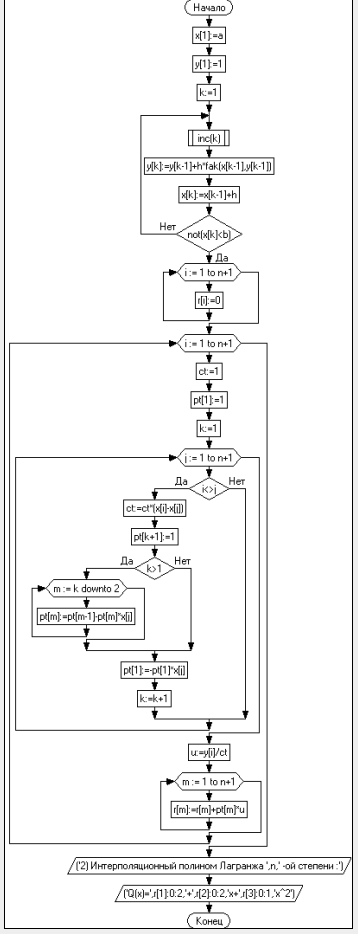
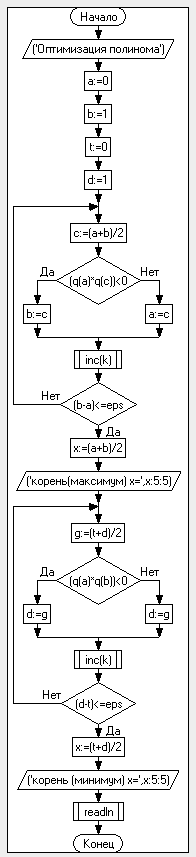
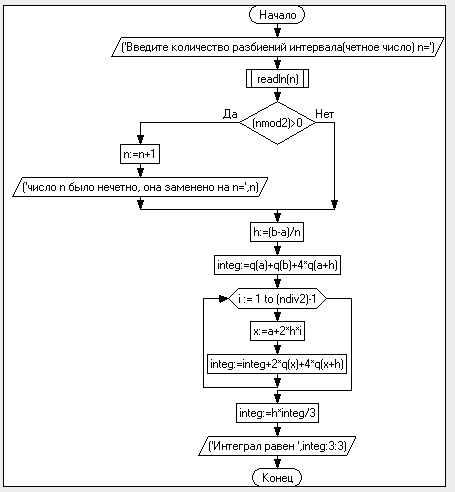
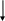
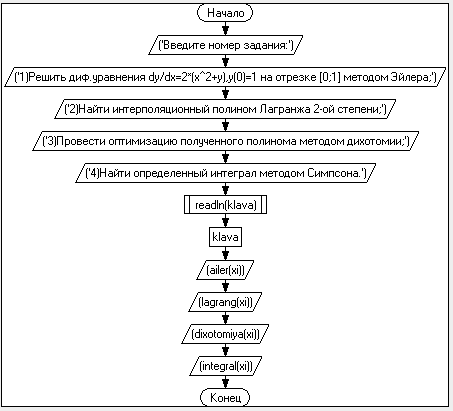
Рисунок 2-Блок-схема алгоритма

Заключение

Освоение методов решения дифференциальных уравнений, в ходе выполнения курсовой работы, позволяет проводить различные вычислительные операции, которые упрощают вычисления.

Метод Эйлера позволяет вычислить дифференциальное уравнение за короткое время. Легок в работе и освоении.

Интерполяция методом Лагранжа проста в освоении, но сложна в вычислении.

Метод дихотомии очень прост в освоение, но из-за повышении точность повышается и число итераций.

Формула Симпсона проста в использовании, и при том условии, что четвертая производная не слишком велика, дает высокую точность.

Данные методы были реализованы на языке высокого уровня программирования PASCAL и показали свою эффективность в вычислениях.

Список литературы:

1. Абрамов В.Г., Трифонова Г.Н. Введение в язык Паскаль. – М.: Наука, 1988.

2. Задачи по программированию / С. А. Абрамов, Г. Г. Гнездилова, Е. Н. Капустина, М. И. Селюн. – М.: Наука, 1988.

3. Могилев А.В., Пак Н.И., Хеннер Е. К. Информатика: учеб. Пособие для студ. пед. Вузов / под ред. Е.К. Хеннера. – М.: Изд. Центр «Академия», 1999.

4. Касаткин В. Н. Информация. Алгоритмы. ЭВМ – М.: Просвещение, 1991.

5. http:// ru.wikipedia.org