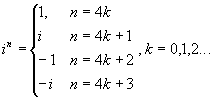
Неравенства треугольника z₁+z₂ z₁+z₂;

z₁-z₂ z₁-z₂

При умножении двух комплексных чисел их модули перемножаются, а аргументы складываются

При делении двух комплексных чисел их модули делятся, а аргументы вычитаются

Возведение в целую степень. zⁿ=[(cos+isin)]ⁿ=[e^i]=

=ⁿe^in=  ⁿ(cos(n)+isin(n));  Формула Муавра:

(cos+isin )ⁿ = cos(n)+isin(n)

Извлечение целого корня

Неограниченно возрастающие последовательности  .Если для  A>0  N: для  n>Nz_n>A, то последовательность {z_n} называется неограниченно возрастающей. Примеры. а) z_n=zⁿ при |z|>1;

б) z_n= i n. В обычном смысле они не сходятся, но оказывается удобным считать, что  z = ;  z_n= . Единственная бесконечно удаленная точка комплексной плоскости. Все неограниченно возрастающие последовательности сходятся к этой единственной точке. Правила арифметических действий с бесконечно удаленной точкой: 1/ =0,. 1/0= , z = , z 0, z+ = , z/ =0, z . Операции 0/0 и  / являются неопределенными.

Точка z₀ называется внутренней точкой мн-ва g, если   -окр. точки z₀ :

z-z₀<все точки котор. g.

Точка z₀ называется граничной точкой множества g, если в  ее -окрестности имеются как z g, так и z g.

Рассмотрим случай, когда w=f(z) задана в g и отображает g на область D комплексной плоскости w. Отображение однозначно. Если z₁, z₂  g и z₁ z₂ : f(z₁)=w₁ w₂= f(z₂), то отображение взаимно однозначно. В этом случае g называется областью однолистности f(z) и f(z) называется однолистной в g.

Функция f(z) C(g), дифференцируемая во всех точках z g, производная которой f ' (z) C(g) называется аналитической функцией в области g.

Если f(z)=u(x,y)+iv(x,y) дифференцируема в точке z₀, то u_x(x₀,y₀), u_y(x₀,y₀), v_x(x₀,y₀), v_y(x₀,y₀), причем они связаны условиями Коши-Римана: u_x(x₀,y₀)=v_y(x₀,y₀) ; u_y(x₀,y₀)=-v_x(x₀,y₀).

Действительная и мнимая части аналитической функции удовлетворяют уравнению Лапласа:

u_xx+u_yy=u=0

v_xx+v_yyv=0

Действительная и мнимая части аналитической функции f(z)=u(,)+iv(,) комплексной перемен. z=e^i

связаны соотношениями:

v_ =u_ , u_ = -v_

Модуль и аргумент аналитической функции f(z)=R(x,y)e^{i (x,y)}

связаны соотношениями:

R_x=R_y,  R_y=-R_x

Необходимым и достаточным условиями аналитичности функции f(z)=u(x,y)+iv(x,y) в области g, являются непрерывность первых частных производных u_x, u_y, v_x, v_y и связь их условиями Коши-Римана.

Св-ва аналитических функц:

1.Если f(z) аналит. в g, то она непрер. в этой области.

2.+ и * аналит.ф-ций – аналит. ф-ция. Частное аналит. Ф-ций – аналит. ф-ция всюду, где знаменатель отличен от нуля.

3.Если w=f(z) – аналит.ф-ция в обл. g, причем в обл. её значений G на плоск. w опред. аналит.ф-ция =(w), то ф-ция F(z)=[f(z)] – аналит.ф-ция компл. переменной z в обл. g.

4. .Если w=f(z) – аналит.ф-ция в обл. g, причем |f ’(z)|≠0 в окр. некот. точки z₀ g, то в окр. точки w₀=f(z₀) обл.G значений ф-ции f(z) определ. обратн. ф-ция z=(w), являющ анал.ф-цией компл.перем. w. Справ. соотн. '(w₀)=1/f '(z₀).

5.Пусть в обл.g задана ф-ция u(x,y), являющ. действ. частью аналит.ф-ции f(z). Тогда мнимая часть этой ф-ции определяется с точностью до аддитивной постоянной.

6. grad u=(u_x,u_y), grad v=(v_x,v_y), (grad u, grad v)=u_xv_x+ u_y v_y= -u_y v_y+ u_y v_y=0. Т.к. градиент ортогонален линии уровня => линии уровня u(x,y)=c, v(x,y)=c взаимно ортогональны.

Необходимым и достаточным условиями аналит. ф-ции f(z)=u(x,y)+iv(x,y) в области g явл. требование, чтобы ф-ции u(x,y) и v(x,y) были гармон. и удовл. усл. Коши-Римана.

Теор. о нулях аналит. ф-ции.

Если нули функции f(z), аналит. в обл. D, имеют предельную точку внутри D, то ф-ция f(z)=0 всюду в D.

След.: если ф-ция f(z) аналит. в обл. D и ≠тождественно 0, то в любой огран.замкн. подобл. у неё может быть лишь конечное число нулей.

Теор.Един.Опр.Аналит.Ф-ции

Пусть {z_n} — сходящ.посл-сть различ. точек обл. D. Если две аналит. ф-ции f(z),g(z) совп. во всех точках этой посл-сти, то они тождеств. равны в D.

Точка z₀ является нулем кратн. k аналит. ф-ции f(z) если f(z₀)=0, f^(k-1)(z₀)=0, f^(k)(z₀)≠0

В ε-окресн. k-того нуля f(z) представима в виде:

f(z)= , a_k≠0,

|z-z₀|<ε

Точка z ₀ g называется правильной точкой ф-ции f(z), заданной в g, если

 c_n(z-z₀)ⁿ =f(z) в g |z-z₀| < (z₀), где (z₀)-радиус сх-сти степ. ряда. Все остальные точки z g- особые точки функции f(z), заданной в g.

Интегр. от ф-ции компл. перемен. f(z)=u(x,y)+iv(x,y) по кривой C компл. пл-сти z называется компл. число, действ. и мнимая части которого – криволин. инт. 2 рода от действ. и мнимой частей f(z) вида: f(z)dz = [u(x,y)+iv(x,y)](dx+idy)= udx-vdy +i vdx+udy.

Свойства f(z)dz

1.

2.

3.

4.Интеграл суммы=сумме интегралов

5.

Интегр.по пар-тру:

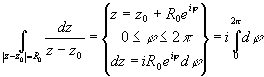
=2 i . Результат не зависит ни от R₀, ни от z₀

Замена переменных. Пусть  (): z=(); C<=>  на плоскости  и  ( ) C (D) и однолистная в D, где D- область комплексной плоскости  , содержащая  . => f(z)dz= f[()]'()d

Теорема Коши. Если f(z) C (g), в односвязн. обл. g, то замкн. контура  g

  f(z)dz =0.

Т-ма Коши для многосв.обл.

Пусть f(z) C (g), g-многосв., огран. извне конт. C₀, а изнутри- конт. C₁, C₂,...,C_n и пусть f(z) C ( ). Тогда f(z)dz =0,  где С-полная граница g, С= C₀ C₁ C₂ ... C_n, проходящая в положительном направлении.

Пусть g-односв. обл., f(z) C(g),  замкн. конт.  g  интеграл 

f(z)dz =0. Фция 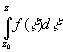 =F(z)- называется неопредел. интегралом от  f(z).

Усл-ия аналит.неопр.инт. Если g-односв. и f(z) C(g) и  замкн. контура  g  интеграл  f(z)dz =0, то F(z)  и F(z) C (g).

Пусть f(z) C(g). Тогда первообр. F(z) ф-ции f(z) в g называется  F(z) C (g) такая, что F '(z)=f(z).

Ф-ла Ньютона-Лейбн. Если g-односв. и и f(z) C(g) и  замкн. контура  g  интеграл  f(z)dz =0, то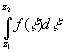 =F(z₂)-F(z₁); где F-  первообразная.

Интегр.ф-ла Коши.

f(z) – аналит. в односв. обл. g, z₀ – внутри замк.конт.Г

Пусть z₀- некоторая внутр. точка односв. обл. g. Возьмем окружность с центром в z₀ и радиусом R, целиком лежащую в g. Тогда f(z₀)= =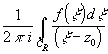

=(= z₀+Re^i)= f(z₀+Re^i)d = f()ds (ds=Rd)- ф-ла ср. значения.

Принцип максимума модуля:

f(z)-аналит. в обл.g,непрер.в замкн.обл.g*.Тогда или |f(z)|≡const или максим.значен. |f(z)| дост-ся то-ко на гран.обл.

Пусть C- кусочно-гладкая кривая конечной длины L:  ds=L и f( ) непрерывна вточке C. Тогда при z C  F(z)=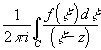 - интеграл типа Коши.

В  z₀ C    F(z₀)- дифф-ма  и F '(z₀)= .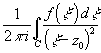

Производн.высш.порядков для аналит.ф-ции

f(z)-аналит.в обл.g и непрер. в замкн.обл.G. Тогда во внутр.точках обл.g Ǝ произв.любого порядка ф-ции f⁽ⁿ⁾(z)=

Т-ма Морера:Если f(z) C(g), g-односв. и для   g:  f(z)dz=0, где  -замкнутый контур, который можно стянуть в точку, оставаясь в g, то f(z) C (g).

Т-ма Лиувилля: Если f(z) C и (|f(z)|- равномерно ограничен), то f(z) const.

f(z) C (E)(на всей компл. пл-сти) (z ) называется целой ф-цией. Целая ф-ция const не может быть огран. по абсолютной величине. Пример: f(z)=zⁿ

Критер.Коши для ЧР: для того чтобы ЧР сх-лся равном.в обл.g необх.и дост. чтобы  ε>0 ƎN такое что  n≥N и m во всех точках обл.g вып-тся:

│S_n+m(z) – S_n(n)│<ε

Необх. признак сх-сти ряда: a_n 0 при n .

Пр. Даламбера: Если начиная с некот. N выполн. нер-во  |a_n+1/a_n| L<1 для n N, то ряд  |a_k| сходится.

Предельная форма: Если  |a_n+1/a_n|=L, то при L<1 ряд  |a_k| сх-ся, при L>1 ряд a_k расх-ся,при L=1 ничего сказать нельзя.

Пр.Коши:Если начиная с нек. N  L<1 для n N, то ряд  |a_k| сходится

Предельная форма: Если  =L, то при L<1 ряд  |a_k| сх-ся,при L>1 ряд a_k   расх-ся,при L=1 ничего сказать нельзя.

Кр.Коши для ФР: >0 N: n N и m>0 |S_n+m(z)-S_n(z)| <

Если >0 N что n N и  z |f(z)- u_k(z)| < ε ряд называется равномерно сх-ся к функции f(z) в g

Кр.Коши равн.сх-сти ФР: Если >0 N такое,чтоn N и m>0 и z:| S_n+m(z)-S_n(z)| <, то ряд . u_k(z)=>f(z).

Пр.Вейерштр.равн.сх-сти: Если |u_k(z)|<a_k, a_k>0 k N и z g и  a_k сходится, то  u_k(z)=>f(z) в g.

Почленное интегр.ФР: Пусть u_k(z) С(g) и  u_k(z)=>f(z). Пусть С кус.- гладкий контур конечной длины L тогда u_k(z)dz= u_k(z)dz

Т-ма Вейерштр.для рядов аналит.ф-ций: Если u_k(z) C (g) и  u_k(z)=>f(z), для z  ' g, (замкн. подобл. обл. g) то:    1.    f(z) C (g).    2.    f^(p)(z)= u_k^(p)(z), для z g.    3.  u_k^(p)(z)=>f^(p)(z), для z  ' g.

2я т-ма Вейерштр.: Пусть u_k(z) C ( ) и  u_k()=>f(), для  g. Тогда  u_k(z)=>f(z), z .

Т-ма Абеля для СР: Если СР  c_n(z-z₀)ⁿ сх-ся в точке z₁ z₀ , то он сх-ся и z:

|z-z₀|<|z₁-z₀|, причем в круге

|z-z₀| <|z₁-z₀| сх-ся равномер

Круг/радиус сх-сти: Рассмотрим sup|z₁-z₀|=R z₁ , где ряд сх-ся- точную верхнюю грань расстояний от точки z₀ до точек z₁ в кот.сх-ся ряд  c_n(z-z₀)ⁿ . Если R тоz₂: |z₂-z₀ |>R ряд расх-ся. inf|z₂-z₀|=R z₂,где ряд расхся. ПустьR>0, тогда наибол. обл. сх-сти СР является |z-z₀|<R - круг сх-сти СР, число R>0- радиус сх-сти СР.

Обл.равн.сх-сти ЧР: В круге |z-z₀| <R СР сх-ся равномерно. По т.Вейерштр. СР внутри круга сх-сти можно диф-вать и интегр.почленно любое число раз. При этом радиус сх-сти не меняется

c_n(z-z₀)ⁿ=f(z)=> c₀=f(z₀), c_n+1(n+1)(z-z₀)ⁿ=

=f '(z)=> c₁=f '(z₀)… c_n+k(n+k)!(z-z₀)ⁿ=f^(k)(z)=> c_k=f^(k)(z₀)/k!

(z-z₀)ⁿ : c_n=1 => R=1. S_n=[1-(z-z₀)ⁿ⁺¹]/[1-(z-z₀)];

|z-z₀|<1 и  S_n=1/[1-(z-z₀)]. =>  (z-z₀)ⁿ=1/[1-(z-z₀)]- Формула суммы бесконечной геометрической прогрессии.

Т-ма Тейлора: Если f(z) C (|z-z₀ |<R), то СР c_n(z-z₀)ⁿ=>f(z) при

|z-z₀|<R.