10. Определение наличия автоколебаний в нелинейной сау

Построим модель исследуемой САУ с нелинейным элементом типа реле с зоной нечувствительности:

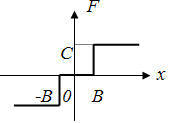
Рис. 17. Нелинейность типа реле с зоной нечувствительности

Для нелинейности типа реле с зоной нечувствительности при :

В соответствии с заданием B=C=1.

Рис.18. Модель нелинейной САУ

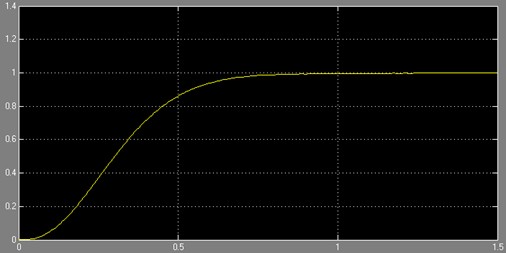
Рис.19.Переходной процесс нелинейной САУ

Из переходной характеристики видно, что система является устойчивой.

Наличие автоколебания определяем по методу Гольдфарба. Для этого в Matlab строим АФХ линейной и нелинейной частей.

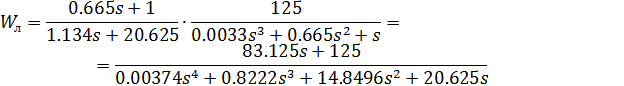
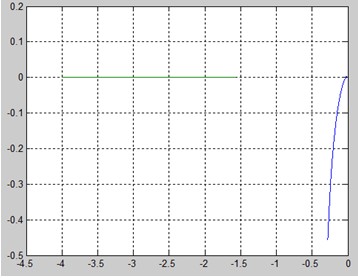
Рис. 20. АФХ линейной и нелинейной частей системы

АФХ линейной и нелинейной не пересекаются, что свидетельствует об отсутствии периодических движений.

11. Анализ абсолютной устойчивости нелинейной системы

Анализировать абсолютную устойчивость будем по методу Попова, для этого построим модифицированный годограф, умножив мнимую часть передаточной функции на ω. Построим модифицированный годограф в Matlab.

k=1; w=0; u=[]; v=[];

while w<=100,s=j*w;

f=(0.0302*s^2+2.62*s+10)/(0.00495*s^4+0.114*s^3+1.1752*s^2+3.1*s)

u(k)=real(f);v(k)=imag(f)*w;

w=w+0.01;k=k+1;

end

plot(u,v);grid

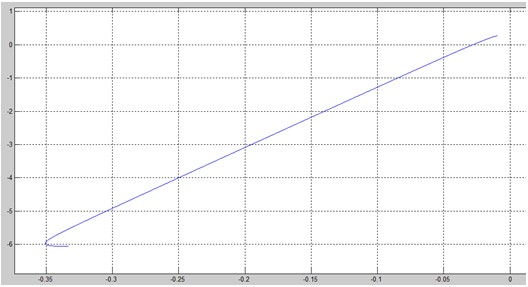
Для нелинейности типа реле с зоной нечувствительности при B=C=1, следовательно k=1.

Система абсолютно устойчива, т.к. через точку -1/K=-1/1=-1 можно провести множество прямых, которые находятся слева от модифицированного годографа.

Заключение

В данной работе было проведено исследование системы углом, в ходе которого были синтезированы корректирующие устройства для достижения требуемых показателей качества. Синтез проводился методом Соколова Н.И.. В результате была получена скорректированная система, полностью удовлетворяющая показателям качества. Также была исследована система с нелинейным элементом типа “ступенька ” на возникновение периодических движений и абсолютную устойчивость. Система с нелинейным элементом устойчива и у нее нет неустойчивых периодических движений.

Список использованной литературы

1. Методические указания к курсовой работе по дисциплине "Теория управления" для студентов специальности 210100 - "Управление и информатика в технических системах" Уфимск. гос. авиац. техн. ун-т; Сост. Б.Г. Ильясов, Л.А. Болотовская. Уфа, 1998.- 24 с.

2. Конспекты лекций и практических занятий.

Размещено на Allbest.ru