Размещено на http://www.allbest.ru/

Введение

В теории автоматического регулирования основными являются проблемы: устойчивости, качества переходных процессов, статической и динамической точности, автоколебаний, оптимизации, синтеза и отождествления .Задачи общей теории автоматического регулирования заключаются в решении перечисленных проблем.

Задача коррекции состоит в повышении динамической точности САР в переходных режимах. Она возникает, поскольку стремление снизить ошибки регулирования в типовых режимах, приводит к необходимости использования таких значений общего коэффициента усиления, при которых без принятия специальных мер (внедрения пассивных звеньев) система оказывается неустойчивой.

Синтез системы имеет конечной целью отыскание:

1) рациональной структуры системы

2) установление оптимальных величин параметров отдельных звеньев.

Задача повышения точности САР обычно предполагает существенный пересмотр ее структуры. Возможны замены или добавления отдельных звеньев в контуре.

1. Определение передаточных функций разомкнутой системы, разомкнутой системы по возмущению, замкнутой системы, замкнутой системы по возмущению, замкнутой системы относительно ошибки по задающему и возмущающему воздействиям

Передаточная функция разомкнутой системы

Передаточная функция разомкнутой системы по возмущению

Передаточная функция замкнутой системы

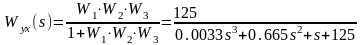
Передаточная функция замкнутой системы по возмущению

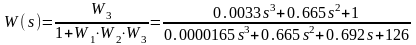
Передаточная функция замкнутой системы относительно ошибки по возмущающему воздействию

Передаточная функция замкнутой системы относительно ошибки по задающему воздействию

2. Построение модели исследуемой сау, используя Matlab (Simulink)

Рис.1 Модель нескорректированной исследуемой САУ

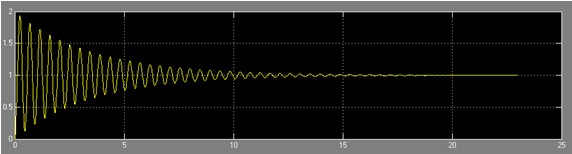
Рис.2. Переходная характеристика нескорректированной исследуемой САУ

Из рисунка 2 видно, что исследуемая САУ устойчива. Определим показатели качества.

,

где - макс. значение переходной характеристики замкнутой САУ

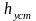, - установившееся значение .

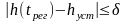
Время регулирования tрег - минимальная величина, при которой удовлетворяется условие: ,где

- заданная величина ошибки (обыч но =0.05 ).

=0.05 =0.05,

Показатели качества, время регулирования tрег не удовлетворяет заданным в условии .

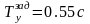
3. Оценка устойчивости замкнутой нескорректированной системы регулирования по критерию Гурвица

Характеристическое уравнение для САУ имеет следующий вид:

,

Составим определитель Гурвица: 0.665 125 0 0.0033 1 0 0 0.665 125

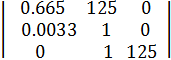
1)0.665>0

2) 0.6650 125.0000 0.0033 1.0000 0.2525>0

3) 0.6650 125 0 0.0033 1 0 0 0.6650 125 31.5625 >1

САУ по критерию Гурвица - устойчива, так как все диагональные миноры положительны.

4. Оценка устойчивости замкнутой системы по критерию Михайлова

Характеристическое уравнение для САУ имеет следующий вид:

,

В системе Matlab построим годограф Михайлова.

Текст программы:

num=[0.0033 0.665 1 125];den=[1];

w=0.0001:0.01:30;

apk=freqs(num,den,w);

u=real(apk);

v=imag(apk);

plot(u,v);grid

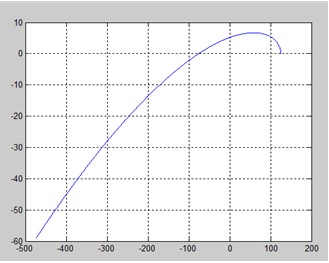
Рис.3. Годограф Михайлова.

Видно, что система устойчива, так как при изменении частоты ω от 0 до +∞,начав движение из точки, лежащей на положительной вещественной полуоси, вращаясь против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов, повернувшись угол 3·(π/2).

5. Оценка устойчивости замкнутой системы по критерию Найквиста

Устойчивость замкнутой системы определяем по АФХ разомкнутой. Сначала определим устойчивость разомкнутой системы по критерию Гурвица. Определим характеристическое уравнение разомкнутой системы:

Составим определитель Гурвица.

0.665 0 0

0.0033 1 0

0 0.665 0

0.665 >0

0.665 0 =0.665>0 0.0033 1

∆3=0.665 0 0 =0 0.0033 1 0 0 0.665 0

Так как последний определитель равен 0 , то разомкнутая система находиться на границе устойчивости, и при построении графика его необходимо дополнить дугой до положительной вещественной полуоси. И для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала точку с координатами (-1; j0).

num=[125];

den=[0.0033 0.665 1 0];

w=5:0.1:1000;

APK=freqs(num,den,w);

u=real(APK);

v=imag(APK);t=0:pi/100:2*pi;

x=sin(t);

y=cos(t);

plot(u,v,x,y);grid

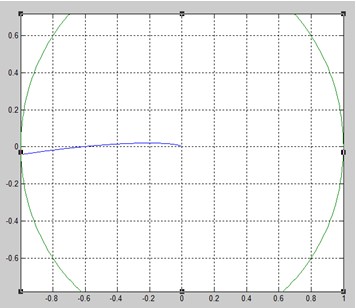
Рис.4. АФХ разомкнутой системы с указание запасов устойчивости.

Замкнутая система устойчивая т.к. разомкнутая система не охватывает точку (-1; j0).

Оценка запаса устойчивости замкнутой системы по АФХ разомкнутой системы.

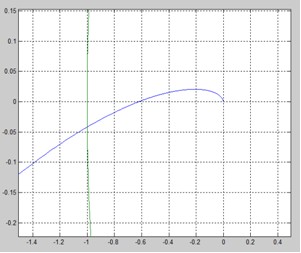
Рис.5. увеличенное АФХ разомкнутой системы с указание запасов устойчивости.