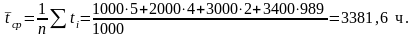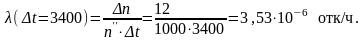- •События и их возможные исходы
- •Функции распределения случайных величин
- •Количественные показатели надёжности
- •Восстанавливаемые элементы
- •Показатели долговечности
- •Показатели ремонтопригодности
- •Показатели сохраняемости
- •Комплексные показатели надёжности
- •Математическая модель внезапного отказа
- •Анализ закономерностей, описывающих процессы изнашивания, старения и усталостного повреждения деталей и узлов локомотивов
- •Понятие о параметрической надёжности
- •Требования к информации о надёжности, методы её сбора, анализа и автоматизации
- •Характеристика исходных предпосылок оптимизации межремонтных пробегов
- •Модель оптимизации межремонтного периода исходя из экономической целесообразности
- •Управление надёжностью локомотивного парка депо
- •Технические особенности обеспечения надёжности локомотивного парка
Количественные показатели надёжности
Перед тем как говорить о показателях надёжности, необходимо уяснить, что эти показатели несколько отличаются в зависимости от того, является объект восстанавливаемым или нет. Мы уже говорили, что в процессе использования технического объекта по назначению могут возникать повреждения и отказы. Процесс обнаружения и устранения последствий отказа с целью перевода объекта из неработоспособного состояния в работоспособное состояние, называется восстановлением. Ремонт – это один из способов восстановления исправности или работоспособности изделий. Своевременное проведение ремонтов и обслуживаний позволяет во многом предупредить возникновение отказов и повреждений в течение непосредственного использования систем по назначению. При этом, если имеется в виду устранение отказа системы путём проведения ремонта, то система является восстанавливаемой. Например, локомотив, дизель, тяговый электрический двигатель – это восстанавливаемые технические системы, а сгоревшая сигнальная лампочка, вышедший из строя подшипник, триод или тиристор – это невосстанавливаемые элементы, работающие до первого отказа.
Для невосстанавливаемых элементов свойство надёжности, безотказности и долговечности совпадают. В то время как, для восстанавливаемых объектов или систем безотказность является одним из свойств, характеризующих их надёжность.
При
проведении испытаний или эксплуатации
невосстанавливаемых элементов после
наработок
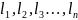 могут возникать отказы. Отказ любого
элемента вызывается действием целого
ряда факторов, большинство из которых
имеет случайный характер (качество
исходного материала, качество изготовления
и сборки, режимы работы, условия
эксплуатации и т.д.). Поэтому длительность
работы элемента до отказа, определяемая
моментом наступления отказа, будет
величиной случайной.
могут возникать отказы. Отказ любого
элемента вызывается действием целого
ряда факторов, большинство из которых
имеет случайный характер (качество
исходного материала, качество изготовления
и сборки, режимы работы, условия
эксплуатации и т.д.). Поэтому длительность
работы элемента до отказа, определяемая
моментом наступления отказа, будет
величиной случайной.
По мере наступления отказов невосстанавливаемых элементов их число в наблюдаемой выборке будет, естественно, уменьшаться.
При
испытании или в условиях эксплуатации
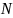 восстанавливаемых элементов также
могут возникать отказы после наработок
, но отказавшие элементы проходят
восстановление работоспособности.
Поэтому число их в наблюдаемой выборке
поддерживается неизменным, так что
число отказов
восстанавливаемых элементов также
могут возникать отказы после наработок
, но отказавшие элементы проходят
восстановление работоспособности.
Поэтому число их в наблюдаемой выборке
поддерживается неизменным, так что
число отказов
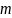 может быть и больше, чем число наблюдаемых
элементов
.
может быть и больше, чем число наблюдаемых
элементов
.
Учитывая эти особенности, рассмотрим основные количественные показатели безотказности раздельно для невосстанавливаемых и восстанавливаемых элементов.
ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ
НЕВОССТАНАВЛИВАЕМЫЕ ЭЛЕМЕНТЫ И СИСТЕМЫ
В качестве количественных показателей безотказности используются: вероятность безотказной работы, средняя наработка до отказа, интенсивность отказов.
Для
определения указанных показателей
безотказности необходимо располагать
информацией о законе распределения
наработки до отказа интересующего нас
элемента конструкции. В свою очередь,
любое распределение может быть
представлено в виде плотности распределения
(плотности вероятности) наработок до
отказа
![]() или интегральной функции (вероятности)
распределения наработок до отказа
или интегральной функции (вероятности)
распределения наработок до отказа
![]() .
Как известно, указанные характеристики
очень тесно связаны между собой.
.
Как известно, указанные характеристики
очень тесно связаны между собой.
Если
известна функция плотности распределения
,
то можно найти вероятность появления
отказа при наработке
![]() ,
не превышающей требуемой наработки
,
не превышающей требуемой наработки
![]()
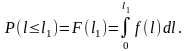
Р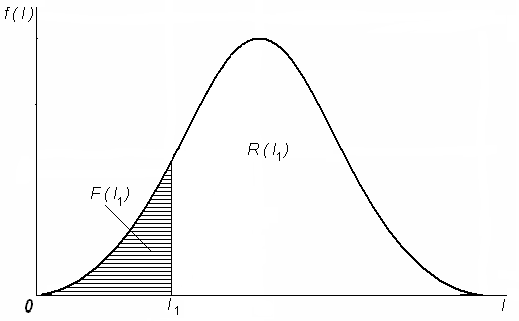 ис.4.1.
Представление вероятности отказа и
вероятности безотказной работы с помощью
плотность распределения наработки
объекта до отказа
ис.4.1.
Представление вероятности отказа и
вероятности безотказной работы с помощью
плотность распределения наработки
объекта до отказа
Полученное
соотношение можно истолковать графически.
Вероятность появления отказа за наработку
,
меньшую требуемой
,
равна относительной площади под кривой
распределения
слева от значения
(см. заштрихованную часть на рис. 4.1). Но
в таком случае, естественно, та часть
площади, которая осталась не заштрихованной,
представляет противоположную
характеристику, которую можно обозначить,
например,
![]() и
назвать вероятностью безотказной работы
изделия при наработке
.
и
назвать вероятностью безотказной работы
изделия при наработке
.
Полагая, что элемент в одно и то же время может находиться только в одном состоянии, можно записать
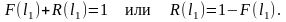
Отсюда
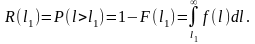
Таким образом, вероятность безотказной работы или функция надёжности – это вероятность того, что в пределах заданной наработки, например , отказа объекта не произойдёт.
В свою очередь плотность распределения
 можно выразить через функции
и
можно выразить через функции
и
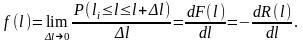
Средняя наработка до отказа – это математическое ожидание времени безотказной работы объекта или элемента. Эта характеристика также находится с помощью плотности распределения
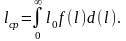
Но,
поскольку
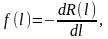
тогда
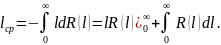
Нетрудно видеть, что первое слагаемое в этом выражении равно нулю, тогда
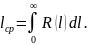
Таким
образом, средняя наработка на отказ
численно равна площади под кривой
вероятности безотказной работы
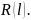
Часто
для наглядности интегральные функции
и
представляют в виде разнонаправленных
кривых, как показано на рис. 4.2. При
заданной наработке
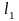 кривые дадут две вероятности (два числа):
кривые дадут две вероятности (два числа):
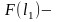 появления
отказа и
появления
отказа и
 вероятности
безотказной работы при
вероятности
безотказной работы при
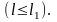
Р ис.
4.2. Интегральная функция вероятности
отказа
ис.
4.2. Интегральная функция вероятности
отказа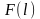 (кривая
ненадёжности) и кривая вероятности
безотказной работы
(кривая
ненадёжности) и кривая вероятности
безотказной работы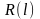 ,
характеризующая надежность элемента
при наработке
,
характеризующая надежность элемента
при наработке
![]()
С
увеличением наработки элемент или
объект объективно становится менее
надёжным. За величину, характеризующую
надёжность элемента в каждый конкретный
момент времени или наработки, принимают
отношение числа элементов, отказавших
в единицу времени, к тому количеству
элементов, которые в этот момент времени
продолжают исправно работать. Эту
величину называют интенсивностью
отказов и обозначают
![]() .
.
Интенсивность отказа есть не что иное, как отношение «скорости» изменения вероятности отказа элемента к вероятности безотказной работы элемента в заданный момент времени
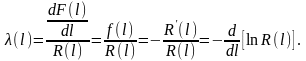
В
терминах теории вероятностей
 есть
плотность условной вероятности отказа
в момент
есть
плотность условной вероятности отказа
в момент
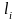 при условии, что до этого момента времени
элемент работал безотказно.
при условии, что до этого момента времени
элемент работал безотказно.
Интегрируя
приведенное выше выражение от нуля до
,
и учитывая, что
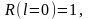 получаем
получаем
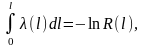
откуда
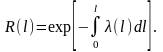
Таким образом, интенсивность отказов и вероятность безотказной работы являются характеристиками безотказности, связанными взаимно-однозначными соответствиями. Кроме того, если известна или задана функция , то тем самым, можно считать, задана не только функция , но и функция , поскольку
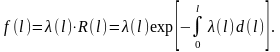
Учитывая, что приведенные выше преобразования, являются взаимообратными, можно считать, что функция содержит ту же информацию о случайной величине наработки до отказа, что и функция плотности распределения .
Р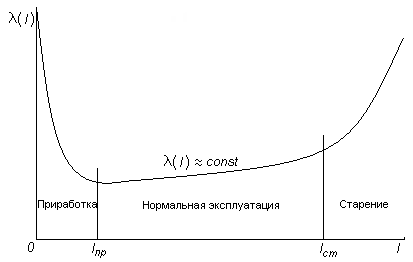 ис.
4.3. Изменение функции
по мере увеличения наработки элемента
ис.
4.3. Изменение функции
по мере увеличения наработки элемента

Типичный вид изменения функции интенсивности отказов по мере увеличения наработки элемента, приведен на рис. 4.3.
Ясно различимы три периода. Период приработки элемента, период нормальной эксплуатации и период старения.
Приведенные выше выражения позволяют рассчитывать точные значения показателей безотказности. Но для этого, как было сказано вначале, необходимо располагать информацией о виде закона распределения наработки невосстанавливаемых элементов до отказа. Когда такой информации нет, то можно, для расчета интересующих нас показателей безотказности, воспользоваться статистическими оценками этих показателей.
С
этой целью для испытуемых или наблюдаемых
в эксплуатации элементов отмечаются
их наработки до отказа или до конца
наблюдений
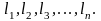
Тогда
статистическая вероятность появления
отказа
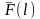 при интересующей нас наработке
при интересующей нас наработке
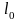 ,
когда отказало
,
когда отказало
 элементов и сохранило работоспособность
элементов и сохранило работоспособность
 элементов, равна
элементов, равна
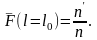
Вероятность безотказной работы

Величина средней наработки до отказа
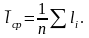
Интенсивность отказов, соответствующая достаточно малой наработке
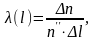
где
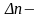 число элементов, отказавших за время
наработки
число элементов, отказавших за время
наработки
![]() ;
;
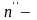 число
элементов, сохранивших работоспособность
к началу рассматриваемого промежутка
наработки
число
элементов, сохранивших работоспособность
к началу рассматриваемого промежутка
наработки
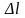 .
.
Таким образом, приближённо интенсивность отказов – это отношение среднего числа отказов элементов за единицу наработки , отнесённых к количеству элементов, оставшихся работоспособными.
Пример.
Необходимо рассчитать количественные
значения показателей безотказности
партии тиристоров в количестве
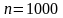 шт., которые должны иметь наработку
шт., которые должны иметь наработку
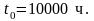 За время проведения испытаний в течение
10000 ч отказало 37 тиристоров при следующих
наработках:
За время проведения испытаний в течение
10000 ч отказало 37 тиристоров при следующих
наработках:
0
– 1000 ч отказало 5 тиристоров
![]()
1000
– 2000 ч отказало 4 тиристора
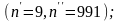
2000
– 3000 ч отказало 2 тиристора

3000
– 3400 ч отказал 1 тиристор

3400
– 5200 ч отказало 4 тиристора
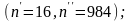
5200
– 6400 ч отказало 6 тиристоров
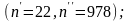
6400
– 8600 ч отказало 8 тиристоров

8600
– 10000 ч отказало 7 тиристоров
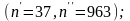
Определим величины статистических оценок показателей безотказности тиристоров.
1. За весь период проведения испытаний:

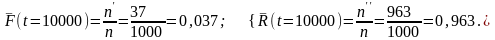

2. За период от 0 до 3400 ч