
- •1. Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(X) и ее производные .
- •2.Порядком дифференциального уравнения называется порядок нyивысшей производной, входящей в уравнение:
- •10.Если правая часть f(X) имеет вид: , где Pn(X)–многочлен n–ой степени; Qm(X)-многочлен m–ой степени.
- •Признак Лейбница.
Признак Лейбница.
Если
для знакочередующегося ряда
b1-b2+b3-b4+…(bn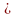 0)
выполняются условия:
0)
выполняются условия:
1. b1 b2 b3 b4…;
2.
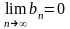 ,
- то данный ряд сходится условно.
,
- то данный ряд сходится условно.
При
этом 0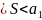 ,
а остаток
,
а остаток
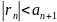
Ряд,
удовл. Условию теоремы Лейбница, наз
рядом Лейбница. Неравенство
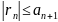 дает оценку остатка ряда Лейбница. В
частности он определяет число слогаемых,
необходимых для того, чтобы найти мумму
данного ряда с заданной точностью
дает оценку остатка ряда Лейбница. В
частности он определяет число слогаемых,
необходимых для того, чтобы найти мумму
данного ряда с заданной точностью
 .
.
21. Ряд U1+U2+..+Un+..= (1) называется функциональным, если его члены являются функциями от Х. Рассмотрим функциональный ряд U1(Х)+U2(Х)+..+Un(Х)+...(1) Совокупность тех значений Х, при которых функциональный ряд сходится, называют областью сходимости этого ряда.
Признаки
Д’Аламбера и Коши:
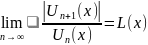
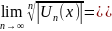 L(x)
L(x)
Фун-ый
ряд (1)сх-ся абс., если L(x)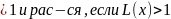 .
.
Фун-ый
ряд (1) наз равномерно сх-ся в некоторой
обл Д ф-ии S(x)
, если для
сущ.
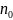 завис. от
только и не завис. от х такой, что
неравенство
завис. от
только и не завис. от х такой, что
неравенство
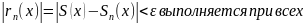 n
n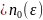 .
.
Признак
Вейерштрасса:если ряд (1) удовл. Неравенству
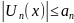 при любых из области сх-ти и знакопол.
ряд
сх-ся. То ряд (1) сх-ся равномерно.
при любых из области сх-ти и знакопол.
ряд
сх-ся. То ряд (1) сх-ся равномерно.
Свойства:
Если ряд (1) с непрер. Членами сх-ся на
множестве Д , то нго сумма S(x)
непрерывна на Д. Если ряд (1) с
непрерыв.фун-ми
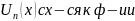 S(x)
равномерно на отр. Ab то
его можно почленно интег-ть .
S(x)
равномерно на отр. Ab то
его можно почленно интег-ть .
 .
Если ряд (1) с непрер. Диф-ми на отр. ab
фун-ми
.
Если ряд (1) с непрер. Диф-ми на отр. ab
фун-ми
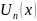 сх-ся к сумме S(x),
а ряд из производных
сх-ся к сумме S(x),
а ряд из производных
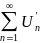 сх-ся
на этом отрезке равномерно, то и сам
ряд (1) сх-ся на ab равномерно,
а его сумма S(x)
–непрер.диф-ая ф-ия, для кот. выпол.
сх-ся
на этом отрезке равномерно, то и сам
ряд (1) сх-ся на ab равномерно,
а его сумма S(x)
–непрер.диф-ая ф-ия, для кот. выпол.
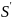 (x)=
(x)=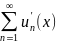 .
.
22.
Ряд вида
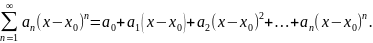 наз степенным рядом.
наз коэф. степ. ряда. При
=0 получаем ряд
наз степенным рядом.
наз коэф. степ. ряда. При
=0 получаем ряд
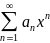 .
.
Т. Абеля: 1)Если степенной ряд сходится при значении X=X0≠0, то он сходится при всех значениях Х таких что |Х|<|X0|,2)Если степенной ряд расходится при Х=Х1, то он расходится при всех значениях Х таких что |Х|>|Х1|.
Из теоремы Абеля следует, что сущ. Такое число R≥0, что при │Х│<R ряд сходится, а при │Х│>R – расходится. Число R получило название радиуса сходимости, а интервал (-R;R)-интервала сходимости степенного ряда.
Свойства: степенной ряд сх-ся абс. и равномерно на любом отрезке внутри его интервала сх-ти. На любом отрезке [a,b], целиком принадлежащем интервалу сходимости(-R;R) степенной ряд можно почленно интегрировать и дифференцировать на этом отрезке. Степенные ряды сход к фун S(x), которая непрерывна в обл сходимости.
23.
Ряд вида
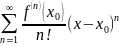 наз рядом Тейлора f(x)
в окрест.т
.
Если
наз рядом Тейлора f(x)
в окрест.т
.
Если
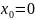 ,
то получаем ряд Маклорена:
,
то получаем ряд Маклорена:
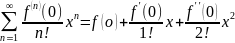
РядТейлора представляет данную ф-цию
тогда и только тогда, когда
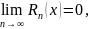 где
где
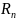 -остаточный член ф-лы Тейлора и
-остаточный член ф-лы Тейлора и
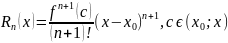 .
Если для любых
.
Если для любых
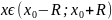 все призв.
ф-ции ограничены одной и той же
константой M , то ряд Тейлора сходится
к ф-ции в
интервале
все призв.
ф-ции ограничены одной и той же
константой M , то ряд Тейлора сходится
к ф-ции в
интервале
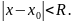 Если степенной ряд по степеням
Если степенной ряд по степеням
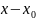 сходится к ф-ции f(x) в
окрестности точки
сходится к ф-ции f(x) в
окрестности точки
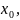 то он является рядом Тейлора ф-ции
f(x) в
oкрестности этой точки.
то он является рядом Тейлора ф-ции
f(x) в
oкрестности этой точки.
Разложение в ряд Маклорена ф-ции ex, cos x, sin x
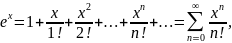
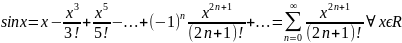
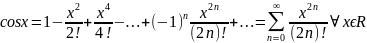
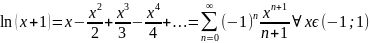
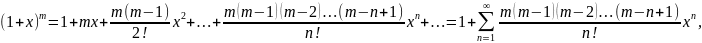
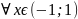
24. Периодическая ф-ия- ф-ия, описыв.
период. процесс представ-ся каксумма
конеч. или бескон. числа простых период.
ф-ий (гармоник). Asin(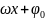 ).
Каждый гармоник можно предс. в виде
acos
).
Каждый гармоник можно предс. в виде
acos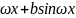 . Сумма, разность, произвед. част.
период-их ф-ий также явл. период. ф-ями.
. Сумма, разность, произвед. част.
период-их ф-ий также явл. период. ф-ями.
Две ф-ии
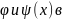 пространстве L2 наз
ортогональным на отр.ab,
если их скалярное произведение на
отр.=0
пространстве L2 наз
ортогональным на отр.ab,
если их скалярное произведение на
отр.=0
(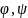 )=
)=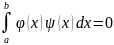
Ортог.с-ма ф-ии
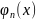 на
отр.ab наз. нормированной.
если норма
на
отр.ab наз. нормированной.
если норма
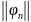 =1.
=1.
Полное. Бесконечное эвклидово
простр.наз.Гильберттовым, т.е.гил-во
простр.Н есть совокуп.элементов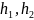 …любой
природы, удовл.усл.:1.Н есть эвклидово
простр.Н-полно в смысле метрики
…любой
природы, удовл.усл.:1.Н есть эвклидово
простр.Н-полно в смысле метрики
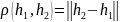
Пусть f(x)
заданоина промежутке
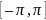
f(x) =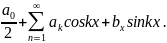 Будем полагать, что правая састь
уравн.сх-ся равномерно, тогда:
Будем полагать, что правая састь
уравн.сх-ся равномерно, тогда:
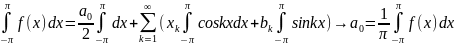 ,
,
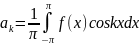
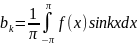
Достат. усл разлож. ф-ии ряда Фурье явл.
теорема Дирихле: если 2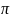 -
период.ф-ия кусочногл.на (-
-
период.ф-ия кусочногл.на (-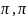 ),
то ее ряд Фурье сх-ся к f(x)
в каждой точке ее непрер. и к значению
),
то ее ряд Фурье сх-ся к f(x)
в каждой точке ее непрер. и к значению
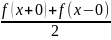 ,
где х- точка первого рода, т.е.
,
где х- точка первого рода, т.е.
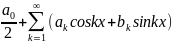 ,
при х=
,
при х=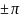 сумма ряда Фурье равна:
сумма ряда Фурье равна:
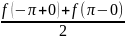 . Если же f(x)
кусочногл.и непрерыв., то ряд Фурье
сх-ся к f(x)
равномерно. cosk
. Если же f(x)
кусочногл.и непрерыв., то ряд Фурье
сх-ся к f(x)
равномерно. cosk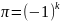 .
.
26. Если f(x)-четное,
то f(x)coskx-
четное,а f(x)sinkx-нечетное.
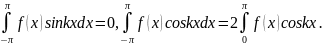 В этом случае
В этом случае
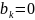 ,
,
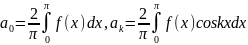 .
.
F(x)-нечетное, тогда f(x)sinkx-четное,а f(x)coskx-нечетное.
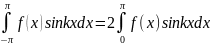 ,
, .
.
Может оказаться, что ф-ия f(x)
задана на отр.[0,
]и
требуется разл.эту ф-ию в ряд Фурье на
отр
.Тогда
зад-ую ф-ию f(x)на
.[0,
]
тем или иным образом доопределяют на
отр.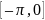 .
Ряды по cos-ам и sin-ам.
.
Ряды по cos-ам и sin-ам.
27.Устоновим, что для 2 период. ф-ии среди всех тригономет. многочленов
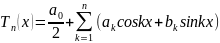 найменшее сред. ариф. отклонение от
f(x) имеют
многочлен
найменшее сред. ариф. отклонение от
f(x) имеют
многочлен
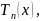 коэф.кот.
коэф.кот.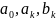 есть коэф. Фурье для ф-ии f(x).
Это св-во наз. экстремальным св-ом коэф.
Фурье испол.для приближ.представ.период-их
ф-ий в виде тригонометрич.многочленов.
есть коэф. Фурье для ф-ии f(x).
Это св-во наз. экстремальным св-ом коэф.
Фурье испол.для приближ.представ.период-их
ф-ий в виде тригонометрич.многочленов.
f(x)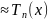 .
.
Аналог ряда Фурье- интеграл Фурье, который дает разложение ф-ии по непрерыв.спектру частот.С помощью интег.Ф-ье, ряд Ф-ье переходит в преобразование Ф-ье и ф-ию f(x) предст. в виде непрерыв.совокуп.простейших ф-ий.
Достаточные условия предст.Ф-ье в ряд Ф-ье явл.след.ф-ии:
1-f(x) определена на всей оси OX и кусочнонепрер.на всех Ox.
2.f(x) абс-но
интег-ма на всей числовой прямой (-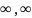 ).
).
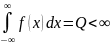 .
.
3. На любом конеч. отрезке [-l,l] ф-ия кусочногл.
4.В точках непрерыв.интеграл Ф-ье определяется самой ф-ией f(x). А в точках разрыва полусуммой левосторон. и правостор. предела ф-ии в этих точках.
На любом конечном отрезке [-l,l]
f(x) предс-ся
рядом Ф-ье: f(x)=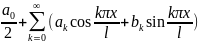 ,
,
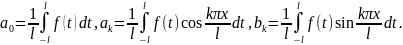
f(x)=
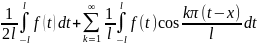
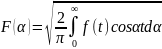 наз. интегралом косинус преобр.Ф-ье для
f(x), а Ф(
наз. интегралом косинус преобр.Ф-ье для
f(x), а Ф(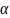 )=
)=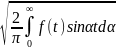 наз.синус преобразования Ф-ье.
наз.синус преобразования Ф-ье.
28. Комп.числом z наз.упорядоченную пару чисел z=(x,y) если y=0, то z=(x,0)=0 получ.действит.числа, при x=0 получ.z=(0,y), эти числа наз.мнимыми числами.
Алгебраичная
форма:z=x+iy.Знаки
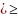 не прииен-ся.
не прииен-ся.
Тригонометр.форма:z=x+iy=rcos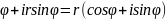
Показательная
форма: z=r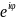 .
.
Плоскость на кот.изоьр.компл-ые числа наз.компл.плоскостью и обознач.буквой С.
29.Множ.,состоящее из внутр.точек,наз.открытым. Множество,состоящее из внутр. и грнич.точек наз.замкнутым и обознач. буквой Д. Множество наз.связным, если любая нго точка А может быть соединена с др.т В непрерывной кривой или ломаной полностью располож.в этом множестве.Областью на комп.плоск.наз.всякое открытое связанное множество.
КП
w=f(z)
наз.ф-ей КП z опрелен-ой
на множ. Д. если по некот.правилу и закону
каждому знач.z принадл-ему,
Д ставится в соответ.одно или некот.
совокуп. значение w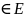 .
.
Число
А=a+bi наз.
пределом ф-ии f(z)
точки
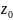 если для любого
если для любого
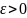 сущ.
сущ.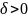 т.что для всех z
т.что для всех z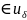 выпол.неравенсто:
выпол.неравенсто: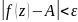 ,
A=
,
A=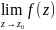 .
Ф-ия f(z)
определ-ая в некот. окрестности
наз.непрерыв.в т.
если
.
Ф-ия f(z)
определ-ая в некот. окрестности
наз.непрерыв.в т.
если
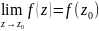 .
.
30.Степенная
ф-ия
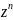 это однознач. ф-ия опред-ая и непрерыв.на
всей расширенной плоскости
это однознач. ф-ия опред-ая и непрерыв.на
всей расширенной плоскости
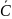 .
.
Целая
рац-ая ф-ия w=f(z)=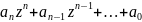 ,
также однозн.ф-ия определ., непрерыв.на
.
,
также однозн.ф-ия определ., непрерыв.на
.
Дробно-рац-ая:
w=f(z)=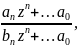 однозн.,определ
и непрерыв. На всей
за исключ.точек, в кот.знамен.оьращ.в
ноль.
однозн.,определ
и непрерыв. На всей
за исключ.точек, в кот.знамен.оьращ.в
ноль.
Показательная:
w=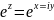 =
=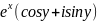 .
.
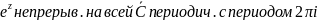
Тригонометрическая:
sinz=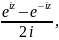 cosz=
cosz=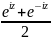 ,
,
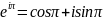 .
.
Гиперболич.:sinz=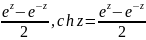 .
.
31.Логприфм-ая, w=Lnz,обратная для показательной ф-ии. W= Lnz=ln|z|+i(argz+2k )-многозначная ф-ия.
Степен.w=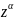 где
z –ком.перем.,
-ком.число.
w=
где
z –ком.перем.,
-ком.число.
w=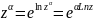 .
.
Показат.:w=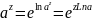 -многозн.ф-ия.
-многозн.ф-ия.
Обр.тригоном.:z=sinw=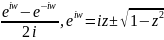 ,
w=Arcsinz=-iLn(iz
,
w=Arcsinz=-iLn(iz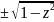 ),w=Arccosz=iLn(z
),w=Arccosz=iLn(z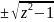 ).
).
Обр.гипербол.ф-ии:w=Arcshz=Ln(z+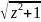 ),w=Arcchz=Ln(z+
),w=Arcchz=Ln(z+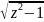 )
,w=Atcthz=
)
,w=Atcthz=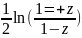 ,w=Arccthz=
,w=Arccthz=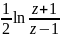 .
.
32.Ф-ию f(z), имеющуу в т. Z0 производ.наз. диф-ой (монотонной)
F(z0+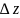 )-f(z0)=
)-f(z0)=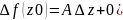 ,
,
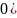 -необх.
и достаточ. Условие диф-ти ф-ии f(z)в
т. Z0.A=
-необх.
и достаточ. Условие диф-ти ф-ии f(z)в
т. Z0.A=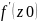
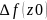 =
=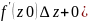 ,
Условие Коши-Римона:
,
Условие Коши-Римона: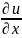 =
=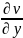 ,
,
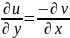 ,
для показ-ой формы:z=r
.
,
для показ-ой формы:z=r
.
Ф-ия
w=f(z)
наз.аналит. т.z0 ,если она
диф-ема в самой т.z0 и в
некот.окрестн.этой точки. Уравнение
Лапласа: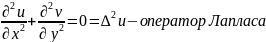 .
Ф-ии, удовлет. Уравн.Лапласа, наз.
гармонические.
.
Ф-ии, удовлет. Уравн.Лапласа, наз.
гармонические.
33.Производная
ф-ии f(z) в
т.z0 наз.число
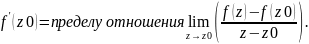 если
этот предел сущ-ет.
если
этот предел сущ-ет.
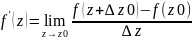
K=|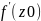 |=
|=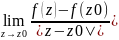 .
Геометр-ий смысл модуля в том, что
он равен коэф-ту растяж.бесконечномалых
векторов в т.z0 при
отображ.w=f(z)
и не зависит от вида и направл.кривой,
но кот.перемещ.т.z в
плоскости z.Если
.
Геометр-ий смысл модуля в том, что
он равен коэф-ту растяж.бесконечномалых
векторов в т.z0 при
отображ.w=f(z)
и не зависит от вида и направл.кривой,
но кот.перемещ.т.z в
плоскости z.Если
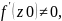 то
угол поворота в т. Z0 не
зависит от кривой и равен arg
,
т.е. все кривые, прох-ие через т.z0
на плоск.z повор-сяпри
отобр.w=f(z)на
один и тот же угол= arg
-в
этом состоит геометр.смысл аргумента
произв.аналит.ф-ии.
то
угол поворота в т. Z0 не
зависит от кривой и равен arg
,
т.е. все кривые, прох-ие через т.z0
на плоск.z повор-сяпри
отобр.w=f(z)на
один и тот же угол= arg
-в
этом состоит геометр.смысл аргумента
произв.аналит.ф-ии.
34.Ф-ия w=f(z)отобр-ет плоск.обл.Д на комп.плоск.в некотор.множ.точек комп.плоск.w.Отображение одной плоск.на другую наз.комформным в т.z, если все бесконечномалые дуги,вых-ие из этой точки при отображ.поворач-ся на один и тот же угол и получают одно и то же растяжение.
Линейная
ф-ия w=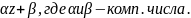 1-z1=
1-z1=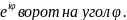
2-z2=rz1,3-z3=z2+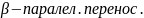
Дробнолин-ая
ф-ия w=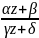 ,
,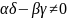 .
.
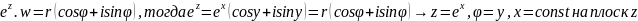 –окружность, y =const-лучи,
–окружность, y =const-лучи,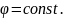
35.Если
сущ.конеч.предел интег-ой сумм Sn
при
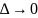 незав-ый
ни от способа разбиения кривой, ни от
выбора точек
незав-ый
ни от способа разбиения кривой, ни от
выбора точек
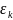 то этот предел наз.интегралом ф-ии
f(z)по кривой
l.
то этот предел наз.интегралом ф-ии
f(z)по кривой
l.
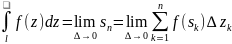 ,интеграл
по разамкнутому контуру:
,интеграл
по разамкнутому контуру: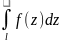 =
=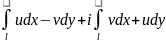 .
.
Св-ва:Линейность
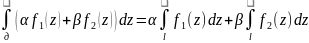 Адетивность: если l=
Адетивность: если l=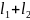 то
то
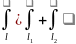 .
.
36.
Теорема Коши для односв.обл.:Если
f(z)-аналит.ф-ия
в односв.обл.Д, то интеграл, взятый вдоль
любого замк-го кусочногл.контура
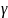 целиком принадл-го обл.Д=0.
целиком принадл-го обл.Д=0.
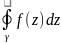 =0.Для
любой внут.т.z0 f(z0)=
=0.Для
любой внут.т.z0 f(z0)=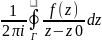
Для
многосв.обл.:Пусть f(z)
аналит.ф-ия в замк.многосв.обл.Д с
границей Г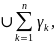 где
Г-внеш.контур обл.Д, а
где
Г-внеш.контур обл.Д, а
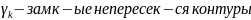 ,
тогда
,
тогда
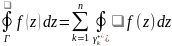 .
Для любой внут.т.z0 f(z0)=
.
Для любой внут.т.z0 f(z0)=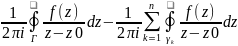
37. Исслед-ие рядов можно свести к исслед-ию соответ.числовых рядов действител.чисел.
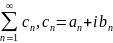 ,
,
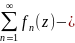 функц-ый
ряд. Ряд наз.сх-мся, если сущ.
функц-ый
ряд. Ряд наз.сх-мся, если сущ.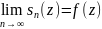 .Функ-ый
ряд наз.равномерносх-мся в обл.д его
сх-сти к сумме f(z),
если можно указать номер N=N(
)
что при всех n
.Функ-ый
ряд наз.равномерносх-мся в обл.д его
сх-сти к сумме f(z),
если можно указать номер N=N(
)
что при всех n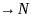 выпол.неравен.
выпол.неравен.
|f(z)-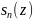 =|
=|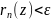 ||
для
||
для

Числовой ряд:
Степенной ряд: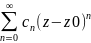 .
Степ.ряд сх-ся при |z-z0|
.
Степ.ряд сх-ся при |z-z0|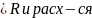 при |z-z0|
при |z-z0|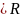 .
R=
.
R=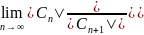
38. f(z)=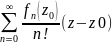 =f(z0)+
=f(z0)+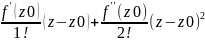 -
ряд Тейлора. Ряд справа сх-ся в круге
|z-z0|
-
ряд Тейлора. Ряд справа сх-ся в круге
|z-z0|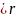 ,
если z0=0. То получим ряд
Маклорена. Ряд Лорана содержит и полож.и
отриц.степ.z-z0
и в которой расклад.аналит. в кольце
R
,
если z0=0. То получим ряд
Маклорена. Ряд Лорана содержит и полож.и
отриц.степ.z-z0
и в которой расклад.аналит. в кольце
R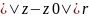 ,
f(z)=
,
f(z)=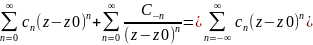 -ряд
Лорана.
-
правильная часть р.Лорана, кот.сх-ся в
круге|z-z0|
и
-ряд
Лорана.
-
правильная часть р.Лорана, кот.сх-ся в
круге|z-z0|
и
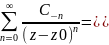 главная
часть р.Лорана, кот сх-ся во внеш.части
круга |z-z0|
.
главная
часть р.Лорана, кот сх-ся во внеш.части
круга |z-z0|
.
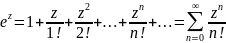
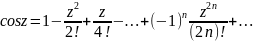
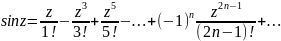
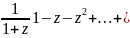
Ln(1+z)=z-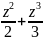 -…(
-…(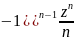
39. Нули, особые точки f(z)
наз.изолиров., если каж. из них мож.окружить
непересек-ся окружн.сколь малыми они
бы не были.Изолир.особые точки:1-устраним.
особая точ. 2-полюс. 3-существенноособая
точка. z0- устран.точка,если
сущ.конеч.предел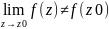 ,
z наз. полюсом, если
,
z наз. полюсом, если
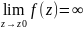 ,
z0 наз.сущест.особой
точкой.если
,
z0 наз.сущест.особой
точкой.если
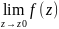 не сущ-ет.
не сущ-ет.
Ряд Лорана : f(z)=
)=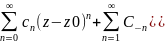 .
.
40. Вычетом ф-ии f(z)
относ-но особой точки z0
наз.коэф-т
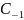 при слогаемом, содержащ.
при слогаемом, содержащ.
 разложение ф-ии в ряд Лорана. Resf(z)при
z=z0 равен
.
отличен от нуля, только если z0полюс
или сущ.лслбая точка. Т. образом Resf(z)=
разложение ф-ии в ряд Лорана. Resf(z)при
z=z0 равен
.
отличен от нуля, только если z0полюс
или сущ.лслбая точка. Т. образом Resf(z)=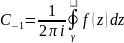 .
Устранимая особая точка вычет имеет:
Resf(z)при
z=z0=
.
Устранимая особая точка вычет имеет:
Resf(z)при
z=z0=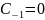 .
Если z0- полюс порядка kто
вычет опред. так:
.
Если z0- полюс порядка kто
вычет опред. так:
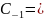 Resf(z)=
Resf(z)=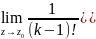
41. Пусть f(z) –аналит. ф-ия в односв.обл.Д за исключ.конеч. числа точек z1,z2… -замк-ыый положительноориен. Контур, распол-ый в обл.Д внутри которого содер.все особые точки, тогда:
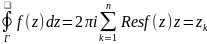
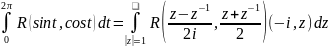
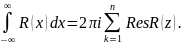
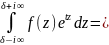 2
2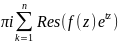 .
.
42. F(p) =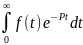 ,
завис-ий от комп.параметра P=
,
завис-ий от комп.параметра P=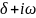 .Этот
интеграл наз.интегралом или преобр.
Лапласа ф-ии f(t).
F(p)наз.
изобр.ф-ии по Лапласу, а f(t)наз.
оригиналом.
.Этот
интеграл наз.интегралом или преобр.
Лапласа ф-ии f(t).
F(p)наз.
изобр.ф-ии по Лапласу, а f(t)наз.
оригиналом.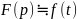 или
F(p)=L
или
F(p)=L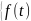 .
.
Теорема сущест-ия изобр.: любой ориг.имеет
изобр. Изобр.явл.аналит-ой ф-ей
полуплоскости Rep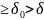 .
.
Теорема смещения:если f(t)≓F(p),
то для
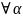 комплексных
комплексных
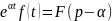 ,
где
,
где
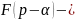 запаздывание
изобр.на
.
запаздывание
изобр.на
.
Теорема запаздывания:если
f(t)
оригинал. То f(t-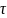 ),
),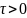 тоже оригинал с элемент.,запаздыв=им
на велич.
тоже оригинал с элемент.,запаздыв=им
на велич.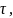 и если f(t)≓F(p)
и если f(t)≓F(p)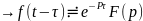
43. Если же f(t)
с периодом T
,
то его изобр. Имеет вид f(t)
≓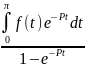 .
.
Сверткой 2-х оригин.
f1(t)
и f2(t)наз.ф-ию,кот.запис.так:
f1(t)*
f2(t)=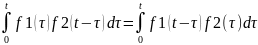 .
Свертка облад.св-ми комутат-ти. линейности
и осоциоц-ти.
.
Свертка облад.св-ми комутат-ти. линейности
и осоциоц-ти.
Теорема смещения:если f(t)≓F(p), то для комплексных , где запаздывание изобр.на .
44.Теорема Бореля: Если f1(t)
имеет изобр.F1(t)
и f2(t) ≓
F2(t),то
свертка f1(t)
 f2(t)
≓ F1(p)
F2(p)
и эта формула наз. ф-лой умножения изобр.
f2(t)
≓ F1(p)
F2(p)
и эта формула наз. ф-лой умножения изобр.
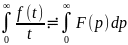
Интеграл Дюамеля: Если f1(t)
непрерыв.. а f2(t)
–непрерыв.диф. оригинал и М1(p)
и М2(p)- их изобр., то
pF1(p)F2(p)
≓
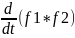 .
.
Сверткой 2-х оригин. f1(t) и f2(t)наз.ф-ию,кот.запис.так: f1(t)* f2(t)= . Свертка облад.св-ми комутат-ти. линейности и осоциоц-ти.
