Разложение булевых функций по переменным

Введем обозначение

.

Таблица 7

0	0	1
0	1	0
1	0	0
1	1	1

где - параметр, равный либо 0, либо 1. Очевидно, что

Теорема (о разложении функций по переменным, разложение Шеннона). Каждую функцию алгебры логики при любом можно представить в следующей форме:

(1)

где дизъюнкция берется по всевозможным наборам значений переменных .

Это представление называется разложением функции по переменным .

Дизъюнктивные и конъюнктивные нормальные формы

Следствия разложений.

1) Разложение по переменной .

= .

Функции и называются компонентами разложения.

2) Разложение по переменной .



3) Разложение по двум переменным и (таблица 8).

Таблица 8

0 0 0 1 1 0 1 1	0 1 1 0

   

 

.

4) Разложение по всем переменным:

. (2)

При (2) может быть преобразовано:

.

В результате окончательно получим

. (3)

Дизъюнкция по всем наборам , где .

Такое разложение носит название совершенной дизъюнктивной нормальной формы (совершенной ДНФ).

Совершенная ДНФ - это выражение типа , т. е. логическая сумма произведений . Нельзя ли для булевых функций получить разложение типа ? Покажем, что при это возможно, для чего разложим функцию (двойственная к функции ) (очевидно, ) в совершенную ДНФ:

.

Возьмем тождество для двойственных формул

.

Левая часть есть , а правая может быть преобразована далее:

.

Рассмотрим, как получается из выражения выражение .

Таким образом, получаем разложение

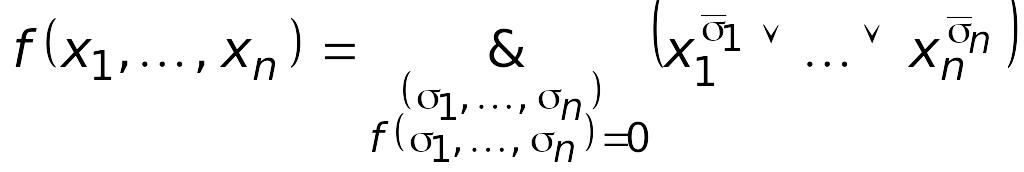. (4)

Это выражение носит название совершенной конъюнктивной нормальной формы (совершенной КНФ)

Задание функции в виде совершенной ДНФ и совершенной КНФ более компактно, чем задание функций в виде таблиц. Для пояснения рассмотрим функцию

.

Данная формула в правой части насчитывает 39 символов (20 символов переменных и 19 символов ), таблица для содержит , т. е. более миллиона строк.