Эквивалентные преобразования формул, задающих булевы функции

Определение. Формулы и над называются эквивалентными, если соответствующие им функции и равны, т. е. . Запись будет означать, что формулы и эквивалентны.

Приведем список эквивалентностей (тождеств), характеризующих свойства некоторого множества элементарных функций (главным образом множества ).

Обозначим через любую из функций , , . Существенно только, чтобы символ в тождестве имел один и тот же смысл.

1. Функция обладает свойством ассоциативности:

.

2. Функция обладает свойством коммутативности:

.

3. Для конъюнкции и дизъюнкции выполняются дистрибутивные законы:

,

.

4. Имеют место следующие соотношения между отрицанием, конъюнкцией и дизъюнкцией:

, , .

4. Выполняются следующие свойства конъюнкции и дизъюнкции:

, ,

, ,

, ,

, .

Замечания

1. С целью упрощения записи формул условимся, что операция сильнее операции , т. е. если нет скобок, то сначала выполняется операция , а потом . Например, запись означает .

2. В силу закона ассоциативности для можно вместо формул , пользоваться выражением , которое не является формулой, но может быть превращено в нее путем расстановки скобок, причем функциональные свойства не меняются, как бы ни расставляли скобки.

Иногда будем использовать следующую форму записи:

,

.

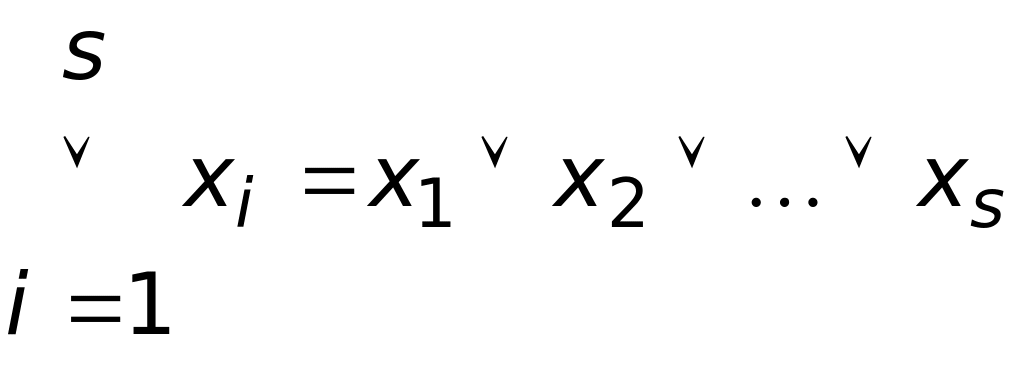В дальнейшем, используя замечания 1 и 2, будем употреблять не формулы, а выражения, отличающиеся от формул тем, что в них кое-где пропущены скобки. Эти выражения также иногда будем называть формулами.

Определение. Функция , равная , называется двойственной функцией к функции .

Таблица для двойственной функции получается из таблицы для функции инвертированием (т. е. заменой 0 на 1 и 1 на 0) столбца функции и его переворачиванием (таблица 1).

Таблица 1

		замена 1 на 0; 0 на 1	(перевор. предыд. столб.)
0 0	1	0	1
0 1	0	1	1
1 0	0	1	1
1 1	0	1	0

Среди функций

функция 0 двойственна 1,

функция 1 двойственна 0,

функция двойственна (таблица 2),

Таблица 2

0	0	1	0
1	1	0	1

функция двойственна (таблица 3),

Таблица 3

0	0	1	0
1	1	0	1

функция двойственна (таблица 4),

Таблица 4

0 0	0	1	0
0 1	0	1	1
1 0	0	1	1
1 1	1	0	1

функция двойственна (таблица 5).

Таблица 5

0 0	0	1	0
0 1	1	0	0
1 0	1	0	0
1 1	1	0	1

Из определения двойственности вытекает, что

,

т. е. функция является двойственной к (свойство взаимности).

Принцип двойственности. Если формула реализует функцию , то формула , т. е. формула, полученная из заменой функций соответственно на , реализует функцию .

Эту формулу мы будем называть формулой, двойственной к , и обозначать через . Таким образом,

.

Пример (таблица 6).

, .

Таблица 6

0 0	1	0 1	1
0 1	0	1 1	1
1 0	0	1 1	1
1 1	0	1 0	0