- •Понятие множества.
- •Операции над множествами.
- •Унарные операции
- •Свойство числовых множеств и последовательностей.
- •Свойства
- •Евклидово пространство.
- •Понятие окрестности точки.
- •Функциональная зависимость.
- •Графики и свойства основных элементарных функций.
- •Предел числовой последовательности.
- •Предел функции.
- •Основные теоремы о пределах.
- •Первый и второй замечательные пределы. (это что за хрень?))))
- •Раскрытие неопределённостей, правило Лопиталя.
- •Непрерывность функции в точке и на интервале.
- •Свойство непрерывных функций.
- •Точки разрыва первого и второго рода.
- •Нахождение асимптоты функции.
- •Порядок нахождения асимптот
- •Наклонная асимптота — выделение целой части
- •Производная и дифференциал.
- •Основные теоремы о дифференцируемых функциях.
- •Выпуклость функции.
- •Производная сложной функции.
- •Функции нескольких переменных и их неопределённость.
- •Производные функции нескольких переменных.
- •Дифференциалы функции нескольких переменных.
- •Поиск экстремума функции одной переменной.
- •Поиск экстремума функции двух переменных.
Производная сложной функции.
Двухслойная" сложная функция записывается в виде
![]()
где u
= g(x) -
внутренняя функция, являющаяся, в свою
очередь, аргументом для внешней
функции f.
Если f и g -
дифференцируемые функции, то сложная
функция ![]() также
дифференцируема по x и
ее производная равна
также
дифференцируема по x и
ее производная равна
![]()
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.
Пример
Найти
производную функции ![]() .
.
Решение.
Поскольку ![]() ,
то по правилу производной сложной
функции получаем
,
то по правилу производной сложной
функции получаем
![]()
Функции нескольких переменных и их неопределённость.
Функции двух переменных Приращение функции
![]()
Функция,
дифференцируемая в точке ![]()
![]() при
при ![]()
В этом случае дифференциал функции в точке :
![]()
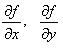 -
частные производные, вычисленные в
точке
.
-
частные производные, вычисленные в
точке
.
Дифференцирование композиции
1.
Если ![]() то
то
![]()
2.
Если ![]() то:
то:
![]()
![]()
![]()
Однородная функция степени k
![]()
Это тоже подходит?)))смотри ниже теорию
-Если
каждой упорядоченной паре чисел ![]() по
некоторому закону
по
некоторому закону ![]() поставлено
в соответствие единственное действительное
число
поставлено
в соответствие единственное действительное
число ![]() ,
то говорят, что задана функция двух
переменных
,
то говорят, что задана функция двух
переменных ![]() или
или ![]() .
Числа
.
Числа ![]() называются
при этом независимыми переменными или
аргументами функции, а число
–
зависимой переменной.
называются
при этом независимыми переменными или
аргументами функции, а число
–
зависимой переменной.
-
число![]() называется
пределом функции
при
называется
пределом функции
при ![]() (или
в точке
(или
в точке ![]() ),
если для любого сколь угодно малого
положительного числа
),
если для любого сколь угодно малого
положительного числа ![]() существует
существует ![]() (зависящее
от
(зависящее
от ![]() )
такое, что для всех
)
такое, что для всех ![]() и
удовлетворяющих неравенству
и
удовлетворяющих неравенству ![]() выполняется
неравенство
выполняется
неравенство ![]() .
.
Производные функции нескольких переменных.
Пусть f(x,
y) —
функция двух переменных x,
y,
определена в некоторой окрестности
точки (x0,
y0).
Если существует конечный предел ![]() ,то
функция f(x,
y) имеет
в точке (x0,
y0) частную
производную по переменной x. Аналогично
определяется частная производная
функции f(x1,
x2,
…, xn) по
переменной xi :
,то
функция f(x,
y) имеет
в точке (x0,
y0) частную
производную по переменной x. Аналогично
определяется частная производная
функции f(x1,
x2,
…, xn) по
переменной xi :![]() Обозначают:
Обозначают:![]() ,
,![]() .
.
Дифференциалы функции нескольких переменных.
http://rk6.bmstu.ru/electronic_book/mathematic/fun.htm
Поиск экстремума функции одной переменной.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
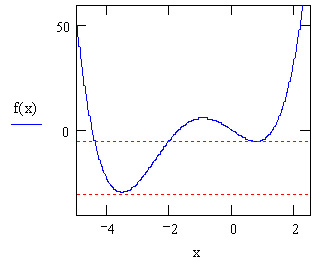
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис. 8.8 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканиро-вать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.