
- •Понятие множества.
- •Операции над множествами.
- •Унарные операции
- •Свойство числовых множеств и последовательностей.
- •Свойства
- •Евклидово пространство.
- •Понятие окрестности точки.
- •Функциональная зависимость.
- •Графики и свойства основных элементарных функций.
- •Предел числовой последовательности.
- •Предел функции.
- •Основные теоремы о пределах.
- •Первый и второй замечательные пределы. (это что за хрень?))))
- •Раскрытие неопределённостей, правило Лопиталя.
- •Непрерывность функции в точке и на интервале.
- •Свойство непрерывных функций.
- •Точки разрыва первого и второго рода.
- •Нахождение асимптоты функции.
- •Порядок нахождения асимптот
- •Наклонная асимптота — выделение целой части
- •Производная и дифференциал.
- •Основные теоремы о дифференцируемых функциях.
- •Выпуклость функции.
- •Производная сложной функции.
- •Функции нескольких переменных и их неопределённость.
- •Производные функции нескольких переменных.
- •Дифференциалы функции нескольких переменных.
- •Поиск экстремума функции одной переменной.
- •Поиск экстремума функции двух переменных.
Нахождение асимптоты функции.
Аси́мпто́та (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность[2]. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещё Архимед
Порядок нахождения асимптот
Нахождение вертикальных асимптот.
Нахождение двух пределов
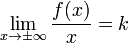
Нахождение двух пределов
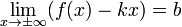 :
:
если ![]() в
п. 2.), то
в
п. 2.), то ![]() ,
и предел
ищется
по формуле горизонтальной асимптоты,
,
и предел
ищется
по формуле горизонтальной асимптоты, ![]() .
.
Наклонная асимптота — выделение целой части
Также наклонную асимптоту можно найти, выделив целую часть. Например:
Дана функция ![]() .
.
Разделив нацело числитель на знаменатель, получим:
![]() .
.
При
![]() ,
,
![]() ,
то есть:
,
то есть:
![]() ,
,
и ![]() является
искомым уравнением асимптоты.
является
искомым уравнением асимптоты.
Производная и дифференциал.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс —интегрирование.
Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции. (Δxf(Δx) = f(x + Δx) − f(x).); малое изменение величины в математическом выражении вследствие такого же незначительного изменения переменной
Для функции:
Дифференциал
функции ![]() в
точке
в
точке ![]() может
быть определён как линейная функция
может
быть определён как линейная функция
![]()
где f'(x0) обозначает производную f в точке x0.
Таким
образом df есть
функция двух аргументов ![]() .
.
Дифференциал
может быть определён напрямую, т.е., без
привлечения определения производной
как функция ![]() линейно
зависящая от h и
для которой верно следующее соотношение
линейно
зависящая от h и
для которой верно следующее соотношение
![]()
Основные теоремы о дифференцируемых функциях.
http://termech.mpei.ac.ru/kir/PDF/Lecmatem7.html
у меня не получается скопировать…ворд съезжает…..сволочь
Остальные сайты на нобелевскую премию идут))) и ставят одни формулы
Выпуклость функции.
Выпуклая функция — функция, у которой надграфик является выпуклым множеством
Вещественнозначная
функция, определённая на некотором интервале (в
общем случае на выпуклом
подмножестве некотороговекторного
пространства)
выпукла, если для любых двух значений
аргумента x, y и
для любого числа ![]() выполняется
неравенство
Йенсена:
выполняется
неравенство
Йенсена:
![]()
Если
это неравенство является строгим для
всех ![]() ,
функция называется строго
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.
,
функция называется строго
выпуклой;
если выполняется обратное неравенство,
функция называется вогнутой,
или выпуклой
вверх.

NB! Иногда выпуклая функция определяется как вогнутая и наоборот
Свойства(нужно тебе или нет, не знаю, но выглядят эти свойства очень умно)))
Функция f, выпуклая на интервале
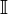 , непрерывна на
всём
, дифференцируема на
всём
за
исключением не более чем счётного
множества точек
и дважды дифференцируема почти везде.
, непрерывна на
всём
, дифференцируема на
всём
за
исключением не более чем счётного
множества точек
и дважды дифференцируема почти везде.Непрерывная функция f выпукла на тогда и только тогда, когда для всех точек
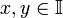 выполняется
неравенство
выполняется
неравенство
![]()
Непрерывно дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её график лежит не ниже касательной, проведённой к этому графику в любой точке промежутка выпуклости.
Дважды дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её вторая производная неотрицательна на этом интервале. Если вторая производная дважды дифференцируемой функции строго положительна, такая функция является строго выпуклой, однако обратное неверно (например, функция f(x) =x4 строго выпукла на [ − 1,1], но её вторая производная в точке x = 0 равна нулю).
Если функции f, g выпуклы, то любая их линейная комбинация af + bg с положительными коэффициентами a, b также выпукла.
Локальный минимум выпуклой функции является также глобальным минимумом (соответственно, для выпуклых вверх функций локальный максимум является глобальным максимумом).
Любая стационарная точка выпуклой функции будет глобальным экстремумом.
Для выпуклых функций выполняется неравенство Йенсена:
![]() где X — случайная
величина со
значениями в области
определения функции f, E — математическое
ожидание.
где X — случайная
величина со
значениями в области
определения функции f, E — математическое
ожидание.
