48) Критерий согласия Пирсона о предполагаемом законе распределения случайной величины

Критерий согласия Пирсона (χ²) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.

И спользование критерия χ² предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) n_j для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.

Число интервалов зависит от объема выборки. Статистикой критерия Пирсона служит величина,   где p_j - вероятность попадания изучаемой случайной величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x). При вычислении вероятности p_j нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до -∞, а последний - до +∞.

Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле величины с критическим значением χ²_α, найденным по приложения для уровня значимости α и числа степеней свободы k = e₁ - m - 1. Здесь e₁ - число интервалов после объединения; m - число параметров, оцениваемых по рассматриваемой выборке. Если выполняется неравенство χ² ≤ χ²_α   (3.92) то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.

Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ² другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).

49) Критерий согласия Колмогорова о предполагаемом законе распределения случайной величины.

Этот критерий применяется для проверки простой гипотезы Н₀ о том, что независимые одинаково распределенные случайные величины Х₁, Х₂, …, Х_п имеют заданную непрерывную функцию распределения F(x).

Найдем функцию эмпирического распределения F_n(x) и будем искать границы двусторонней критической области, определяемой условием

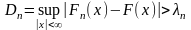. (20.3)

А.Н.Колмогоров доказал, что в случае справедливости гипотезы Н₀ распределение статистики D_n не зависит от функции F(x), и при

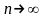
где 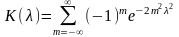- (20.4)

- критерий Колмогорова, значения которого можно найти в соответствующих таблицах. Критическое значение критерия λ_п(α) вычисляется по заданному уровню значимости α как корень уравнения .

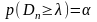Можно показать, что приближенное значение вычисляется по формуле

,

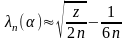где z – корень уравнения

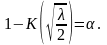
На практике для вычисления значения статистики D_n используется то, что

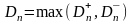, где

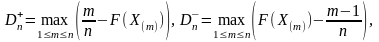
а 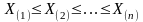- вариационный ряд, построенный по выборке Х₁, Х₂, …, Х_п.

Можно дать следующее геометрическое истолкование критерия Колмогорова: если изобразить на плоскости Оху графики функций F_n(x), F_n(x) ±λ_n(α) (рис. 1), то гипотеза Н₀ верна, если график функции F(x) не выходит за пределы области, лежащей между графиками функций F_n(x) -λ_n(α) и F_n(x) +λ_n(α).

х