1.Основные задачи эконометрики. Эконометрические модели. Примеры.

Эконометрика – это наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей.

К задачам эконометрики относят:

1. обнаружения и анализ статистических закономерностей в экономике

2. построение на базе выявленных эмпирических зависимостей эконометрических моделей

3. разработка методов оценки параметров модели

4. уточнение или отклонение гипотезы о существовании связи между экономическими показателями

Эконометрическая модель – это упрощенное, формальное описание экономической системы, представляющей собой экономические объекты, их свойства, экономические явления и процессы.

Классификация эконометрических моделей

1. регрессионная модель с одним уравнением y=f(x1….xm,E)

У- зависимая, обхъясняемая переменная (эндогенная, результативная)

Xm-независимая, объясняющая переменная фактороные

E Случайная величина

Если m=1 – парная однофакторная

Если m>=2 множественная регрессия или многофакторная

В зависимости от видов функции: линейные, нелинейные

Парная линейная регрессия y=α+βx+E

Парная нелинейная регрессия y=αx^βE (степенная)

2. Модели временных рядов (составляется из нескольких компонентов)

T(t)-тренд, тенденция (длит сохр. Изменения в некот. Направлении)

Пример: употребление электроэнергии возрастает ( возрастает тренд)

S(t)-сезонность (описывает повтор. Эк. Процессов в теч. Небол. Промежутков времени до 1 года

Пример: поток клиентов в магазине

C(t)-циклич. Компоненты ( описывают повторение процессов в течении длительного времени более 1 года)

Пример: нужно иметь наблюдения за неск лет

E- Случайная составляющая – есть в модели всегда если модель экономическая

3. Мультипликативная модель

Y=T(t)S(t)*E

4. Аддитивная модель Y=T(t)+S(t)+E

2. Классификация переменных. Типы данных.

Классификация переменных:

1. Эндогенные переменные (внутренние) –переменные, значение которых формируются внутри модели под влиянием экзогенных и эндогенных переменных.

2. Экзогенные переменные- те значения, которые формируются вне модели до некоторой степени они планируемы и управляемы.

3. Лаговые переменные- переменные построены по данным временных рядов для которых значениях взяты в предыд. По отношению к текущему моменту времени, т.е. с некоторым смещением (лагом)

4. Предопределенные переменные – те значения, которые к текущему моменту времени уже известны. К ним относятся все экзогенные переменные и лаговые эндогенные переменные.

5. Фиктивные переменные – количественным образом описывают качественные показатели. Пример качественного показателя : уровень образования.

Типы данных:

1)пространственная выборка - статистические данные эконометрического показателя собранные для разных однотипных объектов примерно в равных условиях в один и тот же момент времени (Прибыль 10 фирм производящие машины за март 2005)

2)временные ряды – статистические данные эконометрического показателя собранные для одного и того же объекта в последующие моменты времени через равные интервалы (прибыль ежемесячная компания производит машины за 2005)

3)панельные данные - статистические данные эконометрического показателя собранные для групп однотипных объектов в последовательные моменты времени (прибыль ежемесячная 10 фирм производящие машины на протяжении 2005)

3. Типы данных, измерения в эконометрике

Типы данных:

1)пространственная выборка - статистические данные эконометрического показателя собранные для разных однотипных объектов примерно в равных условиях в один и тот же момент времени (Прибыль 10 фирм производящие машины за март 2005)

2)временные ряды – статистические данные эконометрического показателя собранные для одного и того же объекта в последующие моменты времени через равные интервалы (прибыль ежемесячная компания производит машины за 2005)

3)панельные данные - статистические данные эконометрического показателя собранные для групп однотипных объектов в последовательные моменты времени (прибыль ежемесячная 10 фирм производящие машины на протяжении 2005)

Измерения в эконометрике

Измерение показателя- это регистрация у объекта уровня проявления некоторого свойства.

Сущ.3типа измерений:

1.связан со сравнением объектов, которые тождественны или отличны друг от друга по какому-либо свойству, либо они одинаковые, либо разные

2.Предполагает сравнение объектов по интенсивности проявления свойства. Количественное различие между отдельными гражданами не регист.

3.Сравнение с эталоном. Все показатели значимости кот. Регистрируются (качественные, количественные)

Для измерения качеств. показателей сущ 2 шкалы

1)Номинальная (измерение в этой шкале явл классификацией). На этой шкале столько числовых значений, сколько классов м.б. выделено. Числа играют роль меток и никакие операции с числами в этой шкале вып.нельзя.Шкала дискретна.(пр.признак-пол:муж,жен)

2)ординальная ( порядковая)измерения в этой шкале предполагает установление различий не только какому-либо свойству, но и по уровню его проявления. Объекты упорядочиваются, сравнение в этой шкале имеет смысл, а количеств.различие-нет.(пр.образование-начальное,среднее,высшее)

4. Основные этапы эконометрического моделирования. Пояснить на примере

1 этап- априорный- описание экон. модели..На этом этапе строится эк. модель, определяются конечные цели моделирования. Для этого определяется набор участвующих в модели показателей, устанавливаются, какие из переменных рассматриваются как эндогенные, а какие как экзогенные и лаговые эндогенные. Также осуществляется предварительный анализ сущности изучаемого явления и формализации априорной информации об экономических предпосылках моделируемого явления

Пример:Владелец автосалона по продаже поддерженных автомобилей

y- цена авто;х1-срок эксплуатации;х2-пробег;х3-объем двигателя;х4-состояние авто

2этап – построение эконометрической модели, выбирается спецификация, т.е. осуществляется построение эконометрической модели в такой форме , которую можно оценить с пом. доступных статистических данных. Иногда удаются построить несколько эконометрических моделей на основе одной экономической,, отличающихся видами функциональной формы уравнений, предположениями о распределении случайных членов и составом входящих факторов.

1.определить какие из собранных показателей войдут в модель

2.Вид функциональной связи(y-объем производ. Прод.;К-затраты капитала;

L-затраты труда;Е - случайная величина;K,L- независимые переменные(экзогенные)

Y=A*K^α * L^b *E

3 Этап Тестирование спецификации модели и проверка гипотез

R выбираем тот метод, который подходит для вычисления оценок параметров. Каждый метод требует проверки определенных условий для возможности его применения. Если оценки противоречат экономическим оценкам, в полученном результате необходимо найти объяснения либо скорректировать модели или собрать данную информацию.

4Этап – Верификация модели

Выполняется сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных. Если модель адекватна экономическому явлению и имеет приемлемую точность, то на ее основе проводится анализ моделируемой системы и строится прогноз- точечный или интервальный.

5. Классификация эконометрических моделей.

1. регрессионная модель с одним уравнением y=f(x1….xm,E)

У- зависимая, обхъясняемая переменная (эндогенная, результативная)

Xm-независимая, объясняющая переменная фактороные

E Случайная величина

Если m=1 – парная однофакторная

Если m>=2 множественная регрессия или многофакторная

В зависимости от видов функции: линейные, нелинейные

Парная линейная регрессия y=α+βx+E

Парная нелинейная регрессия y=αx^βE (степенная)

2. Модели временных рядов (составляется из нескольких компонентов)

T(t)-тренд, тенденция (длит сохр. Изменения в некот. Направлении)

Пример: употребление электроэнергии возрастает ( возрастает тренд)

S(t)-сезонность (описывает повтор. Эк. Процессов в теч. Небол. Промежутков времени до 1 года

Пример: поток клиентов в магазине

C(t)-циклич. Компоненты ( описывают повторение процессов в течении длительного времени более 1 года)

Пример: нужно иметь наблюдения за неск лет

E- Случайная составляющая – есть в модели всегда если модель экономическая

3. Мультипликативная модель

Y=T(t)S(t)*E

4. Аддитивная модель Y=T(t)+S(t)+E

6.Задачи регрессионного анализа. Виды зависимостей между переменными.

Задачами регрессионного анализа являются установление формы зависимости между переменными, оценка функции регрессии, оценка неизвестных значений (прогноз значений) зависимой переменной.

Между переменными существуют зависимости такие как:

1)Функциональная зависимость – когда каждому значению переменной х соотв. Единственное значение переменной у. (например скорость свободного падения в вакууме в зависимости от времени)

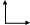
2)Статистическая зависимость-зависимость, при которой каждому значению одной переменной соответствует набор возможных значений другой переменной. Этот набор называется условием распределения (например Зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности)

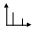
3. Корреляционная зависимость – функциональная зависимость построенная на основе статистических данных. Когда каждому значению одной переменной ставится условие мат. Ожидания др.

7. Способы оценивания. Свойства оценок.

Различают оценки точечные и интервальные. Точечная оценка θ* параметра θ – это числовое значение этого параметра, полученное по выборке объема n. Нужно следить за терминами, делая важное различие между способами или формулой оценивая и рассчитанным по ней для данной выборки числом, являющимся значением оценки.

Способ оценивания- это общее правило, или формула, в то время как значение оценки – это конкретное число, которое меняется от выборки к выборки.

Генеральная совокупность – множество всех возможных значений или реализаций исследуемой случайной величины Х при данном комплексе условий.

Выборка – часть генеральной совокупности, отобранная для изучения.

Для нахождения генеральных числовых характеристик необходим анализ всей генеральной совокупности. В реальности работают с выборками и находят оценки генеральных характеристик: выборочное среднее, выборочную дисперсию , выборочное среднее квадратическое отклонение .

Свойства оценок

1. несмещенность

2. эффективность

3. состоятельность

1.θ* оценка параметра θ несмещенные , если ее мат ожидание = параметру

2.θ* параметра θ называется эффективной оценкой, если ее дисперсия любой другой альтернативной оценки, при использовании одного и того же объема наблюдения n наименьшая

3.оценка θ* называется состоятельной, если при увеличении объема выборки до бесконечности она сходится к оценив. Параметру по вероятности

Для состоятельности оценки при увеличении объема выборки ее дисперсия уменьшается. Для двух состоятельных оценок, обычно справедливо, что дисперсия < у той оценки, для расчета которой используется большее число наблюдений, но при этом нельзя говорить , что она эффективнее. Эффективность с помощью дисперсии только при условии, что объем выборок одинаковый.

8. Проверка статистических гипотез

Статистическая гипотеза- любое утверждение о виде или параметре неизвестного закона распределения. Основная гипотеза, которая подлежит проверке.

Выдвигается гипотеза Н₁, Н_0. Выбор критерий проверки распределения известно, значение рассчитывается по выборке. По таблице находим критическое значение. Нужно знать α и число степеней свободы. α-ошибка первого рода. Рассчитанное значение сравнивается с критерием и делается вывод. Если расчетное значение > критического, то возможно 2 варианта рассуждения

1.считаем, что в единичном испытании маловероятное событие, отклоняем гипотезу Н₀

2.считаем, что произошло редкое событие и продолжаем быть уверенными, что Н₀ верна

9.Парная регрессия. Общее описание МНК

Регрессия – односторонняя вероятностная зависимость случайной переменной Y от одной (или нескольких) независимой переменной X . Величины X рассматриваются как неслучайные независимо от их истинного закона распределения.

Парная регрессия

Условное математическое ожидание случайной величины Y есть функция от X , которая называется функцией регрессии:

M(Y X ) = f (x)

Для описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная X примет значение x. Реальные значения зависимой переменной не всегда совпадают с ее условными математическими ожиданиями и могут быть различными при одном и том же значении объясняющей переменной.

В регрессионное уравнение включают случайное слагаемое ε , которое указывает на стохастический характер зависимой переменной Y

Y = M(Y X ) +ε

Причины существования случайной составляющей:

1. Не включение всех объясняющих переменных.

2. Агрегирование переменных.

3. Выборочный характер исходных данных.

4. Неправильная функциональная спецификация.

5. Возможные ошибки измерения.

Метод наименьших квадратов Оценка параметров уравнения осуществляется МНК. В основе лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметра модели, при котором минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по уравнению регрессии.

S=∑ (Y_I – Y(X))²→MIN

Система уравнений для нахождения параметров линейной парной регрессии с помощью МНК имеет след. вид:

N*A₀ + A₁*∑X = ∑Y

A₀*∑X+A₁*∑X²=∑X*Y (2.3)

N- объём исследуемой совокупности.

А₀ - среднее влияние на результативный признак неучтённых факторов.

А₁ (А₂) – коэффициент регрессии, показывает на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу в его собственном измерении.

Если связь между признаками криволинейная и описывается уравнением параболы, то система нормальных уравнений будет иметь следующий вид:

N*A₀ + A₁*∑X + A₂*∑X² = ∑Y,

A₀*∑X+A₁*∑X²+A₂*∑X³=∑XYA₀*∑X²+A₁*∑X³+A₂*∑X⁴= ∑X²Y (2.4)Оценка обратной зависимости между Х и У осуществляется на основе уравнения гиперболы. Тогда система нормальных уравнений выглядит так: N*A₀ + A₁*∑1/X = ∑X

A₀*∑1/X + A₁∑1/X² = ∑Y/X

10. Вывод формул для оценок параметров парной линейной регрессии.

Точечные оценки параметров находим по методу наименьших квадратов.

b= a= -b

Для параметров проверяем их статистическую значимость. Выдвигаем гипотезы

Но- параметр β- незначимый β=0

Н1-параметр β- значимый β неравно 0

Tb=(b-β)/Sb β=0

Sb=Socт/Sx¬n

Tкр (α, n-2)

Tb<tкр выбираем Ho

Ho – параметр α незначимый α=0

H1 – параметр α значимый α не равно 0

Ta=(a-α)/Sa

Sa=(Sост/Sx¬n)*¬x^2-

Tкр (α, n-2)

Ta<tкр выбираем Ho

Строим доверительный интервал

b-β<tкр

-tкр<(b-β)/Sb<tкр

β принадлежит (b-tкрSb; b+tкрSb)

С помощью интервалов можно проверить стандартные и нестандартные гипотезы.

Для стандартной гипотезы: если границы интервала одного знака , то параметр значимый, границы разного знака параметр не значимый

11. Дисперсионный анализ. Оценка значимости уравнения регрессии

Дисперсионный анализ используется для проверки значимости уравнения в целом.

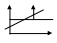AC=AB+BC

Yi-y^=yi-yi^+yi^-y^

Суммируем по всем наблюдениям и возводим в квадрат

Σ(yi-y^ )²=Σ(yi-yi^)² +Σ(yi^-y^)²

2E(YI-YI^)(yi^-y^)=0

E(yi-yi^)yi^-E(yi-yi^)y^- =Eei(a+bxi)- y^- Eei=aEei(yi-yi^)xi

По методу наименьших квадратов мы получаем систему уравнения для вычисления сделок

E(yi-yi^)(-xi)=0

E(yi- y^- )² -полная сумма квадратных отклонений

E (yi-yi^) остаточное или необъясненное число регрессии

n-2 – число степеней свободы

n-2=n-k=n-m-1

E(yi^- y^- ) ² -факторная

К- число оцениваемых параметров

К=2 (α,β) для парной регрессии

m-число объясняющих переменных в модели

m=k-1

Ho-уравнение не значимое

H1-уравнение значимое

Dфакт <=D ост

Dфакт >D ост

F=-S²фак/S²ост

F=(E(yi^- y^{- )2} / E(yi- yi^ ^{)2 )*} (n-2)

Fкр(α,1, n-2)

F>Fкр –Н1 знач.

F<Fкр-Но незнач.

12.Коэффициент парной корреляции, коэффициент детерминации, диапазон их изменения. Интерпретация значений диапазона.

Коэффициент парной корреляции хар-ет тесноту и напр-е линейной связи

r_xy =Sxy/SxSy=(х_ср.у-ху_ср)/√( х²_ср - х _ср² )√у² _ср - у _ср ² )

r_xy →1-связь тесная. r_xy →0-связть отсутствует

Rxy= r_xy² - только для парной регрессии

Коэффициент детерминации

R² =∑(ŷi-y_ср) ² / ∑(yi-y_ср ) ²

1-R² –доля влияния неучтенных факторов

1-R² =∑(уi-yi^₎ ² / ∑(yi-y_ср ) ²

13.Проверка гипотез относительно параметров линейного уравнения парной регрессии.

Точечные оценки параметров находятся по методу наименьших квадратов:

b= a= -b

Точечные оценки не совпадают со значением парам-в.Для парам-в мы проверяем их статистическую зач-ть.стандартные гипотезы.Н₀:парам-р β незнач-й;H₁:парам-р β знач.β=0;tb= ;Sb=t_кр(α,n-2);|tb|<t_kr=>H_0.;|tb|>t_kr=>H_1.;эти гипотезы,эквив-ны,гипотезам о знач-ти ур-ия в целом.|tb|= .Стандартная гипотеза для параметра α.Н₀ парм-р αнезнач.α=0;Н₁пара-р знач.α≠0;t_a= t_kr(α,n-2);|ta|<t_kr=>H₀;|ta|<t_kr=>H₁;знач.ур-ия со своб-м членом не связано.нестанд.гипотезы :H₀:β=β* ;H₁:β≠β*;(β*-изв.числов.знач.);tb= ;для пар-ра α нестанд-ая гипотеза формулир-ся аналогично.Довер-ые интервалы.P(|tb|<t_kr)=1-α= ;| |<t_kr;-t_kr< .;β€(b-t_krSb,b+t_krSb);довер-й интервал строится аналогично,с помочью довер-го интнр-ла можно проверить станд. И нестанд. Гипотезы.Для станд-х если гипотезы 1 знака параметр знач-й.если разного знака параметр незнач-й. если β*€ интервалу то верно Н₀параметр может принимать это знач-ие.Если β* интервалу то верна гипотеза Н_1.

14.Интервальные оценки параметров линейного уравнения парной регрессии.

Интервальной оценкой параметра Q называется числовой интервал, который с заданной вероятностью γ накрывает неизвестное значение параметра Q

Такой интервал называется доверительным. γ-доверительная вероятность.

1-α , где α-вероятность того, что построенный интервал не вкл. Параметр.

Длина интервала зависит от объема выборки n и доверительной вероятности. Чем больше доверительная вероятность, тем интервал больше, Чем больше объем выборки , тем интервал меньше (разброс, дисперсия меньше)

15.Вычисление предсказываемых значений зависимой переменной. Доверительные интервалы для предсказаний. Коэффициент эластичности.

Значение объясняющих переменных для прогноза обозначается Хр, если Хр принадл.(Хmin;Xmax). Прогнозирование представляет собой интерполяцию.

Хр<Xmin или Xp>Xmax экстрополяция

Для получения адекватного прогноза Хр<Xmin-1\3(Xmax-Xmin)

Xp<Xmax+1\3(Xmax-Xmin)

Не должно быть отклонения больше чем на треть.

Точечный прогноз находится по оцененной модели

Ŷр=a+bxp-доп.интерв.прогноз Ур принадл.(ŷр-Syptкр; ŷр+ Syptкр)

Syp^=Socт√1+1/n+(x_p-x_cp)² /n*Sx²

Xp→Xcp Syp→наим.

Отклонения д.б. наим.

Коэффициент эластичности

Показывает на ск. % в среднем изменяется У при увеличении Х на 1%

Ех=у’x*x/y

Ŷ=a+bx→Ex=bx/a+bx

Ŷ=a+b/x→Ex=-b/ax+b

Ŷ=ax²→Ex=b

Ŷ=ab^x →Ex=xlnb

16. Выбор функции. Сравнение различных моделей.

Существует 2 подхода:

1.содержательный анализ

2.формальный анализ

Содержательный анализ основан на экономических предпосылках рассматриваемой модели.

Формальный анализ основан на преобразованиях, которые позволяют предпочесть некоторую модель всем остальным.

Модели. В которых зависимая y представляют в одной и той же функциональной форме, можно сравнить с помощью коэффициентов детерминации R²

Предпочтение отдается той моделе, у которой соответствующий коэффициент больше.

Для моделей, в которой используется разные функциональные формы для зависимой переменной y , непоср. Ср-ть R2 сущ. Больше, чем др., то выбор в моделе с большим коэффициентом.

Если значение коэффициента детерминации для разных форм модели близки друг к другу в этом случае нужно воспользоваться специальные процентные ставки.

Преобразование Бокса-Кокса позволяет сравнить с использованием у и lny. Сравнение суммы квадратов отклонения линейной и логарифмической моделей.

1.вычисляется среднее геометрическое значение у в выборке. Оно совпадает с экспонентой средне арифметической

2.Пересчитывает наблюдение у, они делятся на это значение

3.Рассчитываются новые переменные при значении от 1 до 0

4.рассчитывается регрессия для новых переменных при значении от 1 до 0

Плавно изменение в указ. Интервале устанавливается значение для кот. Сумма квадратных остатков минимальна, выбирает то, которое ближе т. min

17.Основные предпосылки регрессионного анализа (условия Гаусса-Маркова)

1.регрессионная модель линейна по параметрам, корректно специфицирована и содержит аддитивный случайный член

Yi=α+βxi+Ɛi

2.случайный член имеет нулевое среднее значение. Мат.ожидание для случайного отклонения равно нулю для всех наблюдений.

М(Ɛi)=0

3.Дисперсия случайных отклонений постоянна. Выполнение этого условия-гомоскедастичность)

D(Ɛi)=D(Ɛj)=σ²

4.Значения случайного члена распределены независимо друг от друга

Cov(Ɛi;Ɛj)=0

5.Случайный член независим от объясняющих переменных

Cov(xi,Ɛi)=0

18.Нелинейная регрессия. Виды нелинейной регрессии.

Классы нелинейных регрессий:

1)Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам.

Например:

Y=α+βx+λx²+Ɛ-полином второй степени

Такие регрессии могут быть линеаризованы простой заменой переменных.x=x1,x²=x2

2)регрессии, нелинейные по оцениваемым параметрам.

Например:

У=α*х^β*Ɛ-степенная модель

Уравнения этой группы можно разбить на 2 подгруппы:

-нелинейные модели внутренне линейные-степенная(линеаризуются с пом.логарифмирования)

-нелинейные модели внутренне нелинейные-показательная(невозможно преобразовать)

19.Преобразование случайного члена в модели нелинейной регрессии

Случайный член в преобразованном уравнении должен участвовать в виде слагаемого и удовлетворять всем условиям Гаусса-Маркова. Иначе полученные по МНК оценки коэффициентов не будут обладать обычными свойствами и проводимые для них тесты дадут недостоверную информацию. Для применения t и F критериев необходимо, чтобы выполнялось предположение о нормальности распределения случайного члена линейного уравнения регрессии. Но так как преобразование нелинейных моделей внутренне линейных связано с логарифмированием, то в преобразованную модель часто входит логарифм случайного члена lnƐ, который и должен иметь нормальное распределение. Тогда случайное отклонение Ɛ должно быть распределено нормально. Уравнение нелинейной регрессии дополняется показателем тесноты связи. В данном случае это показатель корреляции:

Rxy=√∑(y^-ӯ)²/ ∑(y-ӯ)²

20.Общая модель множественной линейной регрессии. Основные предположения регрессионного анализа.

Модель множественной линейной регрессии:

Y=βo+β1X1+β2X2+…βmXm+Ɛ

У-фактическое значение результативного признака

Βo-постоянная величина(св.член)

Βj-коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений

Условия Гаусса-Маркова:

1.Спецификация модели:

Y=Xβ+Ɛ

2.Случайный член имеет нулевое среднее значение. Мат.ожидание случ.отклонения равно 0.

М(Ɛi)=0

3.Гомоскедастичность. Дисперсия случ.отклонений Ɛi постоянна.

D(Ɛi)=D(Ɛj)=σ²

4.Отсутствие автокорреляции. Случайные отклонения Ɛi и Ɛj являются независимыми друг от друга для всех i≠j

5.Х-неслучайная матрица имеет максимальный ранг-m+1. Т.е. отсутствие строгой линейной зависимости между объясняющими переменными, т.е. ни один столбец не явл.линейной комбинацией других.

6.Случ.член распределен нормально

22. Дисперсии и стандартные ошибки коэффициентов.

Эмпирические коэффициенты множественной линейной регрессии вектор b определяется по формуле b=(X^TX)^-1 X^TY

Подставляя в это соотношение теоретическое значения Y=Xβ+ε, получим:

b=(X^TX)^-1 X^T (Xβ+ε)= (X^TX)^-1(X^TX)β+(X^TX)^-1 X^Tε=β+ (X^TX)^-1 X^Tε

Следовательно , b-β=(X^TX)^-1 X^Tε

Дисперсионно-ковариационная матрица – вектора оценок параметров:

K(b)=M [(β-b)( β-b)^T]=M[((X^TX)^-1 X^Tε)(( X^TX)^-1 X^Tε)^T]=M[(X^TX)^-1 X^Tεε^TX(X^TX)^-1]

Матрица X – детерминированная, неслучайная

K(b)= (X^TX)^-1 X^TM(εε^T)X(X^TX)^-1=(X^TX)^-1 X^T σ²EX(X^TX)^-1= σ² (X^TX)^-1

На главной диагонали матрицы K(b) находятся дисперсии оценок параметров регрессии:

k_jj=M[(b_j-1-β_j-1) (b_j-1-β_j-1)]=M(b_j-1-β_j-1)²= σ² _bj-1=D(b_j-1),

где j-1,2,….m+1

D(b_j-1)= σ² _bj-1= σ² [(X^TX)^-1 ]_jj

J=1,2,….m+1, где [(X^TX)^-1 ]_jj – диагональный элемент матрицы X^TX

Поскольку истинное значение дисперсии по выборке определить невозможно, оно заменяется соответствующей оценкой

S²_ост= E(y-y^)²/ (n-k)= Ee²/(n-k)

Где k- число оцениваемых параметров модели.

Следовательно, по выборке мы можем определить только выборочные дисперсии для вектора оценок b

S² _bj-1= S²_ост [(X^TX)^-1 ]_jj , j=1,2…m+1

Как и в случае парной регрессии S_ост=­­­­­ ^¬_S2ост ^–называется стандартной ошибкой регрессии, а S _bj=^¬_{S2 bj –стандартной} ошибкой коэффициента регресии

23.Интервальные оценки коэффициентов уравнения множественной линейной регрессии. Проверка статистической значимости коэффициентов.

По аналогии с парной регрессией рассчитываются интервальные оценки параметров βj

β_j( j = 0,1,.. m). Для построения интервальной оценки коэффициента β _j строится t -статистика:

bj - βj

t =

Sbj

имеющая распределение Стьюдента с числом степеней свободы df = n − k ,

где k - число оцениваемых параметров модели. Для построения доверительного интервала коэффициента β_j находится критическое значение t крит (α; df), где α - уровень значимости, вычисляются границы: -tкрит Sbj≤ bj≤ +tкрит Sbj

Статистическая значимость коэффициентов множественной регрессии с m объясняющими переменными проверяется на основе t-статистики:

имеющей в данном случае распределение Стьюдента с числом степеней свободы v = n- m-1. При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точной распределения Стьюдента.

В случае, если то статистическая значимость соответствующего коэффициента множественной регрессии подтверждается. Это означает, что фактор Xj линейно связан с зависимой переменной Y. Если же установлен факт незначимости коэффициента bj, то рекомендуется исключить из уравнения переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.

24.Проверка общего качества уравнения множественной регрессии.

Для этой цели, как и в случае множественной регрессии, используется коэффициент детерминации R²:

Справедливо соотношение 0≤R²≤1. Чем ближе этот коэффициент к единице, тем больше уравнение множественной регрессии объясняет поведение Y.

Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R², так как каждая последующая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной.

Иногда при расчете коэффициента детерминации для получения несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы, т.е. вводится исправленный коэффициент детерминации:

Соотношение может быть представлено в следующем виде:

для m>1. С ростом значения m исравленный коэффициент детерминации растет медленнее, чем обычный. Очевидно, что только при R² = 1. может принимать отрицательные значения.

Доказано, что увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.

После проверки общего качества уравнения регрессии надо провести анализ его статистической значимости. Для этого используется F-статистика:

Показатели F и R² равны или не равны нулю одновременно. Если F=0, то R²=0, следовательно, величина Y линейно не зависит от X1,X2,…,Xm..Расчетное значение F сравнивается с критическим Fкр. Fкр, определяется на основе распределения Фишера. Если F>Fкр, то R2 статистически значим.

25. Коэффициенты детерминации множественной регрессии. Скорректированный коэффициент детерминации.

Величина R² показывает, какая часть (доля) вариации зависимой

переменной обусловлена вариацией объясняющей переменной

R²=Qr/Q=1-(Qe/Q)

Qr,Qe-сумма квадратов, обусловл. Регрессией и остаточной суммой квадратов

Qr=E(y – y) Qe=

чем ближе R^ к единице, тем лучше регрессия описывает зависимость между объясняющими и зависимой переменными. использование только одного коэффициента

детерминации R? для выбора наилучшего уравнения регрессии

может оказаться недостаточным. На практике встречаются случаи,

когда плохо определенная модель регрессии может дать

сравнительно высокий коэффициент R². Недостатком коэффициента детерминации

что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле

предпочтительнее использовать коэффициент детерминации

чем больше число объясняющих переменных

р, тем меньше R^ по сравнению с R . В отличие от R

скорректированный коэффициент может уменьшаться при

введении в модель новых объясняющих переменных, не оказывающих

существенного влияния на зависимую переменную.

26. Ошибки спецификации: невключение существенных переменных.

При отсутствии существенной переменной существенное отклонение может оказаться гетероскедаcтичным. Для V может нарушаться предпосылка об отсутствии автокорреляции. Если между существенными переменными х1,х2 есть связь она будет и между х1 и V. Оценки параметров при существенных переменных оставшихся в модели рассчитывается со смещением. При отсутствии существенных переменных в модели могут нарушаться предпосылки регрессионного анализа: гомоскедастичность, отсутствие автокорреляции.

27. Ошибки спецификации: включение несущественных переменных.

Несущественные переменные- те, которые в этой модели отсутствуют.

Оценки параметров при существенных переменных остаются несущественными.

Однако, за счет несущественных переменных увеличивается число переменных в модели, состоятельность оценок возрастает.

Параметры существенных при существенных переменных из этого могут оказаться статистически незначимыми и уравнение вцелом может оказаться статистически незначимым.

Несущественные по экономическим предпосылкам модели может оказаться статистически значимыми и даже доминировать. Тогда существенные переменные станут статистически незначимыми. В этом случае оценки параметров при существенных переменных в этом случае будут рассчитываться со смещением.

К модели, где есть несущественные переменные, между несущественными переменными могут быть также корреляционные связи. При включении таких переменных в модель нарушаются предпосылки об отсутствии мультиколлинеарности.

30 Спецификация уравнения множественной регрессии.Тест Рамсея

Тест Рамсея.Он опред-т правильность выбора функциональной зависимости.Его возмож-ти очень ограничены.Он опред-тправильность исправления линейной регрессии.В случае если линейная регрессия отвергается какой должна быть не линейная регрессия тест не дает.Н₀:регр.линейная.Н₁:регр.не линейная.

(*)Y=β₀+β₁X₁+β_mX_m+E ;

(**)Y=β₀+β₁X₁+…+β_mX_m+α₂Y^²+α₃Y^³+…+α_pY^^p+v;

Если регр-ия линейная:α₂=α₃=…=α_p=0. у^: у^=b₀+b₁X₁+…+b_m*X_m.

Если регрессия нелинейная:не все α_iодновременно=0.

31.Логарифмические модели. Производственная ф-ция Кобба-Дугласса.Зависимости, исп в банковском анализе.

Степенная модель - модель нелинейная по оцениваемым параметрам, линеаризующ. по активным параметрам.

Y = A * K^α * L^β * ε

Y = β₀K^β1 * L^β2* ε

ln Y = ln β₀ + β₁ ln K + β₂ ln L + ln ε

Y - объем выпуска

K - затраты капитала

L - затраты труда

β₀ - коэф нейтральн технич прогресса

β₁ - коэф эластичн выпуска по кап-лу

β₂ - коэф элачтичн выпуска по труду

ε - влияние эконом обстановки на измен выпуска

β₁ + β₂ - отдача от масштаба

=1 - постоянн; <1 - убывающ; >1 - возраст

Зависимости исп в банковском анализе:

Модель показат нелинейная по параметрам, линеаризующ, преобраз логарифмирование

y_t = y₀ (1+r)^t * ε

y - зависимая; t - объясняющ

y₀(β₀) - первонач объем инвестиций

r - вставка сложных % *

(* у сложных % - база начисл постоянная,у сложных % - переменная база начисл)

ε - влияние эконом ситуации на доходность инвестир

ln Yt - Ln Y₀ + y ln (1+r) + ln ε

32.Обратная модель.Ф-ция Торнквиста, кривая Филлипса.

Обратная модель относ к регрес линейной по оцениваемым параметрам. Линеаризующие преобразования - замена переменной. Модель исп в том случае, если неограниченное увеличение объясн переменной приводит к некоторому пределу.

y = β₀ + β₁/x₁ + ε

x₁→ ∞ => y→β₀

_1. β₀>0

β₁>0

одна из всевозможных эконом интерпритаций

y- себестоимость ед изделия

x-объем производства

β₀- издеожки, связанные с пр-м изделия

β₀*х - переменные издержки, связ с пр-м этого изделия

β_{1 -} пост издержки

постоянные издержки в себестоимости ед изделия стремятся к 0 при неогранич увеличен объема пр-ва

2. β₀>0

β₁<0

х - доход

у - объем потребления некоторого товара

- β₁/β₀ - min доход, при кот начинается потребление указ товара

β₀ - max объем потребления указанного товара

при такой экономич интеграции ур-е задает ф-цию Торнквиста

3. β₀<0

β₁>0 - кривая Филипса

х - уровень безработицы в %

у - темп изменения з/п

х = - β₁/β₀ - естественный ур безработицы, при кот измение з/п не происходит обеспеч равновесие

Сокращ безработицы приводит к смещению рынка труда в пользу работников. Вакансий много - кадров не хватает. Заполнение вакансий возм при условии повыш з/п. Эконом ситуация , способств сокращению безработицы и хар-ся расширением пр-ва, а это возм при низших %ставках, небольшой инфляции, улучшении благосост и увелич спроса. смешение рынка труда в пользу работодателя, вакансий мало - кандидатов много, з/п снижается.

Экономическая ситуация: сокращ пр-ва, уменьшение спроса на продукцию, высокая инфляция и ставки по кредитам.

33.Суть гетероскедастичности (нарушение условия Гаусса-Маркова)

Гетероскедастичность-нарушение предпосылки регрессионного анализа о постоянстве дисперсии случайного отклонения во всех наблюдениях.

Причины гетероскедастичности:

1.в пространственных выборках гетероскедастичность возникает под влиянием эффекта масштаба.

2.во временных рядах гетероскедастичность возникает в случае, если зависимая переменная имеет большой интервал качественно неоднородных значений или высокий темп изменения.

3.в любой модели гетероскедастичность возникает в случае, если качество данных варьируется внутри выборки.

34.Выявление гетероскедастичности(графический анализ, тест ранговой корреляции Спирмена, тест Голдфелда-Квандта)

Тест ранговой корреляции спирмена

Предположим, что дисперсия случайного члена либо увеличивается, либо уменьшается по мере увеличения х, абсолютные величины остатков и значение х будут коррелированны.

Коэффициент ранговой корреляции определяется как

Если предположить. Что коэффициент ранговой корреляции =0, то коэффициент ранговой корреляции имеет нормальное распределение, мат ожидание=0, дисперсия =1/(n-1)

При использование двустороннего критерия нулевая гипотеза об отсутствии гетероскедастичности будет отклонена при уравнение значимости в 5 %, если она не превысит 1,96% и уравнение значимости в 1 %, если она не превышает 2,58

Тест Голдфелда Квандта.

Применяется, когда есть предположение о прямой зависимости дисперсии ошибки от величины некоторой независимой переменной.Процедура теста:

1.упорядочить данные по убыванию той независимой переменной, относительно которой есть подозрения на гетероскедастичность.

2.исключить d средних наблюдений(d=четверти общего количества наблюдений)

3.построить две независимые регрессии первых (n/2-d/2)=р наблюдений и последних (n/2-d/2) наблюдений и найти соответсвующие остатки для каждой регрессии е1 и е2-вектора, компоненты которых остатки в каждом наблюдении.

4.составить F статистику

35.Устранение гетероскедастичности.Метод взвешенных наим.квадратов.

Для устранения автокорреляции применяют взвешенный метод наименьших квадратов, который является частным случаем обобщенного метода наименьших квадратов. Этот метод обычно применяется, когда дисперсия остатков неоднородна при различных значениях независимых переменных. Можно использовать веса, равные единица на дисперсию остатков и вычислить оценки по методу взвешенных наименьших квадратов. (На практике эти дисперсии обычно не известны, однако они часто пропорциональны значениям независимых переменных, и это пропорциональность может быть использована для вычисления подходящих весов наблюдений).

36. Автокорреляция случайных ошибок.

Автокорреляция определяется как корреляция между наблюд. Показывает автокорреляцию остатков обычно встречается в регрессионном анализе при использовании временных рядов.

Автокорреляция случайных отклонений – нарушение предпосылки регрессионного анализа о независимости случайных возмущений для каждого наблюдения. Чаще встречается положительная автокорреляция, и в моделях временных рядов. Обычно положительная автокорреляция вызывается неучтенными в модели факторами. ( потребление электроэнергии в зимнее время года)

Виды автокорреляции:

1. Чистая (истинная) вызывается зависимостью случ. Члена от знач.

1. автокорреляция 1 порядка

2. автокорреляция 2 порядка

3. автокорреляция высших порядков

2. Ложная автокорреляция вызывается неправильной спецификацией модели.

Последствия истинной автокорреляции:

1. Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными

2. Дисперсия оценок являются смещенными, tстатистика оценок увеличив., и незнач переменная может быть знач.

37.Выявление автокорреляции (графическ анализ, метод рядов,статистика Дарбина-Уотсона)

Методы:

1.Графический анализ - это построение графика зависимостей остатков от времени и визуальное определение наличия автокорреляции остатков.

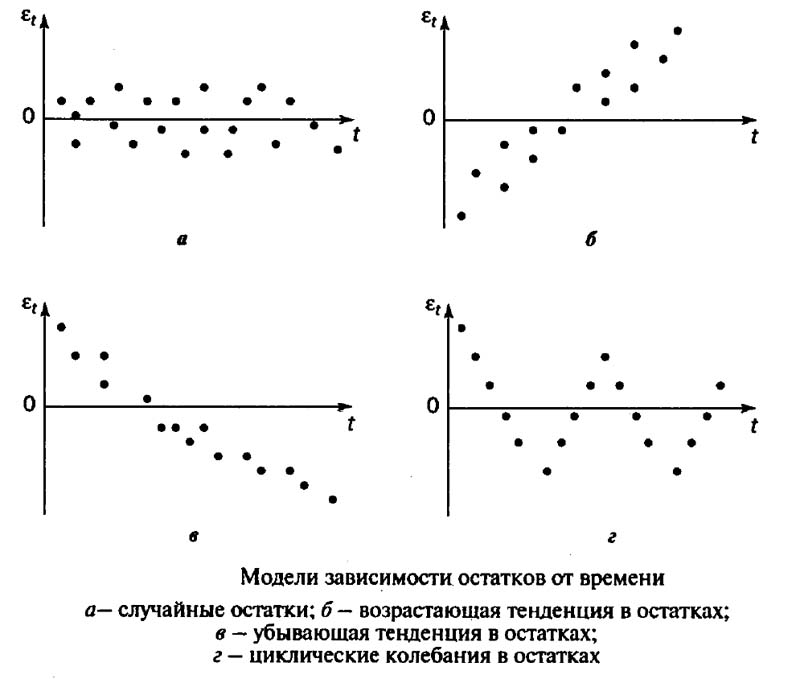
2. Для обнаружения автокорреляции первого порядка можно использовать статистику Дарбина-Уотсона. Статистика Дарбина-Уотсона не предназначена для обнаружения других видов автокорреляции. Используется только для уравнений включающих свободный член. Предполагается, что случайные отклонения определяются по итерационной схеме ε = ρε_t-1 +ν_t и статистические данные имеют одинаковую периодичность (пропуски в наблюдениях отсутствуют).

Общая схема критерия Дарбина-Уотсона следующая:

1. По построенному эмпирическому уравнению регрессии y ˆ _t = b₀ + b₁x_t1 + b₂x_t2 + ... + b_mx_m

определяются значения отклонений e_t = y_t − y ˆ_t для каждого наблюдения t , t =1,K, T .

2. Рассчитывается статистика Дарбина-Уотсона:

T

Σ (e_t - e_t-1)²

t=2

DW =

T

Σ e_t²

t=1

3. По таблице критических точек Дарбина-Уотсона определяются два числа dl и du и осуществляются выводы по правилу:

0 ≤ DW < dl - существует положительная автокорреляция,

dl ≤ DW < du - вывод о наличии автокорреляции неопределен;

du ≤ DW < 4 − du - автокорреляция отсутствует;

4 − du ≤ DW < 4 − dl - вывод о наличии автокорреляции неопределен;

4 − dl ≤ DW ≤ 4 - существует отрицательная автокорреляция.

При больших n выполняется соотношение: Σ e_i² ≈ Σ e_i-1² тогда

2 (Σ e_i² - Σe_i e_i-1)

DW ≈ = 2 (1 - r_eiei-1)

Σ e_i²

Из формулы получаем, что если e_i ≈ e_i-1 , то r_eiei-1≈ 1 (положительная корреляция) и DW ≈ 0,

e_i ≈ − e_i-1, то r_eiei-1≈ − 1 (отрицательная корреляция) и DW ≈ 4. Таким образом, статистика Дарбина-Уотсона может принимать значения из отрезка [0, 4] и согласно схеме показывает наличие или отсутствие автокорреляции.

38. Методы устранения автокорреляции.

1. если автокорреляция ложная, то устранение автокорреляции связано с изменением спецификации

2. построить по данным модель временных рядов

3. использование авторегрессионных схем

Авторегрессионная схема 1 порядка

Если в модели была автокорреляция только 1 порядка, то - случайное отклонение, доля которого предпо. Об отсутствии автокорреляции выполняется

При преобразовании данных теряется 1 наблюдение.

39.Мультиколлинеарность как проблема данных. Следствия мультиколлинеарности

Строгая мультиколлинеарность-наличие линейной функциональной связи между независимыми переменными.

Нестрогая мультиколлинеарность-наличие сильной линейной корреляционной свзят между независимыми переменными

Следствия мультиколлинеарности:

Оценки коэффициентов имеют большие стандартные ошибки, малую значимость, что расширяет доверительные интервалы и делает оценку истинных значений параметров и их влияния на зависимую переменную затруднительной.

Оценки коэффициентов имеют неправильные знаки или неоправдвнно большие значения.

Оценки коэффициентов становятся неустойчивыми и малейшее изменение в выборкемогут привести к существенным изменениями оценок и смене знака.

40.Способы выявления мультиколлинеарности. Частная корреляция

Способы выявления мультиколлинеарности:

1. Высокий R2, но большинство коэффициентов-незначимые.

2.Высокие парные коэффициенты корреляции

3.Высокие частные коэффициенты корреляции

4.Высокие значения коэффициента VIF для βj, свидетельствуют о зависимости переменной Xj от других объясняющих переменных моделей.

Частный коэффициент корреляции-это коэффициент корреляции, очищенный от влияния других переменных.

Процедура получения частных коэффициентов корреляции:

Имеется регрессионная модель: Y=βo+β1X1+β2X2+Ɛ

Определение корреляции между У и Х1 при исключении влияния переменной Х2.

1.Оценим регрессию У на Х2: У=αо+α2Х2, получим Ῡ=ао+а2Х2

2.Оценим регрессию Х1 на Х2: Х1=γо+γ2Х2, получим Х1^=со+с2Х2

3.Удалим влияние Х2, взяв остатки е_у=у-ŷ и е_х1=х1-х1^

41. Пути решения проблемы мультиколлинеарности

1.изменить или увеличить выборку. Увеличение количества данных сокращает дисперсии коэффициентов и увеличивает их значимость. Но увеличение выборки может привести к увеличению автокорреляции

2.исключить одну или несколько переменных. Это может уменьшить мультиколлинеарность, но есть риск получить неверную спецификацию модели

3.Преобразовать мультиколлинеарные переменные

-использовать нелинейные формы

-использовать агрегаты(лин.комбинации нескольких переменных)

-использовать первые разности вместо самих переменных

42.Фиктивные переменные

В регрессионную модель кроме количественных объясняющих переменных часто включат качественные переменные, имеющие несколько уровней градации. Напр., пол(муж,жен). Чтобы включить качественные факторы в модель их значениям д.б.присвоены цифровые метки. Т.О., сконструированные переменные называются фиктивными. Фиктивность переменных-свойство выражать качественный признак количественным образом.

В качестве фиктивных переменных используют обычно бинарные переменные, которые принимают два значения – 0(фактор не действует); 1(фактор действует)

D= сис-ма-0,-работник мужчина; 1-работник женщина.

Т.е. переменная D выражает количественно признак пол.

Модель зависимости з\п от стажа и пола:

Y=βo+β1X1+γD+Ɛ

Сущ.условие: если качественная переменная имеет k альтернативных значений, то при моделировании используется k-1 фиктивных переменных.

43.Тест Чоу

Статистический тест, позволяющий оценить значимость улучшения регрессионной модели после разделения исходной выборки на части. Одним из ограничений линейной регрессии является то, что для различных интервалов значений независимой переменной характер ее связи с выходной переменной может меняться. Например, с увеличением возраста клиента его кредитный рейтинг может возрастать, но до определенного порога (например 50–55 лет), после которого люди начинают чаще болеть, им сложнее найти работу и т.д. Они становятся менее привлекательны для банка в качестве заемщиков и для них имеет место обратная тенденция.Очевидно, что любая модель, которая аппроксимирует такую закономерность единственной линейной зависимостью, вряд ли будет точной. Выходом из ситуации является разделение диапазона значений входной переменной на два, в пределах каждого из которых зависимость между ней и выходной переменной монотонна. Затем для каждого из полученных интервалов строится свое уравнение регрессии. Возникает вопрос: как разделить исходное множество так, чтобы обеспечить лучшую аппроксимацию? Для этого обычно строят множество разбиений, для каждого определяют значимость улучшения модели и выбирают то из них, для которого она максимальна. Для ее оценки и используется тест Чоу, который применяет статистику:

,

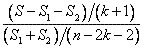где S – сумма квадратов остатков линейной регрессии целой модели, S₁ – сумма квадратов остатков модели, построенной для первого подмножества, S₂ - сумма квадратов остатков модели, построенной для второго подмножества, n – общее число наблюдений выборки. Полученная статистика подчиняется F-распределению Фишера с k+1 и n-2k+1 степенями свободы и используется для оценки значимости улучшения модели при разделении выборки на две части.

44.Система одновременных уравнений (экзогенные, эндогенные, лаговые) переменные. Экономически значимые примеры систем одновременных переменных.

Ряд экономических процессов моделируется не одним, а несколькими уравнениями, содержащими как повторяющиеся, так и собственные переменные. Возникает необходимость использования системы уравнений. В одних уравнениях опред переменная может рассматриваться как объясняющая (независимая), но в тоже время она входит в другое уравнение как зависимая (объясняемая) переменная.

Одна из простейших систем одновременных уравнений проявляется при моделировании спроса-предложения в рыночной экономике. В этом случае, предположение, что спрос Q^D

и предложение Q^S в момент времени t являются линейными функциями от цены P,получаем сис-му:

ф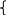 -ция спроса: Q_t^D = b0 + b1p1 + e_t1 , b1<0

ф-ция предл: Q_t^S = b0 + b1p1 + e_t2, b1<0

усл равновесия: Q_t^D = Q_t^S

Наличие случайных отклонений в данных моделях связано с отсутствием в модели ряда важных объясняющих переменных (дохода, цен на ресурсы и т.д.). Изменение одного из этих факторов может отразиться на сдвиге одной или обеих линий. Например, рост дохода потребителей может сдвинуть кривую спроса вверх. Это приводит к нарушению равновесия и равновесного количества.

При рассмотрении систем одновременных уравнений переменные делятся на два больших класса - эндогенные и экзогенные. Эндогенные переменные - переменные, значения которых определяются внутри модели. Экзогенные переменные - это внешние по отношению к модели переменные. Их значения определяются вне модели, потому они считаются фиксированными.

В нашей системе эндогенными переменными будут являться величины спроса, предложения и цены, так как они определяются внутри системы.

Лаговые переменные — экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными.

45 Косвенный метод наименьших квадратов.

Если система уравнений идентифицируемая для оценки ее параметров использ-ся косвенный метод наименьших квадратов.Алгоритм:1.1.от структурной формы переходит к приведенной.1.2.оценивает формы приведенной формы.1.3.выражает оценки параметров в структурной формы через оценки параметров приведенных.

46. Проблемы идентифицируемости.

Ву+Гх=Е –структурная форма

В,Г-матрицы

У-эндогенные переменные

Х- экзогенные переменные

Параметры структурной формы – структурный параметр

1. структурный параметр называется идентифицируемым, если он может быть однозначно оценен с помощью косвенного метода наименьших квадратов

2. структурный параметр называется неидентифицируемым, если его значение невозможно получить. Проблема структуры модели. Неидеен. Не исчезает с ростом количества наблюдений и означает, что сущ. Бесконечное число структурных моделей, имеющих одну и ту же приведенную форму

3. структурный параметр называется сверхидентифицированным, если косвенный метод наименьших квадратов дает несколько различных его оценок. Проблема сверхидентифицирован.- проблема количества наблюдений: с увеличением объема выборки все различные состоятельные оценки параметра стремятся к одному и тому же истинному значению.

47. Трехшаговый метод наименьших квадратов.

Наиболее эффективная процедура оценивания систем регрессионных уравнений сочетает метод одновременного оценивания и метод инстремунт. Переменных. Этот метод называется трехшаговым методом наименьших квадратов.

Он заключается в том, что на первом шаге к исходной модели применяется обобщенный метод наименьших квадратов с целью устранению корреляции случайных членов. Затем к полученным уравнениям применяется двухшаговый метод наименьших квадратов.

Если случайные члены не коррел. Трехшаговый метод сводится к 2хшаговому. Если матрица единичная, то 3хшаговая метод представляет собой процедуру одновременного оценивания уравнения как внешне не связанных.

При достаточно большом числе итерация оценки трехшагового метода наименьших квадратов совпадает с оценками максимального правдоподобия.

48. Понятие экономических рядов динамики. Общий вид мультипликативной и аддитивной модели временного ряда. Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов. Временной ряд (ряд динамики) – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Всякий ряд динамики включает два обязательных элемента: 1.время 2.конкретное значение показателя, или уровень ряда. Ряды динамики различаются по следующим признакам. 1. По времени – моментные и интервальные ряды. Интервальный ряд динамики – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. Таковы, например, ряды показателей объема продукции по месяцам года, количества отработанных человеко-дней по отдельным периодам и т.д. 2. По форме представления уровней – ряды абсолютных, относительных и средних величин, например, потребления продуктов питания на одного члена семьи (кг/год) 3. По расстоянию между датами или интервалам времени выделяют полные и неполные хронологические ряды. Полные ряды динамики имеют место, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Неполные – когда принцип равных интервалов не соблюдается. В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется адитивной моделью временного ряда. Общий вид: Y = T + S + E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Общий вид: Y = T • S • E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (E) и случайной (E) компонент.

49.Моделирование тенденции временного ряда, сезонных и циклических колебаний.

Распространенным способом моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.

Зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:

-линейный тренд: ў_t = a+b·x;

-гипербола: ў_x = a+b/x;

-степенная функция: ў = a·x^b;

-экспоненциальный тренд: ў = e^a+bx (или ў=a·b^x);

Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время x=1,2,...,n, а в качестве зависимой переменной – фактические уровни временного ряда ў_x. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Наиболее простую экономическую интерпретацию имеет линейная функция y = a+bx

а – начальный уровень временного ряда в момент времени x = 0;

b – средний за период абсолютный прирост уровней ряда.

Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени.

Моделирование сезонных колебаний Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели следующий Y = T + S + E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.

Общий вид мультипликативной модели выглядит так:Y = T · S · E Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (E) и случайной (E) компонент.

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений T , S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1.Выравнивание исходного ряда методом скользящей средней.

2.Расчет значений сезонной компоненты S

3.Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (T + E) в аддитивной или (T · E) в мультипликативной модели.

4.Аналитическое выравнивание уровней (T + E) или (T · E) и расчет значений T с использованием полученного уравнения тренда.

5.Расчет полученных по модели значений (T + E) или (T · E).

6.Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи исходного ряда и других временных рядов.

50. Автокорреляционная функция. Ее использование для выявления наличия или отсутствия трендовой и циклической компоненты.

Автокорр-ая функция-это дискретная ф-ия которая представляет собой набор значений коэфф-та автокорр-ии врем-го ряда.r1=rytyt-1;r2=rytyt-2;r3=rytyt-3.При вычислении коэфф-ов автокоррел-ии высоких порядков обьем выборки сокращ-ся обычно старший порядок не превосходит (n /4 в отдель-х случ-х n/2)